[数据结构与算法]二叉树的最近公共祖先

不同于二叉搜索树, 可以根据节点值的大小来判断要找到目标在哪个位置, 需要对每个节点进行左右子树的递归, 具体分析如下

1. 在当前节点的左右两个子树上找到了p,q, 那么就说明该节点就是两节点的最近交叉处, 先画简单点就是这样:

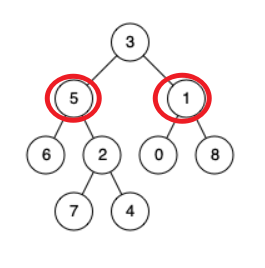
2. 一侧子树返回空, 另一侧子树返回了节点, 那么有以下情况

   1. 返回的是满足p, q均在某一个节点两侧的节点:

      比如找6, 2两个节点, 以3为根节点向左递归找5, 5的左右不为空, 说明5满足, 那么5向上返回, 该返回值作为3单层次的left

      而右子树没有找到q,p, 返回了null, 这是另一侧返回的节点就是找到的结果

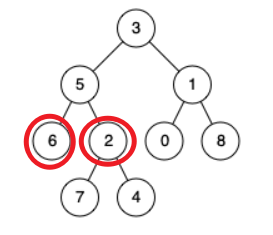
2. 并没有满足, 只是找到了一个值, 如下:
   当前根节点返回的右子树为空, 左子树找到了5即停止了, 并不会向下继续找了,说明另一个节点是在5的子树上, 至于是哪个子树并不重要, 因为最近的只能是5了, 这时返回的5就是正确结果。

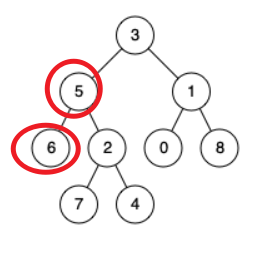
为了便于理解，下面举几个例子作为分析：

1. 由3开始， 左子树递归，递归的最终返回值为left
   1. 到5, 5的左子树递归, 返回值为left
      1. 到6, 6向下递归, left, right都是null, 没找着, 返回null
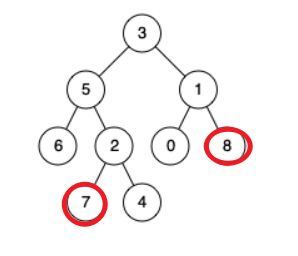
   2. 5右子树递归, 返回值为right
      1. 2左子树递归, 返回值为left, 到7满足, left = 7
      2. 2右子树递归, 没找着, 返回null
      3. 2满足一侧为空, 另一侧不为空, 向上返回找到的节点, 即left
   3. 5满足一侧为空, 另一侧不为空, 向上返回right
2. 3的left不为空, 同理, 右子树找到了8返回给3的不为空
   那么3满足左右均不为空, 向上返回3

代码演示：

const lowestCommonAncestor = (root, p, q) => {
  // 如果root为空, 说明走到头了, 返回空
  // 如果root不为空, 且值等于两节点的任一, 说明找到了目标节点，返回该节点
  if (root === null || p.val ===root.val || q.val === root.val)
  return root
  // 走到这里说明该节点不为空且也不是要找到节点, 那么就左右子树接着找
  // 这里用left和right接收是用于判断是否找到
  // 如果左右都为空, 说明p,q不位于该节点两侧
  // 如果一侧为空,一侧不为空, 按照上述分析的, 可能是找到了正确的节点返回了
  // 也可能是找到了一个节点返回了, 但是终究是找到了一个, 该节点可能是正确节点
  // 也可能只是在当前节点的一侧找到的, 该节点的祖先节点的另一侧可能存在, 总之是需要返回的
  let left = lowestCommonAncestor(root.left, p, q)
  let right = lowestCommonAncestor(root.right, p, q)
  // 该节点左右没找到, 说明不在这里, 返回null
  if (!left && !right) return null
  // 左侧为空, 返回右侧节点, 对于一般节点, 返回的值是说明找到了, 返回上去继续判断
  // 对于根节点, 一侧为空另一侧不为空, 说明返回的这个值就是正确结果(见上述分析第二点)
  else if(!left) return right
  // 同上
  else if (!right) return left
  // 在确定左右都不为空的时候, 说明该节点是正确的, 向上返回
  // 如果是一般节点, 那么向上返回的结果还会做为判断, 因为还要和另一侧对比
  // 结果另一侧为空, 接着返回收到的这个结果继续判断, 直到根节点, 根节点继续判断
  // 一侧为空, 一侧不为空, 那么是最终结果
  
  // 如果是根节点, 那么该值就是最终的正确结果
  return root


}