[数据结构与算法]DDA划线法(Digital Differenttial Analyzer数值微分法)

DDA划线法(Digital Differenttial Analyzer,数值微分法)@TOC

利用计算机画出一条高质量直线
输入：直线两个端点的坐标p0(x0,y0)和p1(x1,x2)
输出：最佳逼近这条直线的像素点集

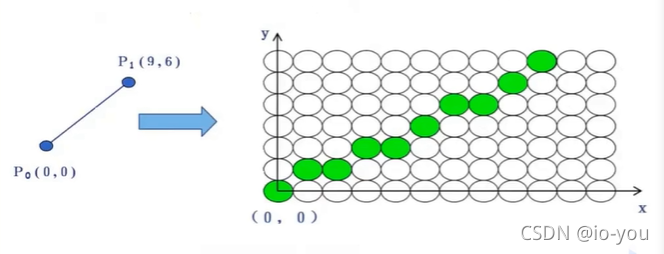
在计算机中这些点集都是离散的，高质量直线的要求应满足
以下三个条件：
（1）直线要直，像素点尽可能靠近理想直线
（2）直线要均匀，连续，点数不能多也不能少
（3）显示线段的速度应该快，不能有卡顿现象（像素点的定位不能用乘除法，要用加减法，而且是正数加减法）

DDA算法是计算机图形学中画直线的基本算法，主要根据直线的斜截方程式（y=kx+b）推导出来的。
假设(|k|<=1)
x(i+1)=xi+1
y(i+1)=yi+k

推导 y0=kx0+b;
x1=x0+1;
y1=k(x0+1)+b=kx0+k+b=y0+k;

最终下一坐标(x,int(y+0.5) //y取整)

假设(|k|>1)
y(i+1)=yi+1;
x(i+1)=xi+1/k

推导 y0=kx0+b;
y1=y0+1;
y0+1=k(x1)+b; x1=(y0+1-b)/k;
x1=x0+1/k;

最终下一坐标(int(x+0.5),y) //x取整)
代码

void CthreeView::OnDraw(CDC* pDC)
{
	CthreeDoc* pDoc = GetDocument();
	ASSERT_VALID(pDoc);
	if (!pDoc)
		return;

	 //TODO: 在此处为本机数据添加绘制代码
	//DDA算法
	int x0 = 100, y0 = 100, x1 = 300, y1 = 200;
	float x, y, i, dx, dy, k;
	dx = (float)(x1 - x0); dy = (float)(y1 - y0);
	k = dy / dx; y = y0; x = x0;
	if (abs(k) < 1)
	{
		for (; x <= x1; x++)
		{
			pDC->SetPixel(x, int(y + 0.5), RGB(255, 0, 0));
			y = y + k;
		}
	}
	if (abs(k) >= 1)
	{
		for (; y <= y1; y++)
		{
			pDC->SetPixel(int(x + 0.5), y, RGB(255, 0, 0));
			x = x + 1 / k;
		}
	}
}