
题目要求找出数组 nums 中乘积最大的连续子数组,最直接的办法是遍历整个数组,穷举以数组元素 nums[i] 为开头的所有连续子数组,通过比较所有连续子数组的乘积,找到最大值,并返回。
可是穷举所有子数组的乘积的过程中,存在很多重复计算。因此可以考虑使用动态规划的思想来优化算法。
知识点: 动态规划及其空间优化
1. 暴力遍历
这种方法通过穷举所有可能的结果,得到最大值。因此要对数组进行两次遍历,并假定数组首元素为乘积最大值 max 。
第一次遍历确定乘积子数组的开头元素 nums[i]
第二次遍历确定子数组的组成长度,子数组范围从开头元素 nums[i] 到 数组结尾 nums[nums.size() - 1] ,使用变量 multi 存储当前数组的乘积,并与最大值 max 比较。
class Solution {
public:
int maxProduct(vector<int>& nums) {
int max = nums[0];
for(int i = 0; i < nums.size(); i++)
{
int multi = 1;
for(int j = i; j < nums.size(); j++)
{
multi = multi * nums[j];
max = max < multi ? multi : max;
}
}
return max;
}
};
2. 动态规划
“动态规划问题一定会具备「最优子结构」,才能通过子问题的最值得到原问题的最值。”
那么本题的最优子结构是什么呢?什么时候子数组的乘积为最大?
2.1 定义子问题
本题的子问题是找到乘积最大的所有元素吗?
不是,因为题目要求的是数组,乘积最大的若干元素可能并不相邻,所以无法构成数组。
本题的子问题应该为以 nums[i] 为结尾的乘积最大子数组。
2.2 状态转移方程
动态规划的核心就是写出状态转移方程,并给出基础条件。
下面我们尝试根据题目要求写出状态转移方程。
什么时候以 nums[i] 为结尾的子数组的乘积为最大?
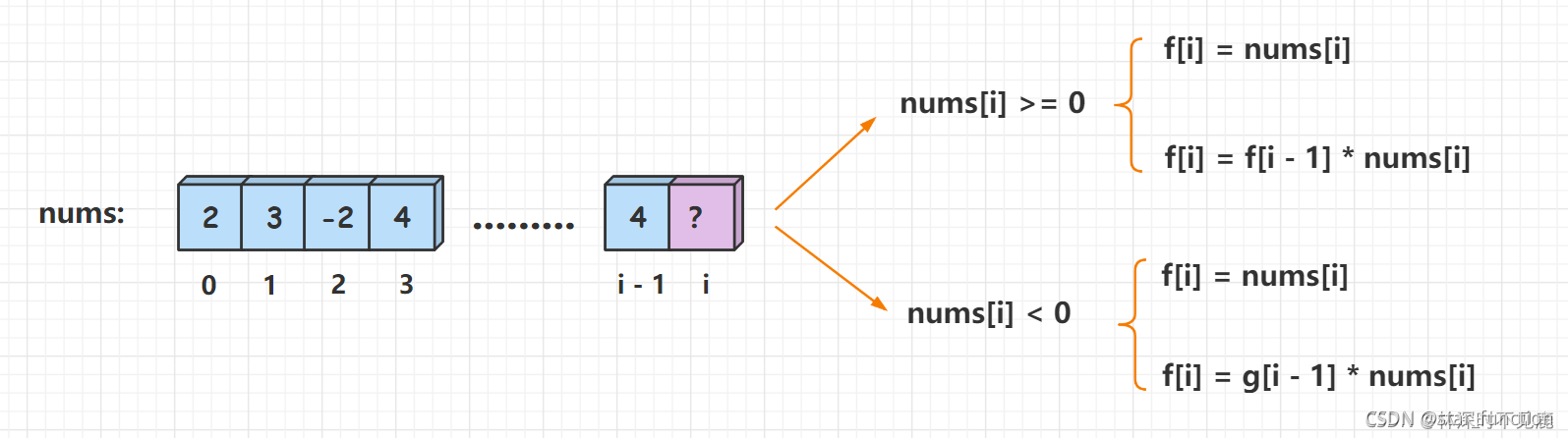
一个正数乘一个正数还是一个正数,一个正数乘一个负数就是一个负数,两个负数相乘是正数。我们无法确定 nums[i] 是正数、负数还是0,因此需要分情况讨论。
当 nums[i] 为正数时,以 nums[i - 1] 结尾的最大子数组的乘积越大越好。
当 nums[i] 为负数时,以 nums[i - 1] 结尾的最大子数组的乘积越小越好。
(例如:-1 > -9,负的绝对值越大数越小)
当 nums[i] 为 0 时,数组乘积都为 0 。
综上所述,我们不仅需要计算以 nums[i] 结尾的子数组的乘积的最大值,还需计算以 nums[i] 结尾的子数组的乘积的最小值。记最大值数组的初始值为 maxdp[0],最小值数组的初始值为 mindp[0]。
基础条件 maxdp[0] = nums[0]; mindp[0] = nums[0];
状态转移方程
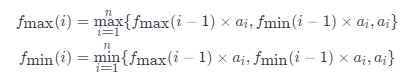
第 i 个元素结尾的乘积最大子数组的乘积为:第 i - 1 个元素结尾的乘积最大子数组的乘积与当前元素的乘积 和 第 i - 1 个元素结尾的乘积最小子数组的乘积与当前元素的乘积 还有 当前元素,三者间的最大值。
C++代码表示如下
maxdp[i] = max(max(maxdp[i - 1] * nums[i], nums[i]), mindp[i - 1] * nums[i]);
mindp[i] = min(min(mindp[i - 1] * nums[i], nums[i]), maxdp[i - 1] * nums[i]);
这里有个问题,为啥要和元素自身比大小?
因为乘积可能是负值,那么元素自身要是正值,二者之积还不如元素本身大。
因此考虑使用元素本身,从当前元素重新开始。
2.3 返回最值
经过状态转移后,我们得到了最大值数组。题目要求返回最大值,因此需要遍历数组,找到最大值并返回。
具体代码如下:
class Solution {
public:
int maxProduct(vector<int>& nums) {
vector<int> maxdp(nums);
vector<int> mindp(nums);
if(nums.size() == 0) return 0;
if(nums.size() == 1) return nums[0];
// maxdp[0] = nums[0]; mindp[0] = nums[0];
for(int i = 1; i < nums.size(); i++)
{
maxdp[i] = max(max(maxdp[i - 1] * nums[i], nums[i]), mindp[i - 1] * nums[i]);
mindp[i] = min(min(mindp[i - 1] * nums[i], nums[i]), maxdp[i - 1] * nums[i]);
}
int result = maxdp[0];
for(int j = 1; j < maxdp.size(); j++)
{
result = result < maxdp[j] ? maxdp[j] : result;
}
return result;
}
};
2.4 报错解决
使用 vector 数组时,一定要注意先分配空间,在索引访问,否则就会报 runtime error: reference binding to null pointer of type ‘int‘ (stl_vector.h) 的错误。
如 vector<int> maxdp(nums);不可以写成 vector<int> maxdp;
否则使用 maxdp[i] = max(max(maxdp[i - 1] * nums[i], nums[i]), mindp[i - 1] * nums[i]); 类似的语句就会报错
3. 空间优化
第 i 个状态只与第 i - 1个状态相关,因此可以使用两个变量代替两个数组来存储结果。maxdp 代表最大值,mindp 代表最小值。
需要注意的是,最大值和最小值要做到同时更新,因此用临时变量 tmp 来存储最大值,每次遍历比较之前的最大值和当前最大值,返回较大的那个。
具体代码如下
class Solution {
public:
int maxProduct(vector<int>& nums) {
if(nums.size() == 0) return 0;
if(nums.size() == 1) return nums[0];
int result = nums[0];
int maxdp = nums[0]; int mindp = nums[0];
for(int i = 1; i < nums.size(); i++)
{
int tmp = maxdp;
maxdp = max(max(nums[i] * maxdp, nums[i]), nums[i] * mindp);
mindp = min(min(mindp * nums[i], nums[i]) , nums[i] * tmp);
result = max(result, maxdp);
}
return result;
}
};