[数据结构与算法]CCF-CSP-202109-2：非零段划分（题解）

问题描述

• 题目来源：CCF-CSP-202109-2：非零段划分

解题思路

非零段数量的计算

????在数组$A$的开头和结尾处各加一个$0$，可以清楚地看出：每一个非零段数量的结尾都与0紧邻。

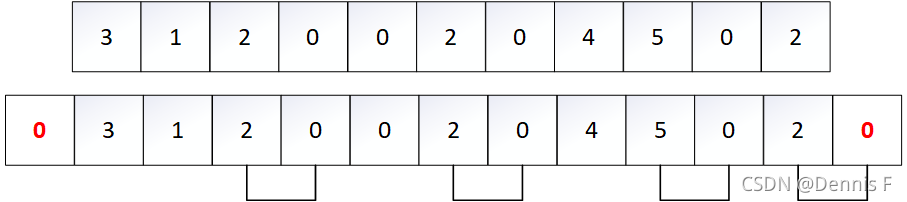
非零段数量的更新

????正整数$p$的取值范围为$A_1+1,A_2+1,\dots \dots A_n+1$去重后的集合。$p$取其他值的效果最终会与取上述值的效果一致。
????我们将$A_1+1,A_2+1,\dots \dots A_n+1$排序、去重后的结果记作：
$$1\le a_1+1<a_2+1<\dots \dots <a_k+1,a_i(1\le i\le k)\in A$$
????同时，$p$取$a_i+1(1\le i\le k)$得到的非零段数量$PeriodNu{m}_i$可以在$p$取$a_{i?1}+1$得到的非零段数量$PeriodNu{m}_{i?1}$上得到，这样可以避免重复计算。
????我们只需要在$p$取$a_{i?1}+1$得到的数组A的基础上，将$a_i$依次替换为$0$。并根据以下规则（以$a_i=1$为例）由$PeriodNu{m}_{i?1}$得到$PeriodNu{m}_i$：

AC代码

#include <iostream>
#include <vector>
#include <set>
#include <map>

using namespace std;

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    int n;
    cin >> n;

    vector<int> A;
    set<int> DiffNumList;         // 用set将A中的数字去重、排序
    map<int, vector<int>> NumPos; // NumPos将不同数字的位置分别记录下来

    A.push_back(0); //在A开头添加一个0
    for (int i = 1; i <= n; ++i)
    {
        int Num;
        cin >> Num;

        A.push_back(Num);
        DiffNumList.insert(Num);
        NumPos[Num].push_back(i);
    }

    int PeriodNum = 0;

    A.push_back(0); //在A结尾添加一个0
    for (int i = 1; i <= n; ++i)
    {
        if (A[i] != 0 && A[i + 1] == 0)
        {
            ++PeriodNum;
        }
    }

    int maxPeriodNum = PeriodNum;
    for (int Num : DiffNumList)
    {
        if (Num == 0)
            continue;

        for (int i = 0; i < NumPos[Num].size(); ++i)
        {
            int beginIndex = NumPos[Num][i], endIndex = beginIndex;

            if (A[beginIndex] == 0)
                continue; // 在之前的循环中已经将连着的Num变为了0

            while (A[endIndex] == Num) // 找到相邻的Num
            {
                A[endIndex] = 0;
                ++endIndex;
            }
            endIndex -= 1;

            if (A[beginIndex - 1] == 0 && A[endIndex + 1] == 0)
                --PeriodNum; // 少一个非零段
            else if (A[beginIndex - 1] != 0 && A[endIndex + 1] != 0)
                ++PeriodNum; // 多一个非零段
        }

        maxPeriodNum = max(PeriodNum, maxPeriodNum);
    }

    cout << maxPeriodNum << endl;

    return 0;
}