编程任务
编写一个程序,任意给定一个正实数,计算该实数的近似平方根。
编程要点
1、理解牛顿迭代法;
2、掌握使用牛顿迭代法计算任意正实数近似平方根的算法。
算法思路
可以设任意正实数为a,a的平方根为x,列出等式:
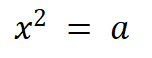
变换为方程 V:
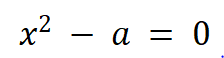
这个等式是一元二次方程,解方程即可求得x。现在正实数平方根计算问题已转换为解一元二次方程问题。
牛顿迭代法
先前掌握的解一元二次方程的公式用到了开方,即平方根计算,因此在计算平方根时,不能使用解一元二次方程的公式。
解方程公式虽然不能使用,但我们可以使用牛顿迭代法来找到方程的近似根,牛顿迭代法的主要思想是逼近和迭代。
牛顿迭代法也称牛顿-拉弗森方法,该方法主要是通过逼近和迭代寻找无解方程的近似根。下面给出求方程 V 的具体步骤。
(1)方程V变量x赋初值x0,作为方程的近似根;
(2)迭代过程:
? ? ? ? ? ?①?? 计算方程V的下一个近似根x1;
????????????计算公式:
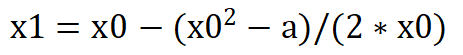
????????????其中,2*x0是方程V的导函数
????????????②?计算x0和x1差的绝对值differ;
? ? ? ? ? ? ③? ?若differ小于指定的数值,则认为x1为方程V的近似根,执行第④个步骤,否则继续执行迭代;
? ? ? ? ? ? ④ 返回x1,迭代结束。
计算正实数平方根 Python代码?
import math
# 计算实数平方根的方程
def f1(x,a):
return x*x-a
# 计算实数平方根方程的导函数
def f2(x):
return 2*x
# 计算实数的平方根
def sqrt(a):
# x0为方程的初始值,作为方程的初始近似根
x0 = a/2
# 计算方程的下一个近似根x1
x1 = x0 - f1(x0,a)/f2(x0);
# 计算两个近似根x0和x1差的绝对值
differ = math.fabs(x1-x0)
# 循环计算方程的近似根,直至两个近似根差的绝对值小于1e-5
while( differ >= 1e-5 ):
# x0被赋值为x1
x0 = x1
# 计算方程的下一个近似根x1
x1 = x0 - f1(x0,a)/f2(x0);
# 计算两个近似根x0和x1的绝对差
differ = math.fabs(x1-x0)
return x1
# 程序入口
if __name__ == '__main__':
a = input("请输入一个正实数:\n")
print("%.5f" % sqrt(float(a)))
理解牛顿迭代法
要理解牛顿迭代法,需要先理解曲线的切线是曲线的线性逼近,线性逼近就是用曲线某点的切线来近似该点附近的曲线。
下面通过绘图来理解牛顿迭代法,绘制图形可以使用Python语言,也可以使用matlab语言。
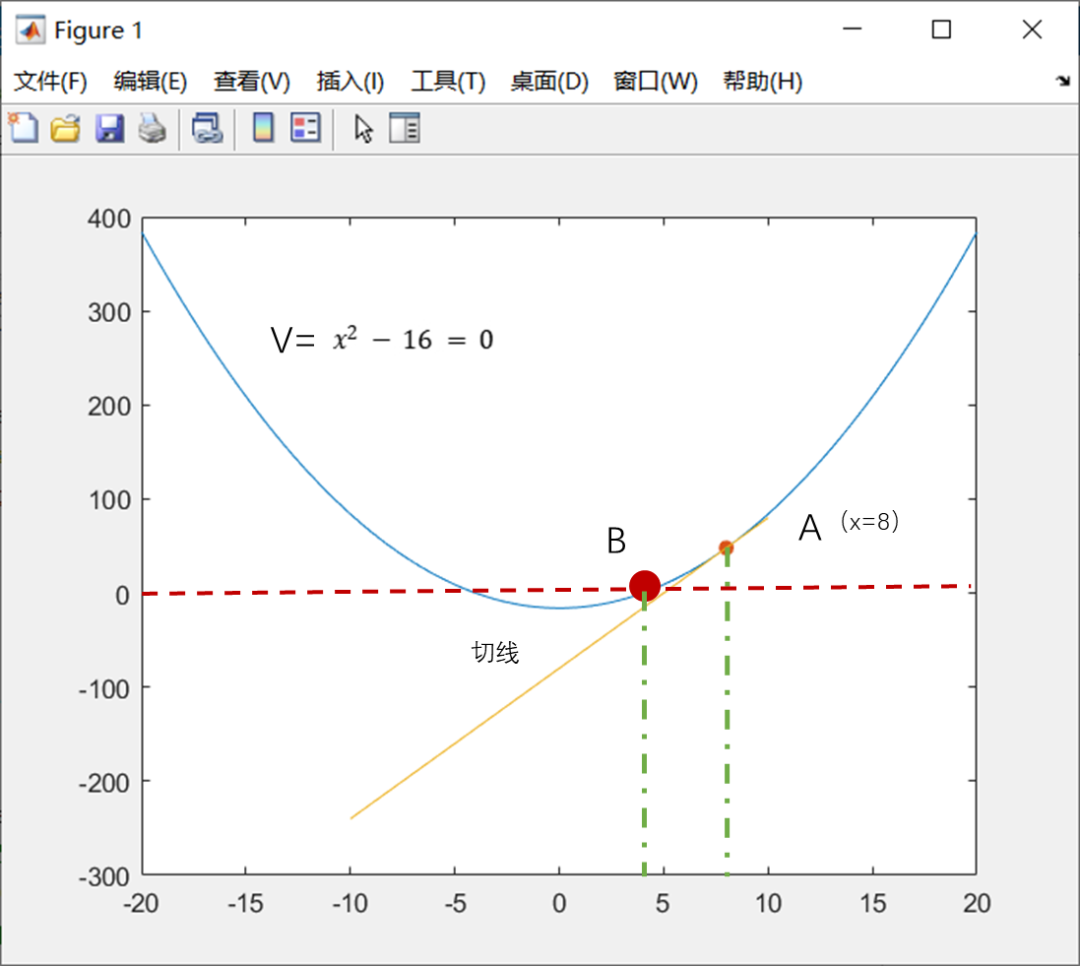
图 1-1 曲线的切线
图1-1绘制了方程V的曲线和曲线上A点的切线,观察图1-1可知,切线在曲线的A点处非常靠近曲线,在A点处,当方程变量x取得很小变化dx时,曲线和切线几乎很难区分。因此可以说在曲线A点处的切线是方程V的线性逼近。
图1-1中红色直线与曲线的交点B点是方程V的正根,A点距离B点还有一段距离,我们希望A点继续沿曲线移动到B点,B点就是方程的解。
如何移动A点呢?这就用到了切线方程,A点的切线方程为(n=8):
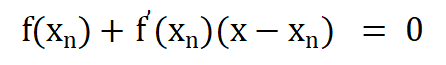
由A点的切线方程推出:
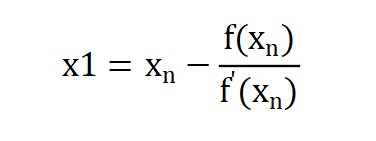
x1是过A点切线方程与X轴交点的横坐标,过点(x1,f(x1))继续做方程V的切线,由过点(x1,f(x1))的切线方程计算得到x2。依次类推,直至A点移动到B点或x1与x2差的绝对值小于指定的一个非常小的数,整个迭代结束。
注意要点
使用牛顿迭代法要找到方程的近似根,必要条件是函数在定义域内是连续的,且存在二阶导数。初始值的选择也很重要,若初始值选择的不合适,会导致找不到近似根。
不过求解实数平方根问题,使用牛顿迭代法是安全的。
附加matlab绘图代码
% 在区间[-1,1]内创建100个x坐标数据点
x = linspace(-20,20,100);
% 计算f(x)=x^2函数的y坐标
y = x.^2-16;
% 绘制曲线
plot(x,y)
hold on
% 绘制曲线点(x=8)的切线
draw_line(8,8*8-16)
% 定义绘制切线函数
function draw_line(x,y)
% 绘制数据点
scatter(x,y,'filled')
% 计算函数y=x^2曲线(x,y)点的切线斜率
k = 2 * x
x1 = linspace(-10,10,100)
% 通过切线方程计算y数据
y1 = k*(x1-x)+y
% 绘制切线
plot(x1,y1)
end
?