[数据结构与算法]算法学习-广度优先搜索

概念介绍

本博客在学习北京大学陈斌老师《数据结构与算法》MOOC课程中总结反思形成。

词梯问题的要求：

从一个单词演变到另一个单词，其中的过程可以经过多个中间单词，要求相邻两个单词之间差异只能是1个字母， 如FOOL变SAGE：

FOOL >> POOL >> POLL >> POLE >> PALE >>SALE >> SAGE

词梯问题的解决步骤：

1. 将可能的单词之间的演变关系表达为图；
2. 采用“广度优先搜索 BFS”，来搜寻从开始单词到结束单词之间的所有有效路径；
3. 选择其中最快到达目标单词的路径；

广度优先搜索算法：

• 给定图G，以及开始搜索的起始顶点s
• BFS搜索所有从s可到达顶点的边
• 而且在达到更远的距离k+1的顶点之前，BFS会找到全部距离为k的顶点
• 可以想象为以s为根，构建一棵树的过程，从顶部向下逐步增加层次
• 广度优先搜索能保证在增加层次之前，添加了所有兄弟节点到树中

个人理解：广度优先搜索算法，直观理解就是按行平移换行

代码解析

建立单词关系图

4字母单词表下载资源链接：https://download.csdn.net/download/qq_43337291/29213425

代码分析：

样例数据文件一共3903个单词，建立了7473个桶（最多建立$3903\times 4=15612$个桶 ）
邻接矩阵：3903*3903 = 15233409矩阵单元
单词关系图：42004边

稀释度：$\frac{42004}{15233409}=0.27$

from pythonds.graphs.adjGraph import Graph
from pythonds.basic.queue import Queue

def buildGraph(wordFile):
    d = {}
    g = Graph()
    wfile = open(wordFile, 'r')
    # 创建桶（只有一个字母不同）4字母单词可以属于四个桶
    for line in wfile:
        word = line[:-1]
        for i in range(len(word)):
            bucket = word[:i] + '_' + word[i + 1:]
            if bucket in d:
                d[bucket].append(word)
            else:
                d[bucket] = [word]

    # 同一个桶单词之间建立边
    _count = 0
    for bucket in d.keys():
        for word1 in d[bucket]:
            for word2 in d[bucket]:
                if word1 != word2:
                    g.addEdge(word1, word2)
                    _count += 1
    print("num of edges:{}".format(_count))
    return g

广度优先搜索算法

顶底具备的辅助属性：

• 距离distance：从起始顶点到此顶点路径长度；
• 前驱顶点predecessor：可反向追溯到起点；
• 颜色color：标识了此顶点是尚未发现（白色）、已经发现（灰色）、还是已经完成探索（黑色）

队列作用：

用一个队列Queue来对已发现的顶点进行排列决定下一个要探索的顶点（队首顶点）

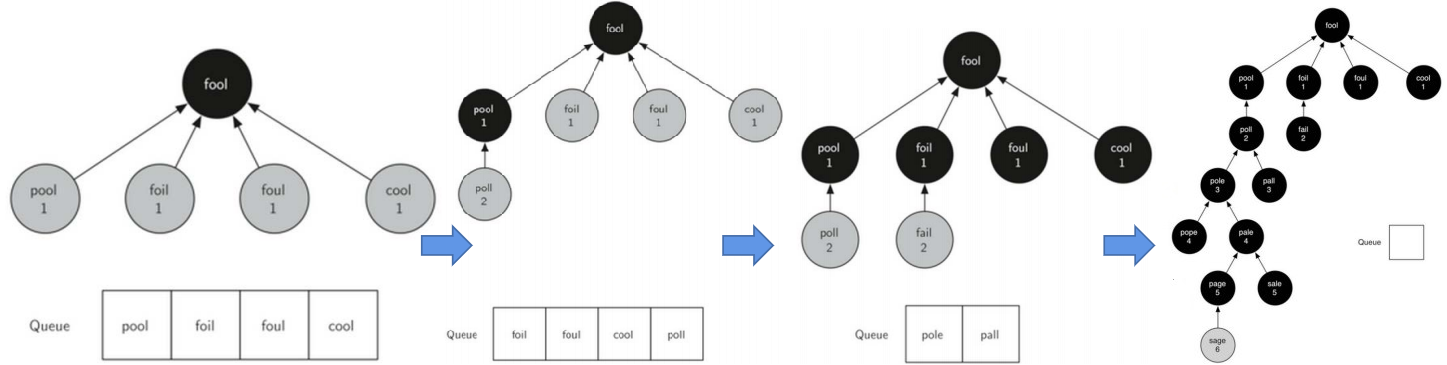
代码分析：

# BFS算法代码 Breadth First Search
def bfs(g, start):
    start.setDistance(0)
    start.setPred(None)
    vertQueue = Queue()
    vertQueue.enqueue(start)
    while (vertQueue.size() > 0):
        # 取队首作为当前顶点
        currentVert = vertQueue.dequeue()
        # 遍历邻接顶点
        for nbr in currentVert.getConnections():
            if (nbr.getColor() == 'white'):
                nbr.setColor('gray')
                nbr.setDistance(currentVert.getDistance() + 1)
                nbr.setPred(currentVert)
                vertQueue.enqueue(nbr)
        # 当前顶点设为黑色
        currentVert.setColor('black')

回途追溯函数

在以FOOL为起始顶点，遍历了所有顶点，并为每个顶点着色、赋距离和前驱之后，即可以通过一个回途追溯函数来确定
FOOL到任何单词顶点的最短词梯。

BFS算法复杂度分析

• while循环对每个顶点访问一次，所以是$O(|V|)$；

• 嵌套在while中的for，由于每条边只有在其起始顶点u出队的时候才会被检查一次，而且每个顶点最多出队1次，所以边最多被检查1次，一共是$O(|E|)$;

• 综合起来BFS的时间复杂度为$O(|V|+|E|)$。