并查集能解决连通性问题,如 A = B , B = C , C = D A = B,B=C,C=D A=B,B=C,C=D 能推导出 A = D A=D A=D。
1. 连通性问题
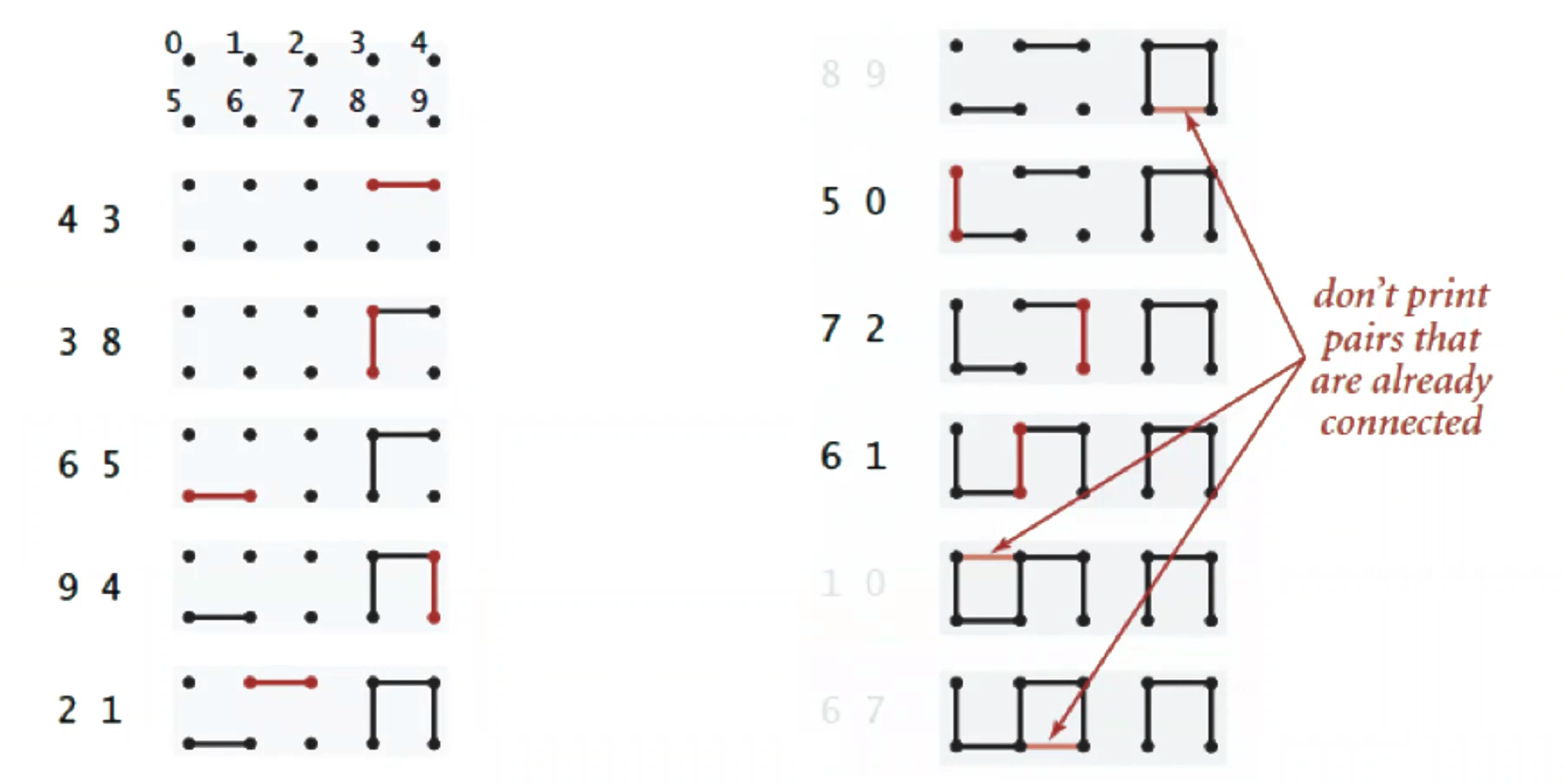
- 基于 染色 的思想,一开始所有点的颜色不同
- 连接两个点的操作,可以看成将 一种颜色 的点染成 另一种颜色
- 如果两个点颜色 一样,证明连通,否则不连通
- 这种方法叫做并查集的【Quick-Find算法】
2. Quick-find
2.1 讲解
开辟一个数组,保存 0~9 的值,一开始颜色都不同,即将该数组里的每个位置的数初始化为该值。

next: [4 -- 3] 表示将 4 和 3 建立联系,就将数组中 4 号位置的值修改为3,表示将 4 号点染成 3 号点的颜色:

将 4 号点和 8 号点建立联系,即将 4 号点染成 8 号点的颜色,遍历每个点看是否和 4 号点的颜色相同,如果相同则都要染成 8 号点的颜色。每次修改颜色都要去遍历所有点,所以 Quick-find 算法中修改点颜色的时间复杂度为
O
(
n
)
O(n)
O(n),而判断连通关系的时间复杂度为
O
(
1
)
O(1)
O(1),即判断数组中保存的值是否相同:
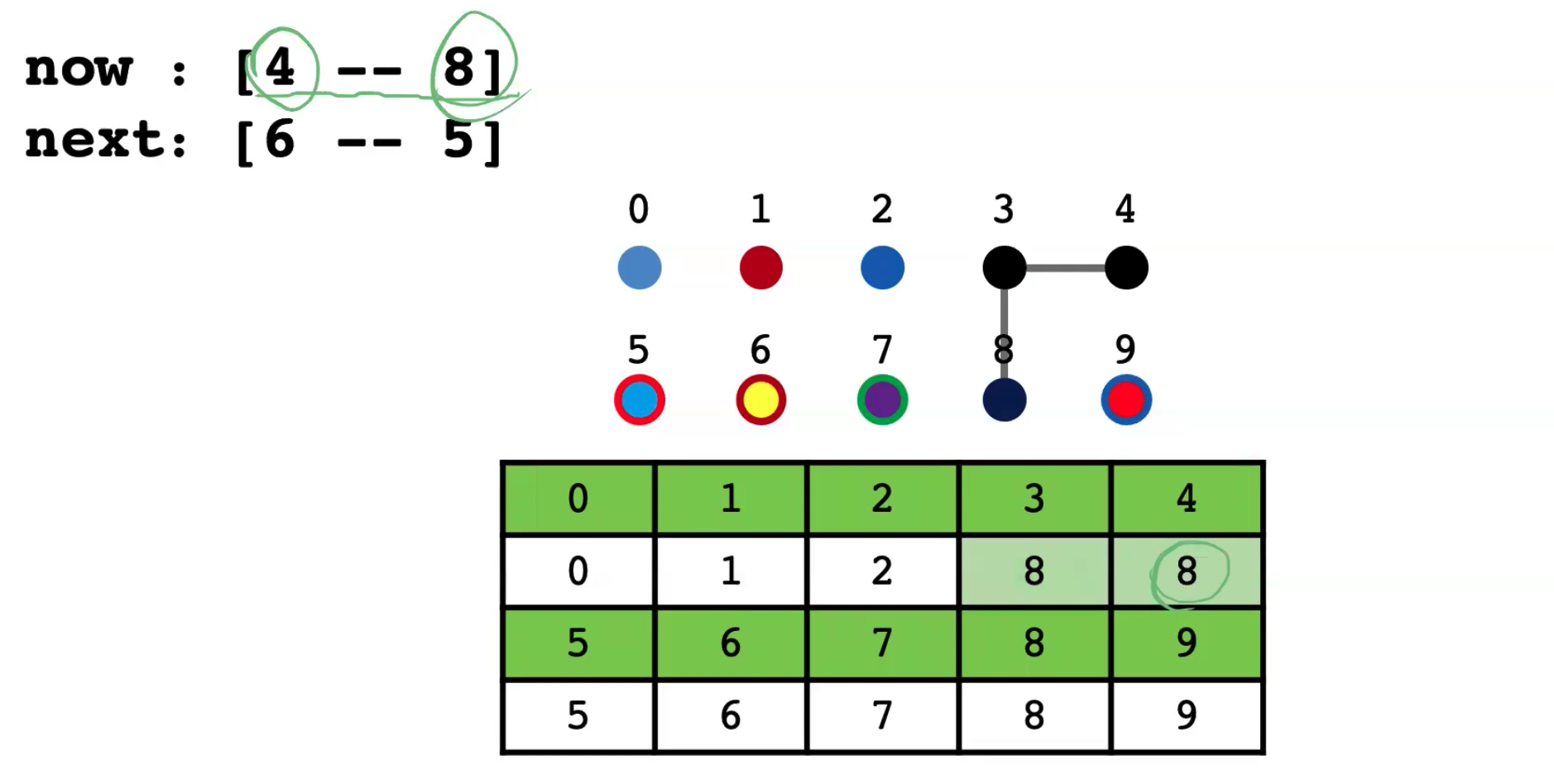
连通 6 和 5:

连通 9 和 4:

连通 2 和 1:

连通 5 和 0:

连通 7 和 2:

连通 6 和 1:

最终可以发现,数组中只有 2 个值,相当于 2 个集合建立了连通关系,第一个都染成了 1 号点的颜色,第二个都染成了 8 号点的颜色。
2.2 代码实现
/*************************************************************************
> File Name: 001.quick_find.c
> Author: Maureen
> Mail: Maureen@qq.com
> Created Time: 一 10/ 4 18:23:14 2021
************************************************************************/
#include <stdio.h>
#include <stdlib.h>
typedef struct UnionSet {
int *color;
int n;//并查集空间大小
} UnionSet;
/*
* 并查集的初始化
*/
UnionSet *init(int n) {
UnionSet *u = (UnionSet *)malloc(sizeof(UnionSet));
u->color = (int *)malloc(sizeof(int) * (n + 1)); //将0号位空出
u->n = n;
for (int i = 1; i <= n; i++) {
u->color[i] = i;
}
return u;
}
/*
* 查找,获取x的颜色
*/
int find(UnionSet *u, int x) {
return u->color[x];
}
/*
* 合并a和b点
*/
int merge(UnionSet *u, int a, int b) {
//判断a和b是否连通,利用a和b的颜色来判断
if (find(u, a) == find(u, b)) return 0; //a和b本身就是连通的
int color_a = u->color[a];
for (int i = 1; i <= u->n; i++) { //找到和a颜色相同的点,都染成b点的颜色
if (u->color[i] - color_a) continue;
u->color[i] = u->color[b];
}
return 1;
}
/*
* 并查集的销毁
*/
void clear(UnionSet *u) {
if (u == NULL) return ;
free(u->color);
free(u);
return ;
}
int main() {
int n, m;
scanf("%d%d", &n, &m);
UnionSet *u = init(n);
for (int i = 0; i < m; i++) {
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
switch (a) {
case 1: merge(u, b, c); break;
case 2: printf("%s\n", find(u, b) == find(u, c) ? "Yes" : "No"); break;
}
}
clear(u);
return 0;
}
代码的正确性可以使用 #71. 练习题1:朋友圈 进行验证。
2.3 总结
- 连通判断: O ( 1 ) O(1) O(1)
- 合并操作: O ( n ) O(n) O(n)
问题思考:
quick-find算法的连通判断非常快,可是合并操作非常慢- 本质上问题中只是需要知道一个点与哪些点的颜色相同
- 而若干点的颜色可以通过间接指向同一个节点
- 合并操作时,实际上是将一棵树作为另一个棵树的子树
3. Quick-union
3.1 讲解
视频讲解
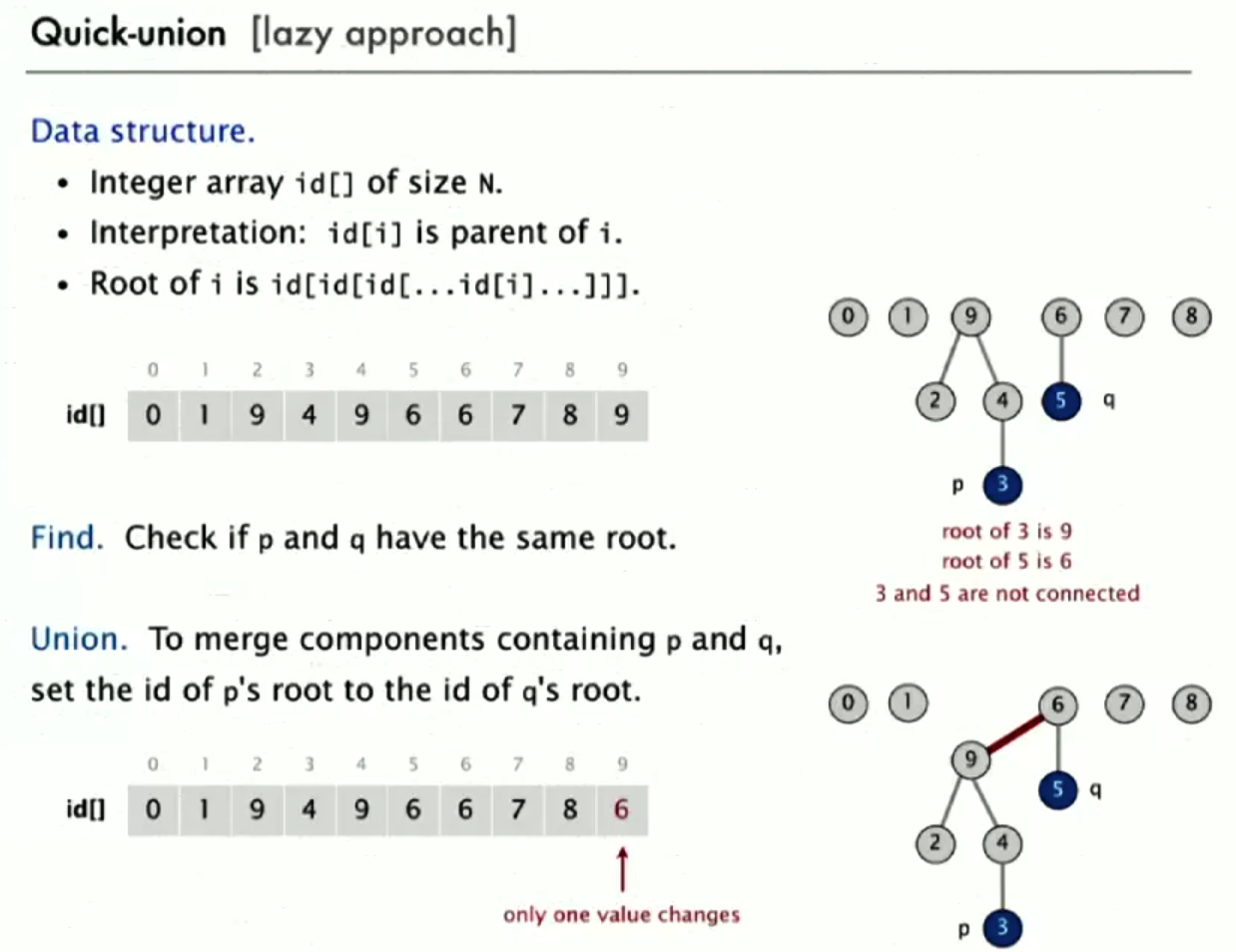
id 数组的意义是 i 的根是 id[i]
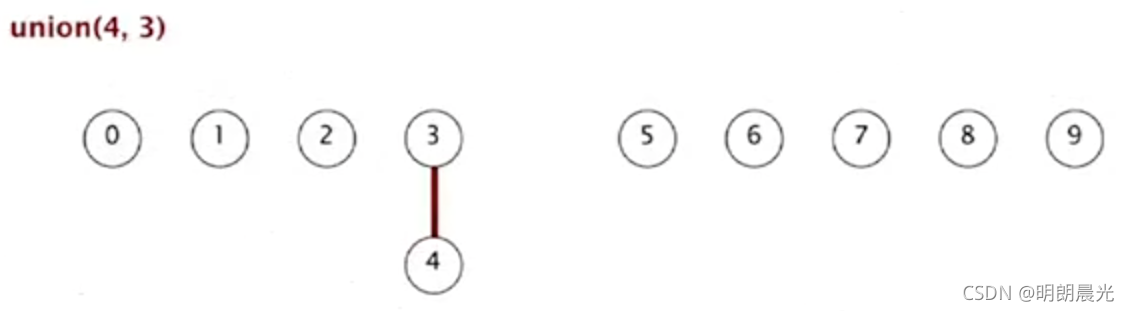
合并过程:
- 初始:每个点都是自己的根

- union(4,3):4 的父亲变为 3
- union(3,8):3 的父亲是 8

- union(6,5): 6 的父亲是 5
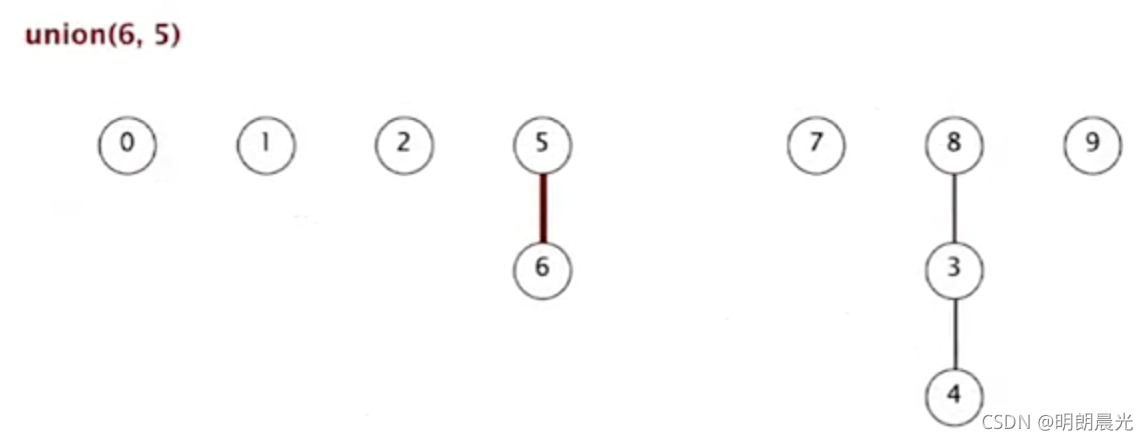
- union(9,4):4 的根为 8,所以 9 的父亲为 8
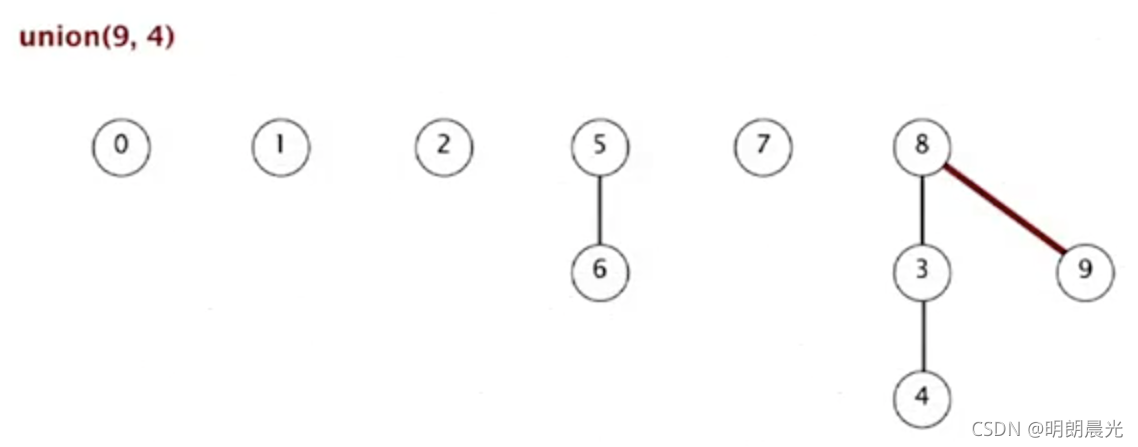
- union(2,1):2 的父亲为 1
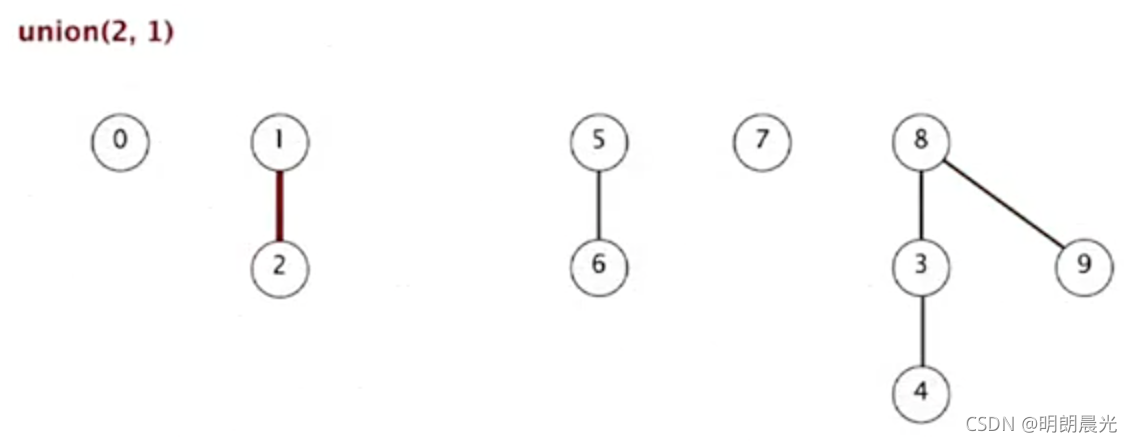
- connected(8,9):8 和 9 的根相同,所以 8 和 9 是连通的

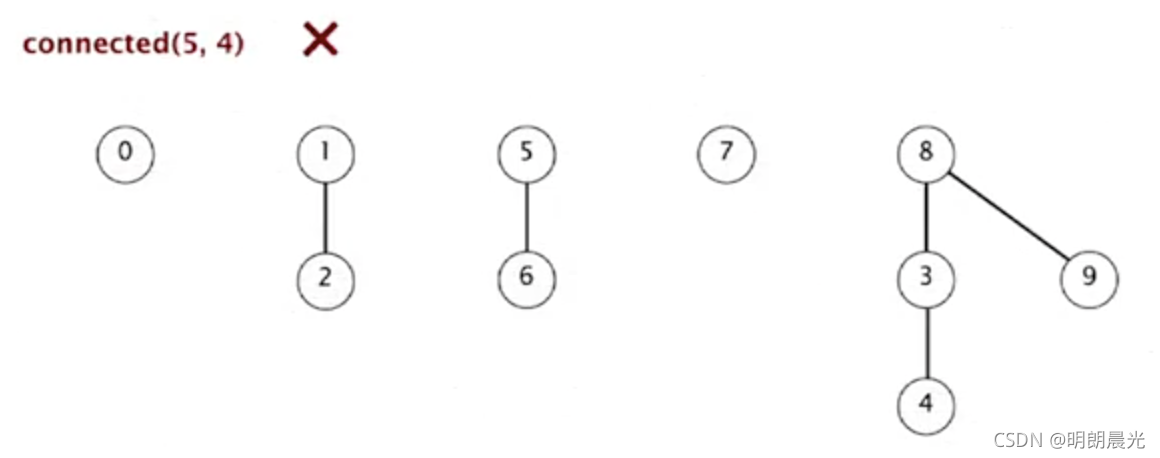
- connected(5,4):5 的根为 5, 4 的根为8,二者不同,所以不连通
- union(5,0):5 的父亲是 0

- union(7,2):2 的根为 1, 所以 7 的父亲是 1
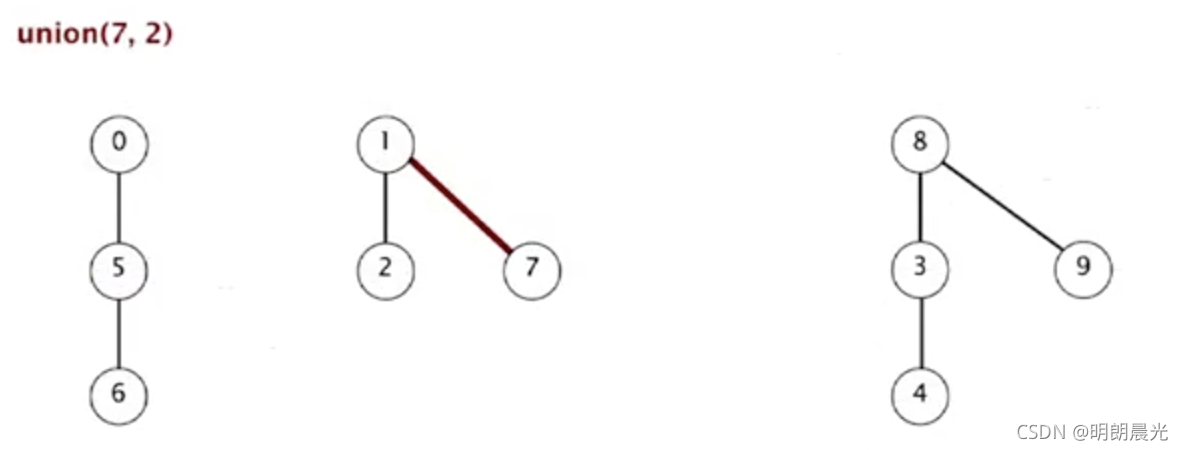
- union(6,1):6 的根为0, 1 的根为1, 所以 0 是 1 的孩子

这些 Union 操作中的每一个操作只会更改数组中的一个数据。 - union(7,3): 7 的根为1, 3 的根为 8,所以 1 的父亲是 8
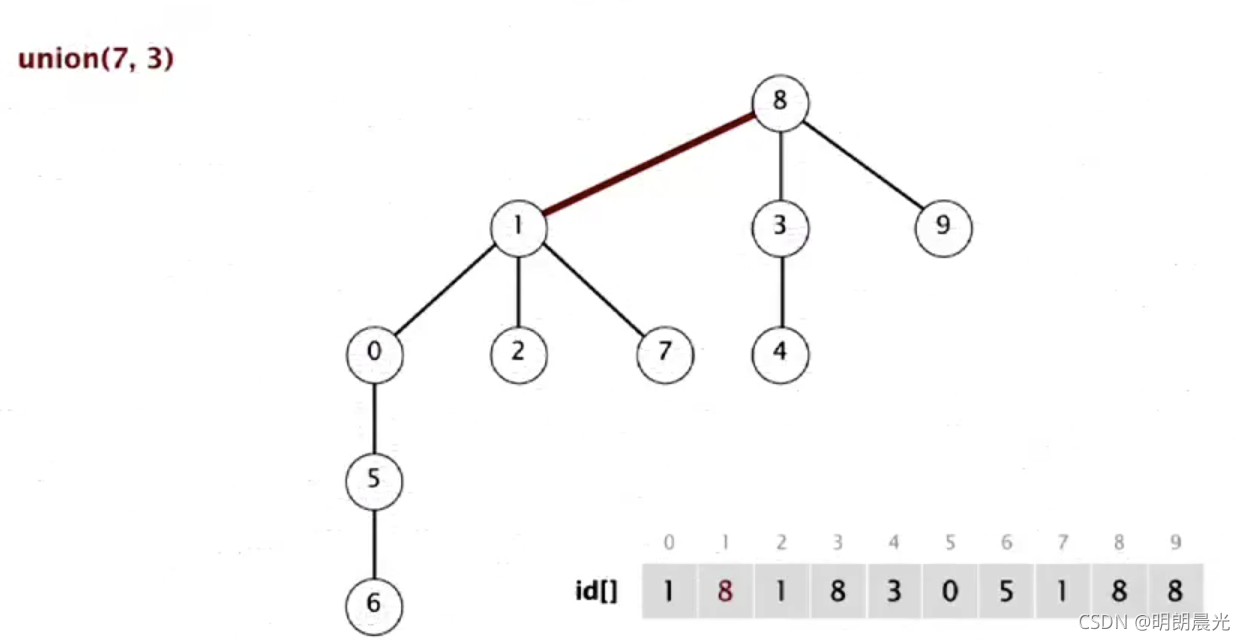
- 最终的结果:·

3.2 代码实现
视频讲解中的代码实现:
public class QuickUnionUF {
private int[] id;
public QuickUnionUF(int n) {
id = new int[n];
//set id of each object to itself (n array accesses)
for (int i = 0; i < n; i++) id[i] = i;
}
private int root(int i) {
//chase parent pointers until reach root (depth of i array accesses)
while (i != id[i]) i = id[i];
return i;
}
public boolean connected(int p, int q) {
//check if p and q have same root (depth of p ans q array accesses)
return root(p) == root(q);
}
public void union(int p, int q) {
//change root of p to point to root of q (depth of p and q array accesses)
int i = root(p);
int j = root(q);
id[i] = j;
}
}
C语言实现:
/*************************************************************************
> File Name: 002.quick_union.c
> Author: Maureen
> Mail: Maureen@qq.com
> Created Time: 四 10/ 7 00:33:14 2021
************************************************************************/
#include <stdio.h>
#include <stdlib.h>
typedef struct UnionSet {
int *father; //每个节点代表的是其父节点
int n; //并查集的空间
} UnionSet;
UnionSet *init(int n) {
UnionSet *u = (UnionSet *)malloc(sizeof(UnionSet));
u->father = (int *)malloc(sizeof(int) * (n + 1));
u->n = n;
for (int i = 1; i <= n; i++) u->father[i] = i;
return u;
}
int find(UnionSet *u, int x) {
//x的父亲就是自己
if (u->father[x] == x) return x;
//找x的父亲
return find(u, u->father[x]);
}
int merge(UnionSet *u, int a, int b) {
int fa = find(u, a);
int fb = find(u, b);
if (fa == fb) return 0;
u->father[fa] = fb;
return 1;
}
void clear(UnionSet *u) {
if (u == NULL) return ;
free(u->father);
free(u);
return ;
}
int main() {
int n, m;
scanf("%d%d", &n, &m);
UnionSet *u = init(n);
for (int i = 0; i < m; i++) {
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
switch (a) {
case 1 : merge(u, b, c); break;
case 2 : printf("%s\n", find(u, b) == find(u, c) ? "Yes" : "No"); break;
}
}
clear(u);
return 0;
}
同样,正确性可以通过提交 #71. 练习题1:朋友圈 验证。
3.3 总结

- 连通判断:
tree-height树高 - 合并操作:
tree-height树高
问题思考
- 极端情况下回退化成一条链
- 将节点数量多的接到少的树上面,导致了退化
- 将树高深的接到浅的上面,导致了退化
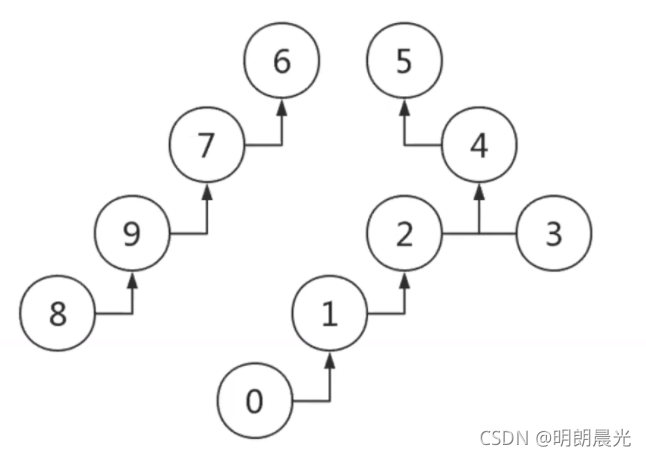
思考:若要改进,是按照节点数量 还是按照 树的高度 为合并参考?
比如判断上图中的8和0是否连通,要向上找根是否相同。
连通判断时间复杂度为 O ( l o g n ) O(logn) O(logn),合并操作的时间复杂度也为 O ( l o g n ) O(logn) O(logn)。
按照节点数量为合并参考更为优秀,因为假设子树 A, S A S_A SA? 表示该树的节点个数;子树B, S B S_B SB? 表示该树节点个数。如果合并前,子树 A 的平均查找次数为 L 1 = ∑ i = 1 S A L i S A L_1 = \frac{\sum_{i=1}^{S_A}L_i}{S_A} L1?=SA?∑i=1SA??Li??,子树B 的平均查找次数为 L 2 = ∑ i = 1 S B L i S B L_2 = \frac{\sum_{i=1}^{S_B}L_i}{S_B} L2?=SB?∑i=1SB??Li?? ,将两棵树合并为一棵树后:
- S A S_A SA? 作为子树,合并后的树的平均查找次数为 L 1 + L 2 + S A S A + S B \frac{L_1+L_2+S_A}{S_A+S_B} SA?+SB?L1?+L2?+SA??
- S B S_B SB? 作为子树,合并后的树的平均查找次数为 L 1 + L 2 + S B S A + S B \frac{L_1+L_2+S_B}{S_A+S_B} SA?+SB?L1?+L2?+SB??
分子加上节点个数,是因为合并后,每个节点的深度都增加了 1。可以发现,平均查找次数和深度无关,而是与节点个数有关,且两种情况的区别在于 S A S_A SA? 和 S B S_B SB? 的差异,所以节点个数少的作为子树,平均查找次数才会少。
于是,基于此,优化为算法weighted quick-union算法,按节点个数进行合并,节点个数少的合并到节点个数多的。
4. Weighted Quick-union
4.1 讲解
先找到根,然后将节点少的树合并到节点多的树下,如果发现结点个数相同,就使用 quick-union 算法将前面一个节点作为子树合并到后面一个节点子树下。
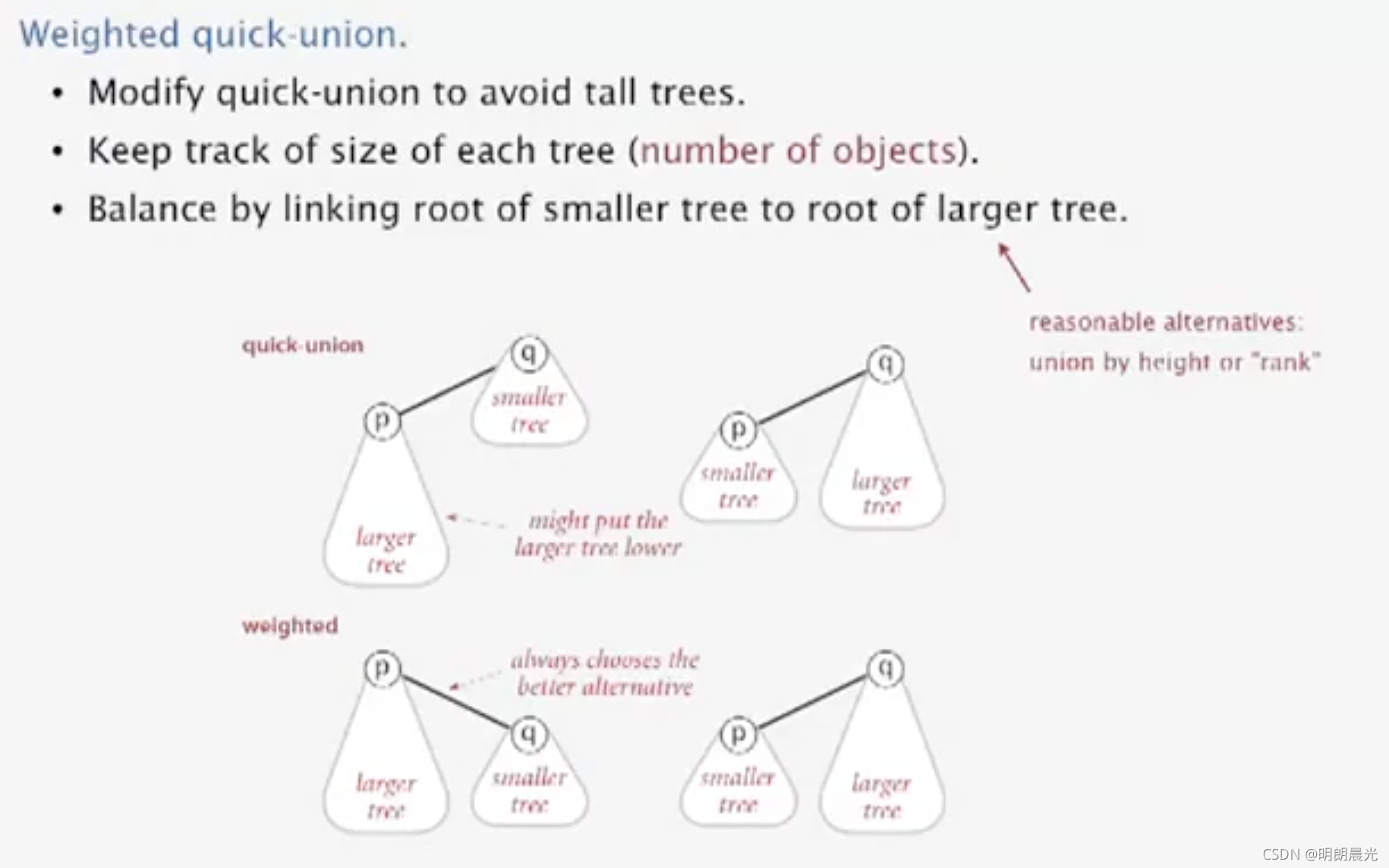
过程演示:
- 起始
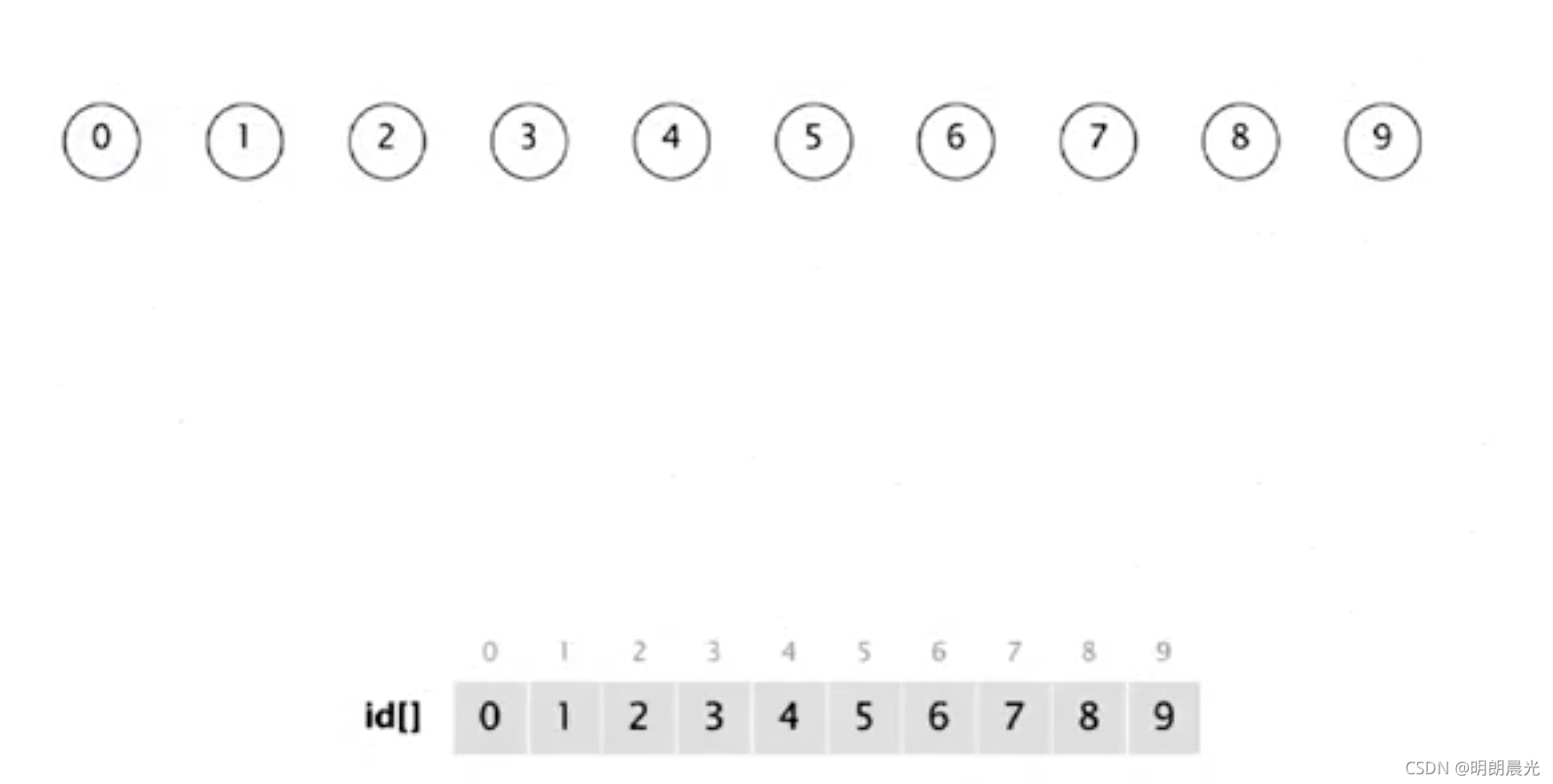
- union(4,3)

- union(3,8):因为 8 是比较小的树
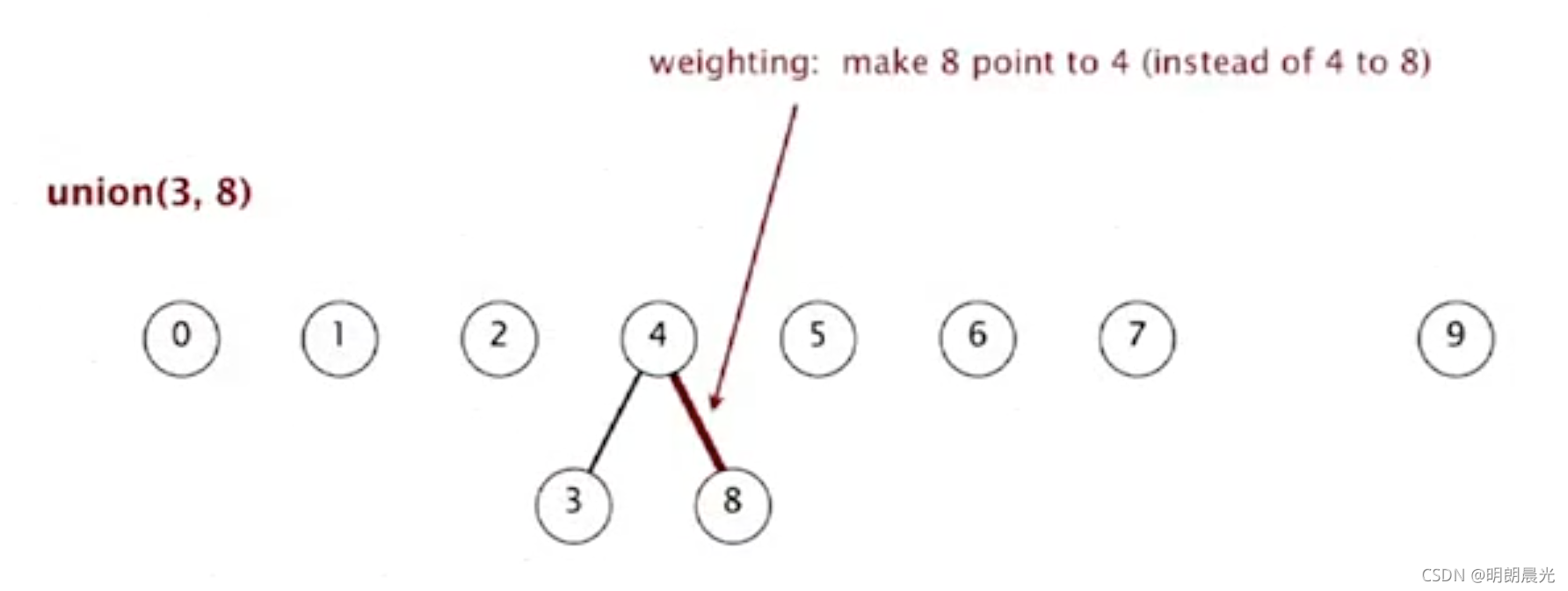
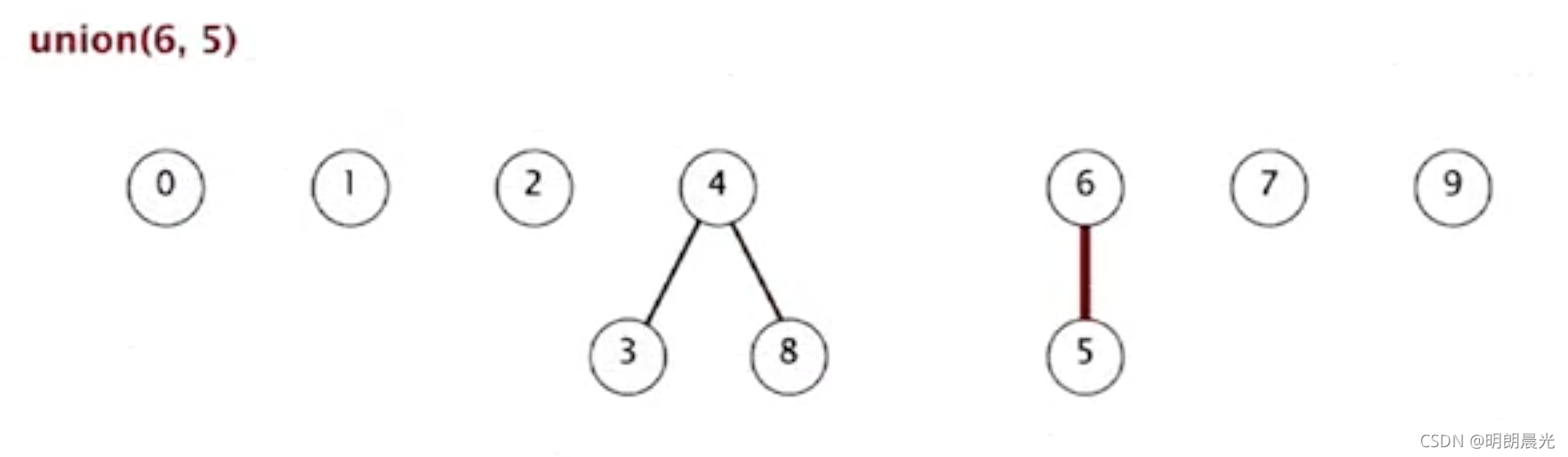
- union(6,5):哪个下降都不重要
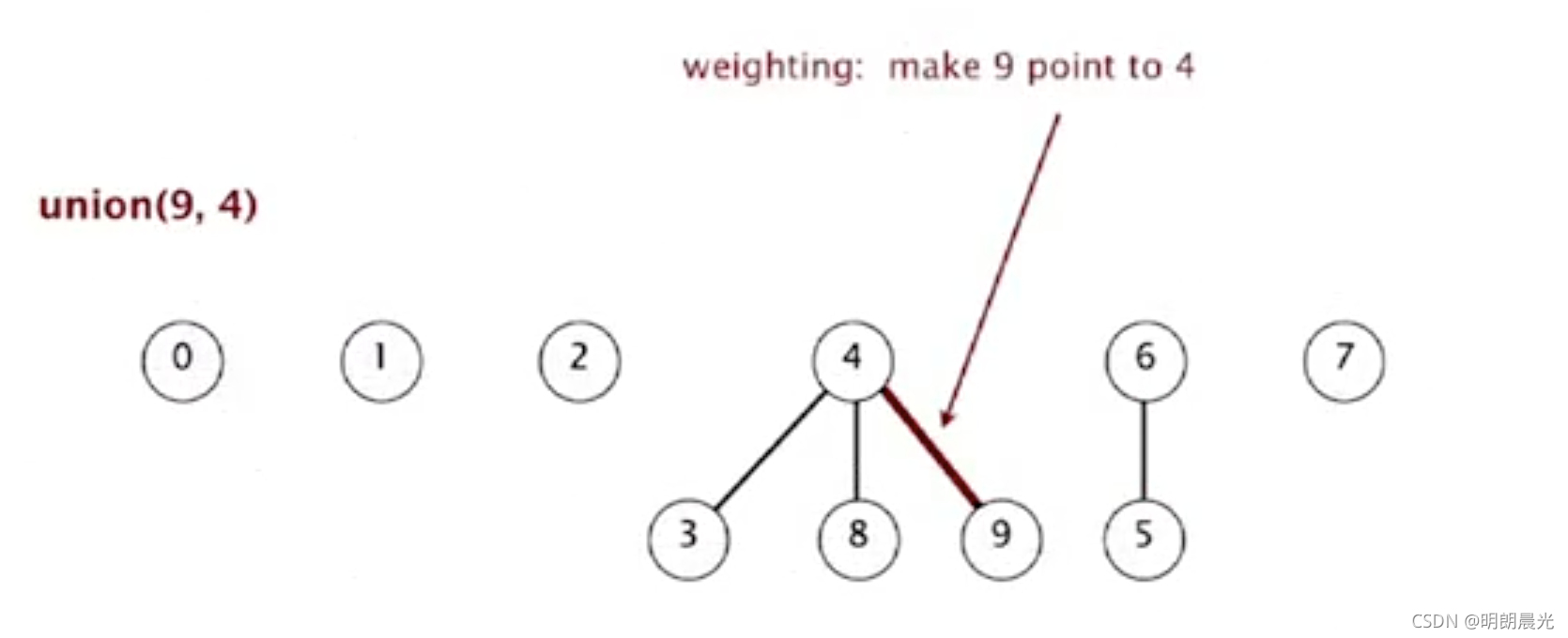
- union(9,4):9 是比较小的树,4是比较大的树
- union(2,1)
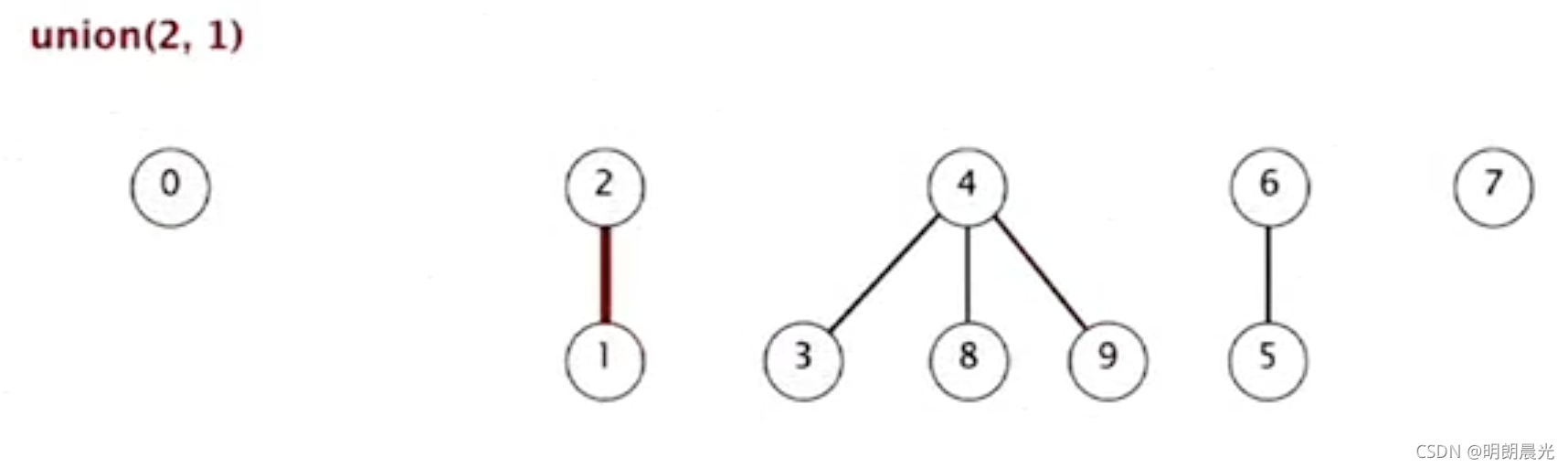
- union(5,0):5所在的树是比较大的树,而0 是小树,所以 0 指向 5 的根 6
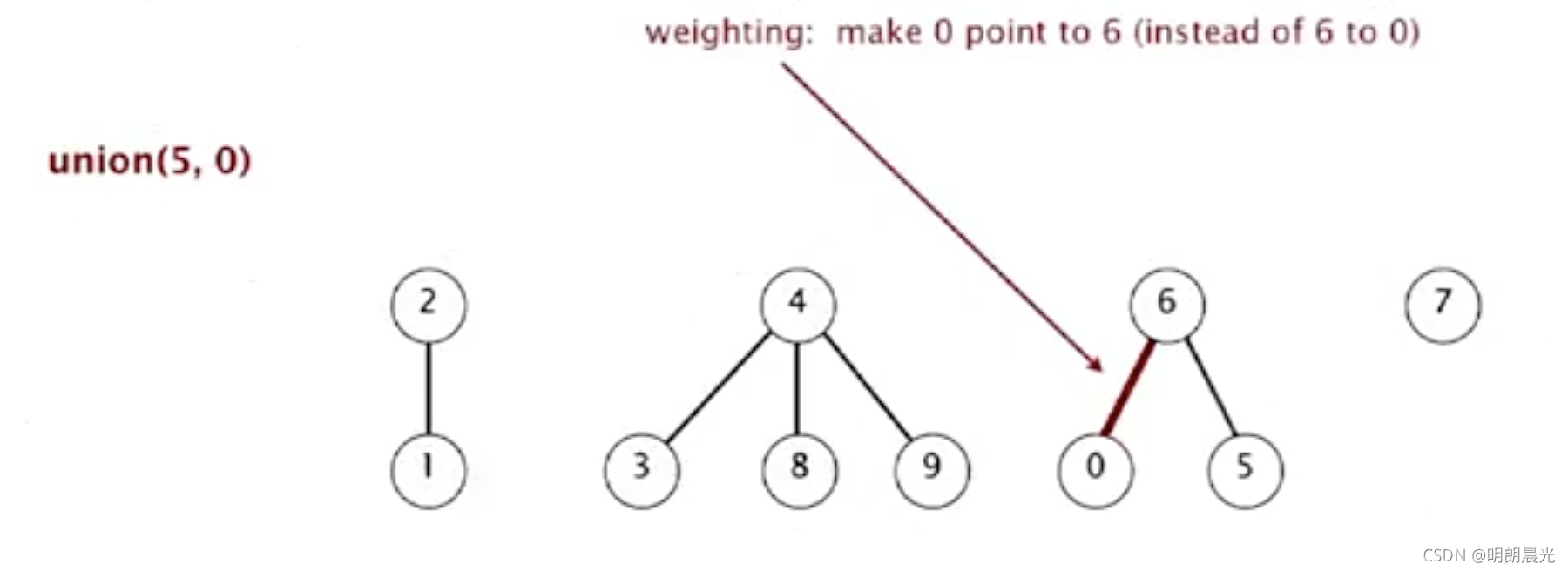
- union(7,2)
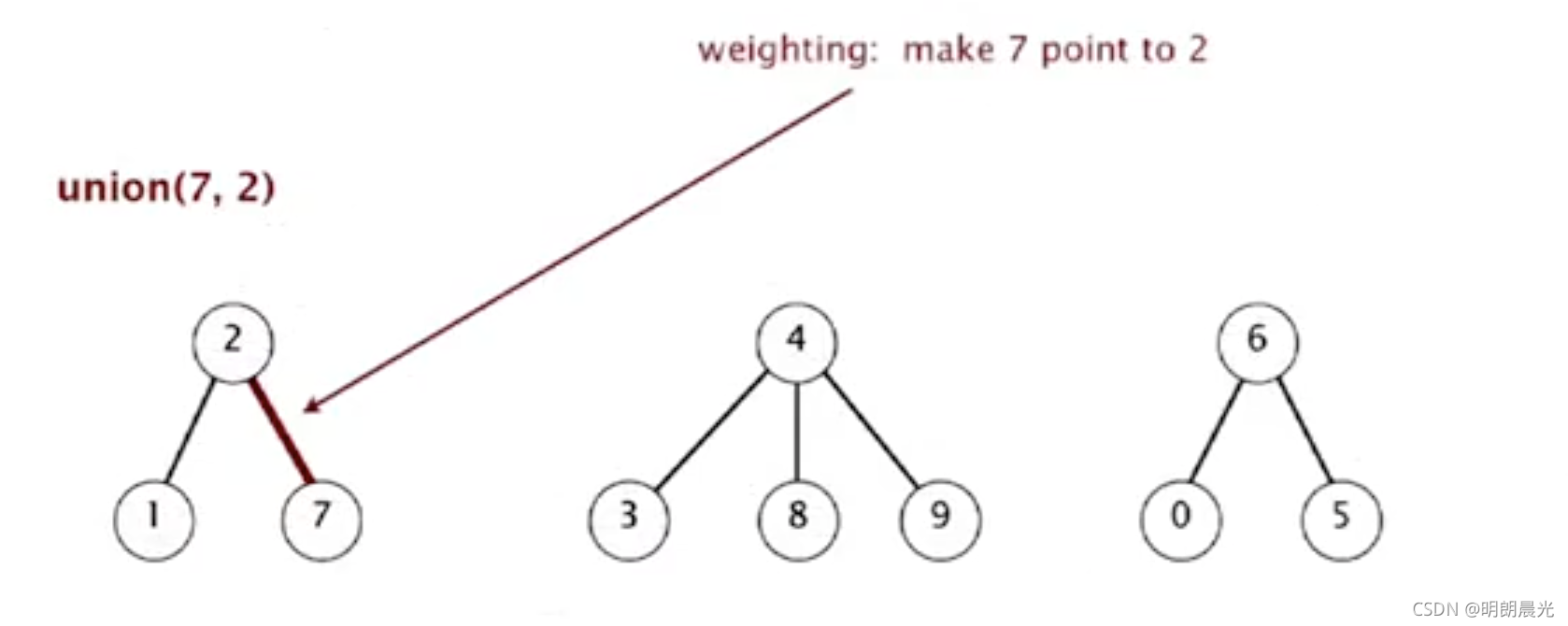
- union(6,1)

- union(7,3)

- 最终结果:

加权算法总是确保较小的树在下面
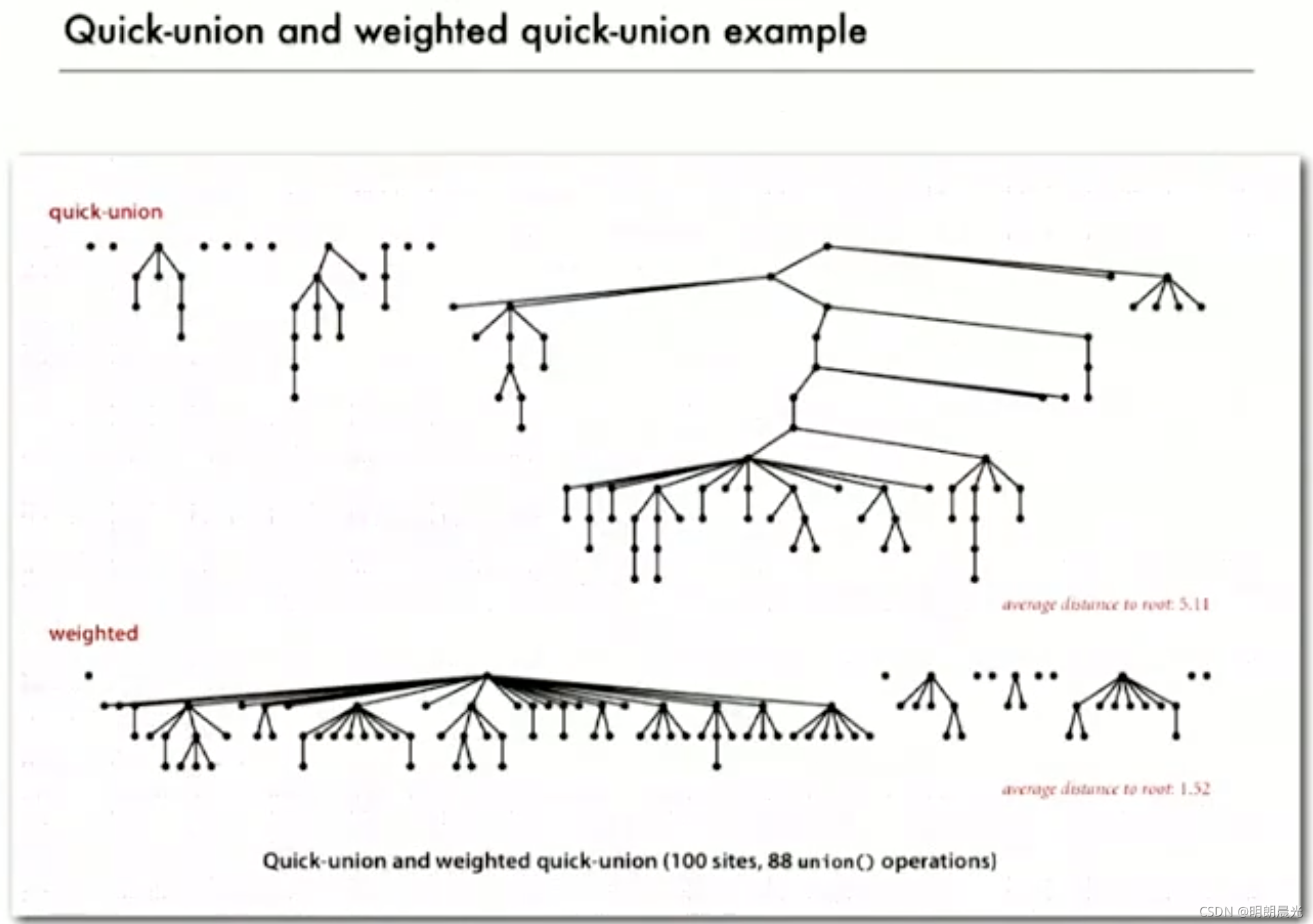
Quick-union 中总结中的图对应的weighted quick-union:
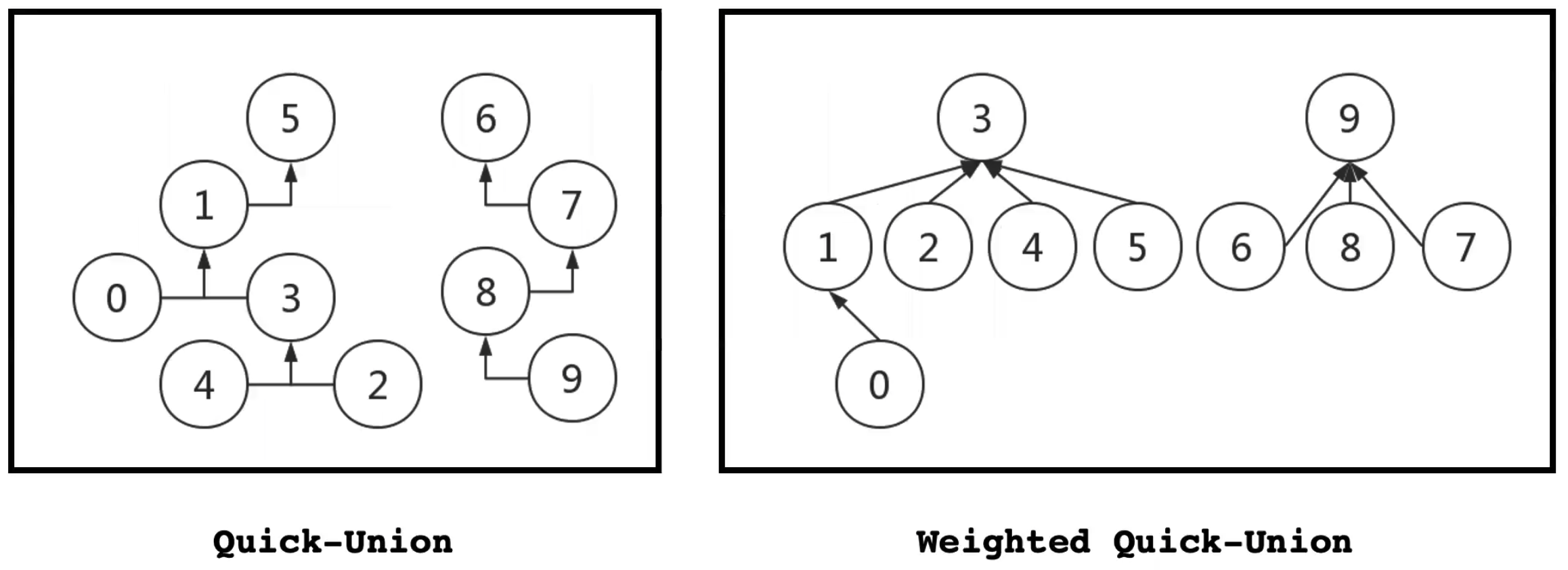
并查集逻辑思维上可以看作是树结构, n 个集合就是 n 棵树,而 n 棵树就是森林。
4.2 代码实现

/*************************************************************************
> File Name: 003.weighted_quick_union.java
> Author: Maureen
> Mail: Maureen@qq.com
> Created Time: 四 10/ 7 21:46:29 2021
************************************************************************/
public class WeightedQuickUnionUF
{
private int[] id; //parent link (site indexed)
private int[] sz; // size of component for roots (site indexed)
private int count; // number of components
public WeightedQuickUnionUF(int n)
{
count = n;
id = new int[n];
for (int i = 0; i < n; i++) id[i] = i;
sz = new int[n];
for (int i = 0; i < n; i++) sz[i] = 1;
}
public int count()
{
return count;
}
public boolean connected(int p, int q)
{
return find(p) == find(q);
}
private int find(int p)
{
//Follow links to find a root.
while (p != id[p]) p = id[p];
return p;
}
public void union(int p, int q)
{
int i = find(p);
int j = find(q);
if (i == j) return ;
//Make smaller root point to larger one.
if (sz[i] < sz[j]) { idp[i] = j; sz[j] += sz[i]; }
else { id[j] = i; sz[i] += sz[j]; }
count--;
}
}
/*************************************************************************
> File Name: 004.weighted_quick_union.c
> Author: Maureen
> Mail: Maureen@qq.com
> Created Time: 四 10/ 7 21:53:50 2021
************************************************************************/
#include <stdio.h>
#include <stdlib.h>
typedef struct UnionSet {
int *father;
int *size; //每个节点下的节点个数
int n;
} UnionSet;
UnionSet *init(int n) {
UnionSet *u = (UnionSet *)malloc(sizeof(UnionSet));
u->father = (int *)malloc(sizeof(int) * (n + 1));
u->size = (int *)malloc(sizeof(int) * (n + 1));
u->n = n;
for (int i = 1; i <= n; i++) {
u->father[i] = i;
u->size[i] = 1;
}
return u;
}
int find(UnionSet *u, int x) {
if (u->father[x] == x) return x;
return find(u, u->father[x]);
}
int merge(UnionSet *u, int a, int b) {
int fa = find(u, a);
int fb = find(u, b);
if (fa == fb) return 0;
if (u->size[fa] < u->size[fb]) {
u->father[fa] = fb;
u->size[fb] += u->size[fa];
} else {
u->father[fb] = fa;
u->size[fa] += u->size[fb];
}
return 1;
}
void clear(UnionSet *u) {
if (u == NULL) return ;
free(u->father);
free(u->size);
free(u);
return ;
}
int main() {
int n, m;
scanf("%d%d", &n, &m);
UnionSet *u = init(n);
for (int i = 0; i < m; i++) {
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
switch (a) {
case 1: merge(u, b, c); break;
case 2: printf("%s\n", find(u, b) == find(u, c) ? "Yes" : "No"); break;
}
}
clear(u);
return 0;
}
正确性可以提交 #71. 练习题1:朋友圈 验证。
4.3 总结
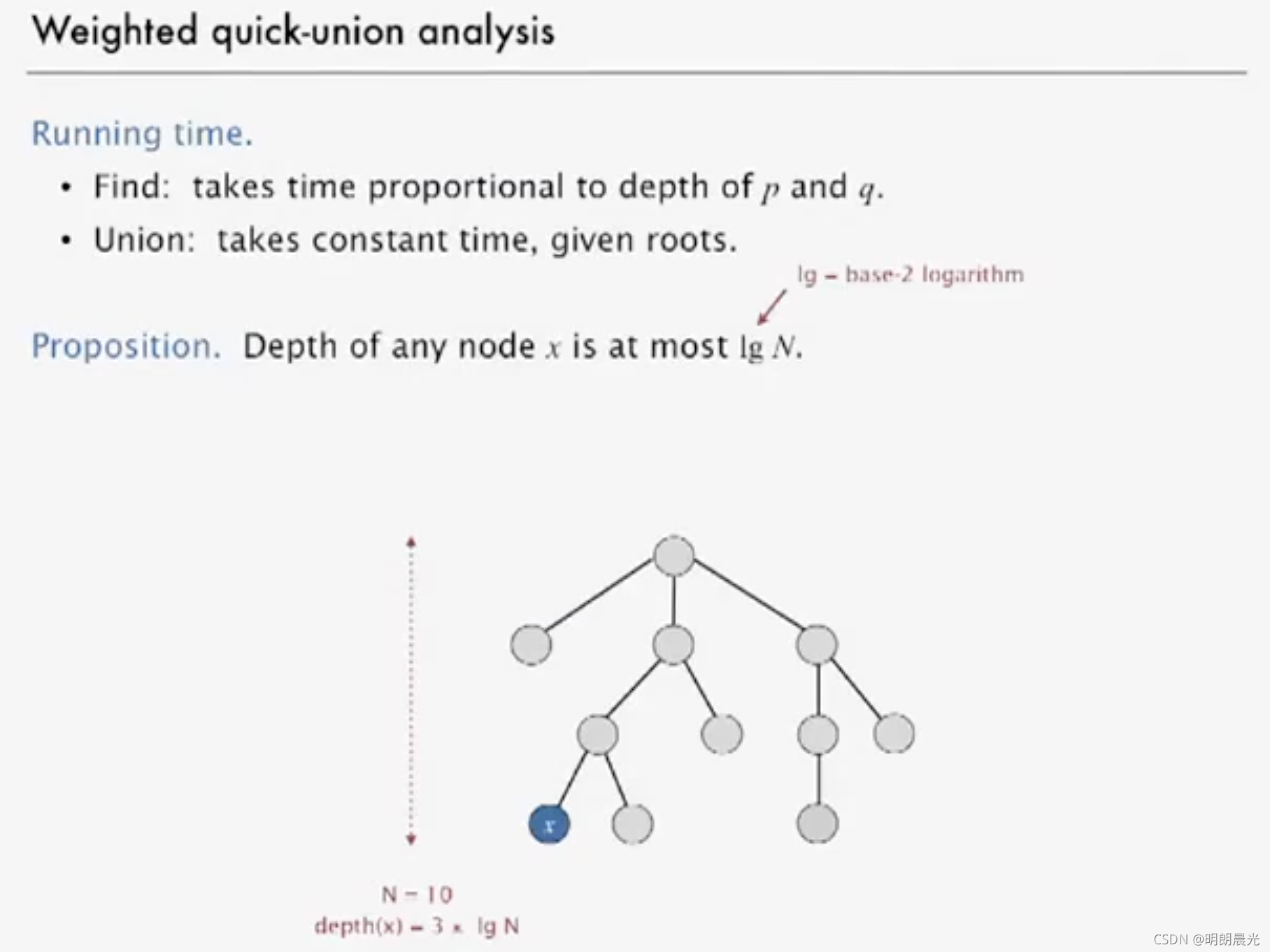


- 连通判断: l o g ( n ) log(n) log(n)
- 合并操作: l o g ( n ) log(n) log(n)
问题最终优化:参考 quick-find 算法,做【路径压缩】
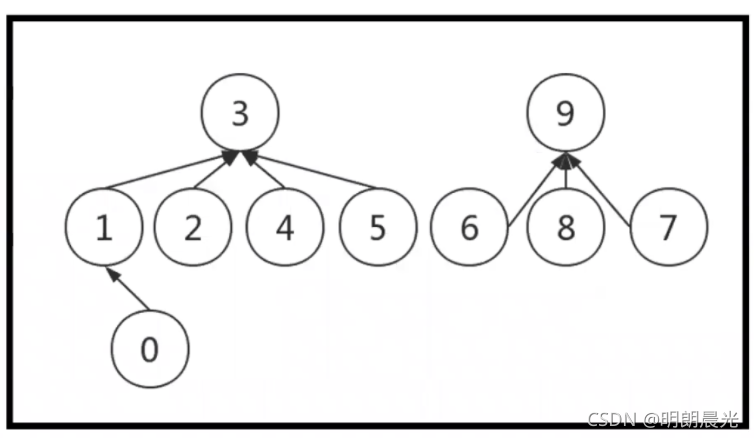
可以将 0 号节点的父节点直接修改为根 3号元素,这就叫路径压缩。路径压缩一般是在连通判断的时候不断向上去做的。
5. Weighted Quick-union with path compression
5.1 讲解
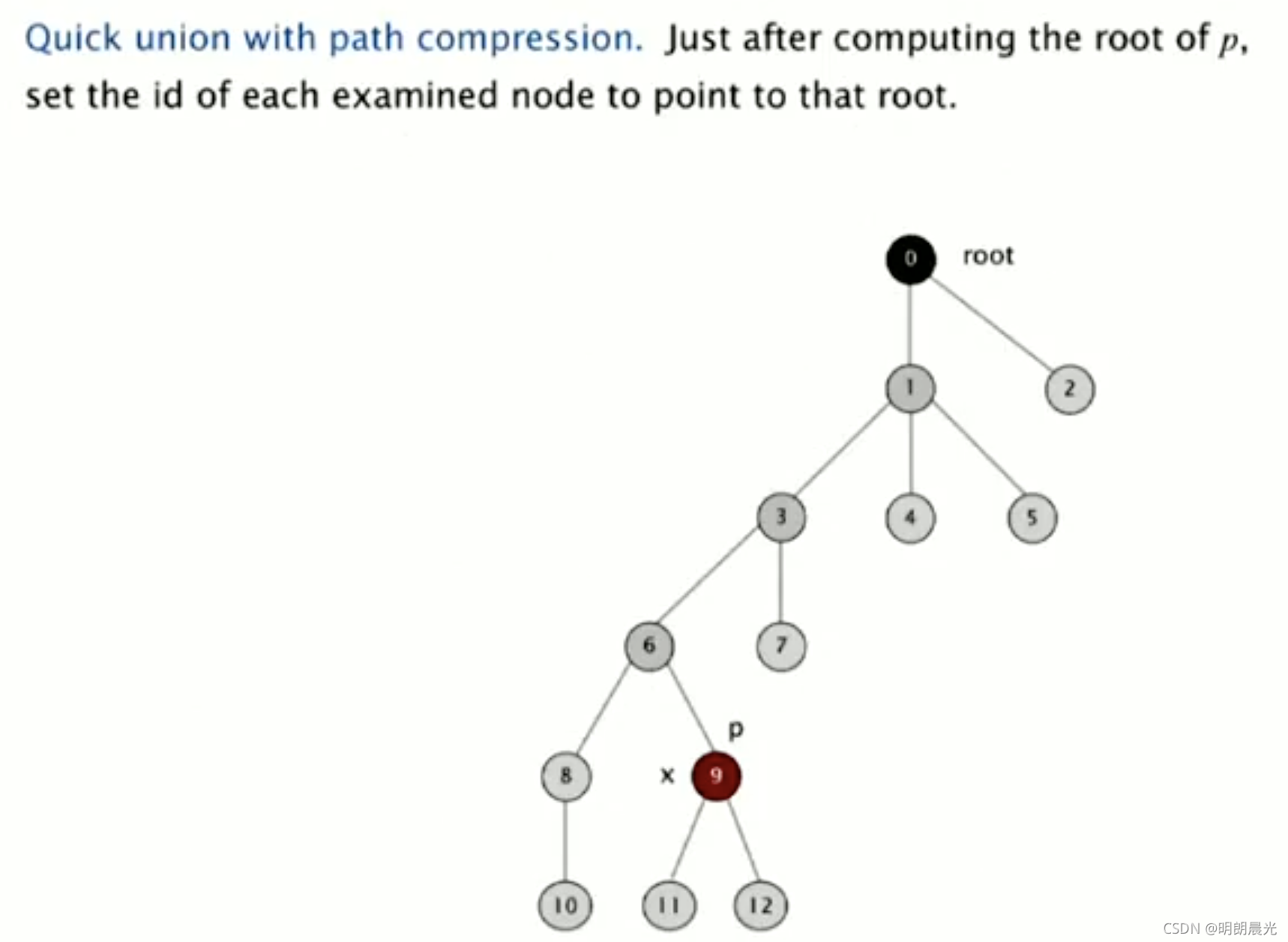
将从 p 到根的经过的每个节点的id 设置为根。
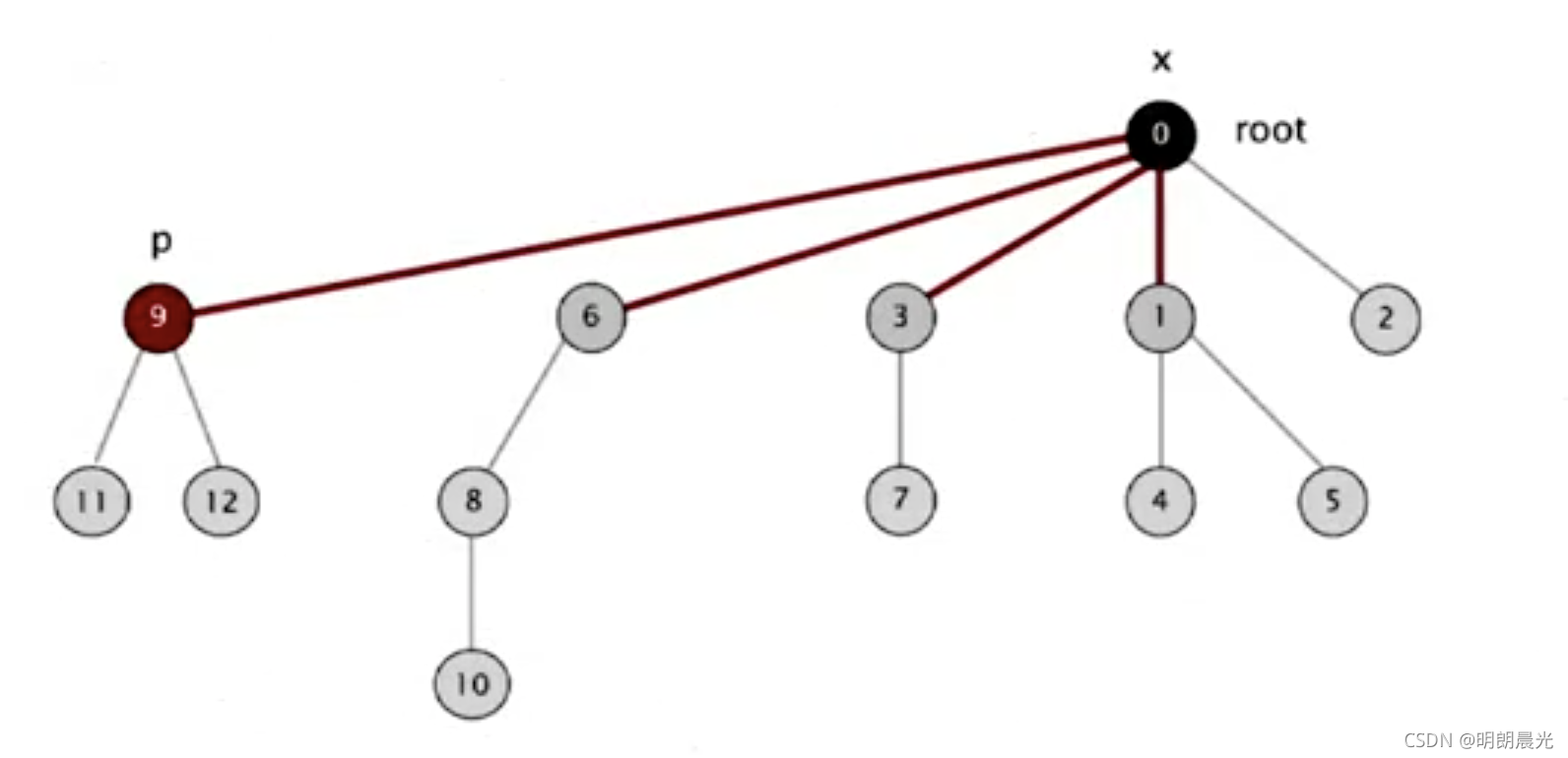
5.2 代码实现

/*************************************************************************
> File Name: 004.weighted_quick_union_with_path_compression.java
> Author: Maureen
> Mail: Maureen@qq.com
> Created Time: 四 10/ 7 22:18:10 2021
************************************************************************/
public class WeightedQuickUnionWithPathCompressionUF
{
private int[] id;
private int[] sz;
private int count;
public WeightedQuickUnionWithPathCompressionUF(int n)
{
count = n;
id = new int[n];
for (int i = 0; i < n; i++) id[i] = i;
sz = new int[n];
for (int i = 0; i < n; i++) sz[i] = 1;
}
public int count()
{
return count;
}
public boolean connected(int p, int q)
{
return find[p] == find[q];
}
private int find(int p)
{
while (p != id[p]) {
id[p] = id[id[p]];
p = id[p];
}
return p;
}
public void union(int p, int q)
{
int i = find(p);
int j = find(q);
if (i == j) return ;
if (sz[i] < sz[j]) { id[i] = j; sz[j] += sz[i]; }
else { id[j] = i; sz[i] += sz[j]; }
count--;
}
}
C语言:
/*************************************************************************
> File Name: 004.weighted_quick_union_with_path_compression.c
> Author: Maureen
> Mail: Maureen@qq.com
> Created Time: 四 10/ 7 22:24:50 2021
************************************************************************/
#include <stdio.h>
#include <stdlib.h>
typedef struct {
int *father;
int *size;
int n; //并查集空间大小
} UnionSet;
UnionSet *init(int n) {
UnionSet *u = (UnionSet *)malloc(sizeof(UnionSet));
u->father = (int *)malloc(sizeof(int) * (n + 1));
u->size = (int *)malloc(sizeof(int) * (n + 1));
u->n = n;
for (int i = 1; i <= n; i++) {
u->father[i] = i;
u->size[i] = 1;
}
return u;
}
int find(UnionSet *u, int x) {
//扁平化,使得x节点直接指向根
return u->father[x] = u->father[x] == x ? x : find(u, u->father[x]);
}
int merge(UnionSet *u, int a, int b) {
int fa = find(u, a), fb = find(u, b);
if (fa == fb) return 0;
if (u->size[fa] < u->size[fb]) {
u->father[fa] = fb;
u->size[fb] += u->size[fa];
} else {
u->father[fb] = fa;
u->size[fa] += u->size[fb];
}
return 1;
}
void clear(UnionSet *u) {
if (u == NULL) return ;
free(u->father);
free(u->size);
free(u);
return ;
}
int main() {
int n, m;
scanf("%d%d", &n, &m);
UnionSet *u = init(n);
for (int i = 0; i < m; i++) {
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
switch (a) {
case 1: merge(u, b, c); break;
case 2: printf("%s\n", find(u, b) == find(u, c) ? "Yes" : "No"); break;
}
}
clear(u);
return 0;
}
正确性可以提交 #71. 练习题1:朋友圈 验证。
实际处理并查集的问题时,不需要进行按秩合并,所以去掉代码中 merge 函数内的按秩优化部分,而是直接使用路径优化,这样可节省一倍的空间:
/*************************************************************************
> File Name: 005.weighted_quick_union_with_path_compression_optimize.c
> Author: Maureen
> Mail: Maureen@qq.com
> Created Time: 四 10/ 7 22:24:50 2021
************************************************************************/
#include <stdio.h>
#include <stdlib.h>
typedef struct {
int *father;
//int *size;
int n; //并查集空间大小
} UnionSet;
UnionSet *init(int n) {
UnionSet *u = (UnionSet *)malloc(sizeof(UnionSet));
u->father = (int *)malloc(sizeof(int) * (n + 1));
// u->size = (int *)malloc(sizeof(int) * (n + 1));
u->n = n;
for (int i = 1; i <= n; i++) {
u->father[i] = i;
// u->size[i] = 1;
}
return u;
}
int find(UnionSet *u, int x) {
//扁平化,使得x节点直接指向根
return u->father[x] = u->father[x] == x ? x : find(u, u->father[x]);
}
int merge(UnionSet *u, int a, int b) {
int fa = find(u, a), fb = find(u, b);
if (fa == fb) return 0;
/*if (u->size[fa] < u->size[fb]) {
u->father[fa] = fb;
u->size[fb] += u->size[fa];
} else {
u->father[fb] = fa;
u->size[fa] += u->size[fb];
}*/
u->father[fb] = fa;
return 1;
}
void clear(UnionSet *u) {
if (u == NULL) return ;
free(u->father);
//free(u->size);
free(u);
return ;
}
int main() {
int n, m;
scanf("%d%d", &n, &m);
UnionSet *u = init(n);
for (int i = 0; i < m; i++) {
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
switch (a) {
case 1: merge(u, b, c); break;
case 2: printf("%s\n", find(u, b) == find(u, c) ? "Yes" : "No"); break;
}
}
clear(u);
return 0;
}
正确性可以提交 #71. 练习题1:朋友圈 验证。
5.3 总结

6. 总结

Weighted quick-union with path compression 算法将运算的时间从 30年减少到了 6s。

quick-union 算法是不稳定的,如果退化成一条链,时间复杂度就是
O
(
n
)
O(n)
O(n)。
路径压缩算法的合并和查找的时间复杂度都趋近为
O
(
1
)
O(1)
O(1),路径压缩是最常用的算法。
7. 相关题目
| 题目 | 难度 |
|---|---|
| Leetcode 128. 最长连续序列 | 中等 |
| Leetcode 130. 被围绕的区域 | 中等 |
| Leetcode 200. 岛屿数量 | 中等 |
| Leetcode 547. 省份数量 | 中等 |
| Leetcode 684. 冗余连接 | 中等 |
| Leetcode 685. 冗余连接 II | 困难 |