数字签名标准(Digital Signature Standard,DSS)是美国公布的联邦信息处理标准,采用SHA和一种新的签名技术的标准称为DSA
DSS的基本方式
DSS的签名方式使用的算法只能提供数字签名功能,不像RSA,RSA的签名方式使用的RSA算法既能用于加密和签名,也能用于密钥交换。
RSA签名过程
签名产生:将消息输入到一个哈希函数以产生一个固定长度的安全哈希值,再用发送方的私钥加密哈希值得到对消息的签名。
验证过程:消息及其签名一起被发送给收方,接收方得到消息后再产生出消息的哈希值,且使用发送方的公钥对收到的签名解密。这样收方就得到了两个哈希值,比较两个哈希值,若值一样,则收到的签名是有效的
过程如图所示:

DSS签名过程
签名产生:DSS签名也使用一个哈希函数产生消息的一个哈希值,将哈希值、随机数k、发方的私钥SKA和全局公钥PKG一起作为签名函数的输入,得到签名函数的两个输出s和r就构成了消息的签名(s,r)。
验证过程:收方收到消息后产生出消息的哈希值,将哈希值、收到的签名、全局公钥PKG和发方的公钥PKA作为验证函数的输入,验证函数的输出如果和收到的签名成分r相等,则收到的签名是有效的
过程如图所示:

数字签名算法DSA
DSA是在ElGamal和Schnorr两个签名方案的基础上设计的,其安全性基于求离散对数的困难性。算法如下:
全局公钥
p:满足2L-1<p<2L的大素数,其中512≤L≤1024,且L是64的倍数
q:p-1的素因子,满足2159<p<2160,即q长为160比特
g:g≡h(p-1)/q mod p,其中h是满足1<h<p-1且使得h(p-1)/q mod p >1的任一整数
用户私钥x
x是满足0<x<q的随机数或伪随机数
用户公钥y
y≡gx mod p
用户为待签消息选取的秘密数k
k满足0<k<q的随机数或伪随机数
签名过程
用户对消息M的签名为(r,s),其中r≡(gx mod p) mod q,s≡[k-1(H(M)+xr)] mod q,H(M)是由SHA求出的哈希值
验证过程
设收方收到的消息为M’,签名为(r’,s’),计算
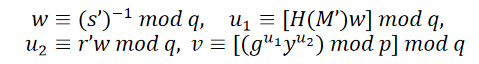
检查v和r’是否相等,若相等,则证明签名有效。其中的四个函数分别为:
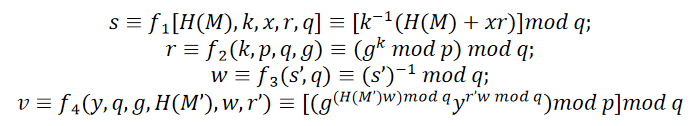
DSA过程如图:

签名产生过程中的运算主要是求r的模指数运算r=(gkmod p)mod q,而这一运算与待签消息无关,因此能被预先计算。事实上,用户可以预先计算出很多r和k-1以备以后的签名使用,从而可大大加快产生签名的速度