/*仅当作学习笔记,若有纰漏欢迎友好交流指正,此外若能提供一点帮助将会十分荣幸*/
本系列谈论过单时滞,但还没提及过双时滞,本文将着重介绍一种双时滞系统并对其进行简单处理分析。
摘 要:本文针对一个捕食网络,根据其特性建立起一个双时滞四维系统。首先分析其稳定性,找到其正平衡点,然后通过调试时滞量τ来模拟预测网络模型的发展前景。并根据所求得临界滞量τ0,带入实值仿真出其Hopf分岔图形。
0引言
自然界中,广泛存在着种群之间的捕食与被捕食关系,他们一起构成了生物链,为流传的“大鱼吃小鱼,小鱼吃虾米”就通俗易懂的道出了生物链之间的关系。而为了保护生态链的完整,甚至保证整个生态系统的有序发展,对其中捕食系统的研究就存在相当的意义。
在捕食系统中,最经典的就是Lotka-Volterra捕食模型(简称L-V模型),其模型方程为:
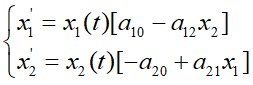
?
-V模型中,x1(t)、x2(t)分别表示再t时刻食饵和捕食者的密度,而x1、x2则分别表示食饵和捕食者在t时刻的种群密度变化量。a10代表食饵种群内自然增长率、a12代表捕食者对食饵捕食的所造成的影响(或者说威胁)、a20代表捕食者种群内部因素带来的数量变化,比如生老病死亦或同族之间的相互争斗带来的影响、a21代表食饵对捕食者所提供的积极影响,即提供食物来源[2]。
显而易见,L-V模型相当的粗略,考虑的因素也很少。因此,在此基础上本文通过增加模型的维数,来加长食物链的长度;通过加入更多系数来模拟捕食者捕食时间、捕食者成长期等因素的影响。试图通过考虑到更多的因素来提高模型的真实性,然后可以人为的调整控制因素来使生物链达到一个动态平衡,即达到一个良性。
1.建立系统模型
自然界中,广泛存在着种群之间的捕食与被捕食关系,他们一起构成了生物链,为流传的“大鱼吃小鱼,小鱼吃虾米”就通俗易懂的道出了生物链之间的关系。而为了保护生态链的完整,甚至保证整个生态系统的有序发展,对其中捕食系统的研究就存在相当的意义。
根据实际情况,并借鉴文献[1]我们这里设置的捕食模型应该具备如下前提条件:

?该双时滞的四维捕食模型为:

在该模型中,x1(t)、x2(t)、x3(t)、x4(t)分别代表一二三级食饵,和食物链顶端的捕食者。其中,一级食饵为食物链最低端,会被二级食饵捕食,二三级食饵以此类推(即生物链的概念,但捕食者只捕食比自己低一级的食饵,这里不考虑跨级捕食)。
而dx1/dt、dx2/dt、dx3/dt、dx4/dt分别代表一二三级食饵,和食物链顶端的捕食者在时刻的数量变化情况。
1.1参数设置
①对一级食饵,即x1(t)而言:

?②对二级食饵,即x2(t)而言:

?③对三级食饵,即x3(t)而言

?④对最高级捕食者,即x4(t)而言

?⑤而对于时间常数τ

1.2约束条件

?
2.正平衡点及稳定性分析
求正平衡点,即各个种群之间的发展达到一个动态平衡,也就是各个种群的数量达到一个稳态值,变化量为0,即
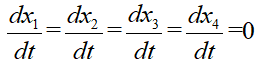
2.1初始条件下的正平衡点
我们设平衡点为E*由于各个种群的变化率为0,由上文中的模型可得:

求解该方程组,我们可以用到solve函数来求解,其对应程序如下:?
%计算正平衡点
syms x1 x2 x3 x4%定义自变量
syms a10 a11 a12 a20 a22 a21 a23 a30 a33 a32 a34 a40 a43%定义系数
[solx1,solx2,solx3,solx4]=solve(x1*(a10-a11*x1-a12*x2)==0,x2*(-a20-a22*x2+a21*x1-a23*x3)==0,x3*(-a30-a33*x3+a32*x2-a34*x4)==0,x4*(-a40+a43*x3)==0,x1,x2,x3,x4)
solutions=[solx1,solx2,solx3,solx4]%方程组
m=double(solx1)%x1*的值
y=double(solx2)%x2*的值
z=double(solx3)%x3*的值
h=double(solx4)%x4*的值
?由于x1*、x2*、x3*、x4*均为非负,因此为了表达的简洁,这里只把符合条件的解列出来:

?可以看出,符合条件的解就只有一组,因此这也佐证了该系统只有唯一的一个正平衡点E*
2.2特征矩阵求解
利用solve函数可以求得模型(1)的雅可比矩阵,其程序为:
%计算正平衡点
syms x1 x2 x3 x4%定义自变量
x=[x1,x2,x3,x4]
syms a10 a11 a12 a20 a22 a21 a23 a30 a33 a32 a34 a40 a43%定义系数
f=[a10*x1-a11*x1^2-a12*x1*x2,-a20*x2-a22*x2^2+a21*x1*x2-a23*x2*x3,-a30*x3-a33*x3^2+a32*x2*x3-a34*x3*x4,-a40*x4+a43*x3*x4]%定义函数,以矩阵形式展示
j=jacobian(f,x)%计算雅可比矩阵但上述公式并未考虑到时滞因素τ,加上时滞因素后,求得模型(1)的完整雅可比矩阵为:

?由雅可比矩阵可以推出其对应特征矩阵X为:

通过特征矩阵X我们又可以推出其特征方程(其中为了在MATLAB里表示方便,τ用y代替),这里可以用到det和collect函数,其具体程序为:?
%求特征方程
syms x1 x2 x3 x4%定义自变量
syms a10 a11 a12 a20 a22 a21 a23 a30 a33 a32 a34 a40 a43 y t1 t2 e%定义系数
f=[-a11*x1,-a12*x1*e^(-y*t1),0,0;a21*x2*e^(-y*t2),-a22*x2,-a23*x2*e^(-y*t1),0;0,a32*x3*e^(-y*t2),-a33*x3,-a34*x3*e^(-y*t1);0,0,a43*x4*e^(-y*t2),0];
m=det(f)%计算矩阵
k=collect(m,y)%得特征方程
?根据初始条件τ=τ1+τ2,将计算结果整合可得出其特征方程为:

?其中:

?
2.3稳定性分析
2.3.1 τ1=τ2=τ=0时
特征方程(2)可以改写为:
![]()
根据文献[3]对正平衡点的初值情况分析思路,我们可得以劳斯-赫尔维茨判据为依据,对于四阶方程来说,为了保证特征方程M的系统稳定,即本文的系统(1)。其需要满足假设H1:

?
2.3.2存在一个临界τ0,使得τ2=τ0-τ1
即假设存在一个临界滞量τ0,使得当τ在τ0附近取值时(但τ<τ0),系统(1)仍稳定。这里就近似的把系统(1)转化为一个单时滞系统。
τ>0,假设λ=iw(w>0)作为特征方程(2)的一个纯虚根带入(2)中,分离出实部和虚部,得:

?根据上式,整理出sinwτ和coswτ的表达式:

?其中:
?
?


2.4 总结

3.仿真
3.1参数设置

?
3.2系数求解
在正平衡点E*处,将参数带入模型(1)中得:

求解上式方程组,对应程序为:
syms S L A M
[solS,solL,solA,solM]=solve(S*(1.4-0.2*S-0.4*L)==0,L*(-0.2-0.2*L+0.3*S-0.4*A)==0,A*(-0.2-0.2*A+0.3*L-0.4*M)==0,M*(-0.2+0.3*A)==0,S,L,A,M)%列出方程组
solutions=[solS,solL,solA,solM]
x1=double(solS)%x1*的值
x2=double(solL)%x2*的值
x3=double(solA)%x3*的值
x4=double(solM)%x4*的值
?得:

从上述众多组解中,由于x*均大于0,则取最后一组解(并化为小数形式),即:?

?3.3结果仿真
![]()

?
?程序:
clear;clc;
%--------------------------------------------------------------------
% 参数设置
%--------------------------------------------------------------------
a10=1.4;
a11=0.2;
a12=0.4;
a20=0.2;
a22=0.2;
a21=0.3;
a23=0.4;
a30=0.2;
a33=0.2;
a32=0.3;
a34=0.4;
a40=0.2;
a43=0.3;
%初值取平衡点E*
S=2.9197;
L=2.0417;
A=0.6667;
M=0.6979;
T=0:60;
%tao取值
t1=10;
t2=8;
t0=t1+t2;
for idx = 1:length(T)-1
if idx<=t0%第一阶段
S(idx+1)=S(idx)+S(idx)*(a10-a11*S(idx)-a12*L(idx));
L(idx+1)=L(idx)+L(idx)*(-a20-a22*L(idx)+a21*S(idx)-a23*A(idx));
A(idx+1)=A(idx)+A(idx)*(-a30-a33*A(idx)+a32*L(idx)-a34*M(idx));
M(idx+1)=M(idx)+M(idx)*(-a40+a43*A(idx));
elseif idx>t0%第二阶段,时滞开始起作用
S(idx+1)=S(idx)+S(idx)*(a10-a11*S(idx)-a12*L(idx-t1));
L(idx+1)=L(idx)+L(idx)*(-a20-a22*L(idx)+a21*S(idx-t2)-a23*A(idx-t1));
A(idx+1)=A(idx)+A(idx)*(-a30-a33*A(idx)+a32*L(idx-t2)-a34*M(idx-t1));
M(idx+1)=M(idx)+M(idx)*(-a40+a43*A(idx-t2));
end
end
%画出图像
figure
subplot(2,2,1),plot(T,S);
grid on;
xlabel('t');
ylabel('S(t)');
title('x1');
subplot(2,2,2),plot(T,L);
grid on;
xlabel('t');
ylabel('L(t)');
title('x2');
subplot(2,2,3),plot(T,A);
grid on;
xlabel('t');
ylabel('A(t)');
title('x3');
subplot(2,2,4),plot(T,M);
grid on;
xlabel('t');
ylabel('M(t)');
title('x4');
?4结论

5参考文献
- 武利青,王晓云.一类具有双时滞四维捕食模型的定性分析.中北大学学报:自然科学版,2019(2):97-102.
- 李大虎,陈淑苹,童欢,朱文文.具有捕食者相互残杀项双时滞系统的Hopf分支.湖北师范学院学报:自然科学版,2011,31(3):76-80.
- 李颖. HR神经元模型的正平衡点稳定性分析.甘肃科技纵横,2017.01.022
- Yang, LX Yang, XF. Propagation Behavior of Virus Codes in the Situation That Infected Computers Are Connected to the Internet with Positive Probability.[J].Discrete Dynamics in Nature and Society,2012,(1):1-13