0-1背包问题

dp[i][w]表示,对于前i个物品,当背包容量为w的时候,所能获得的最大价值
对于是否装第i个物品.有两个状态:
如果不装入第i个物品,dp[i][w]=dp[i-1][w]
如果装入第i个物品,dp[i][w]=dp[i-1][w-wt[i-1]]+val[i-1]
子集背包问题
416--分割等和子集

?转化为背包问题,对数组进行求和,如果能分成等和子集,那么就是求是否能用他的元素凑成sum/2
public boolean canPartition(int[] nums) {
int sum=0;
for (int num : nums) {
sum+=num;
}
if(sum%2!=0)return false;
int target=sum/2;
int n=nums.length;
boolean[][] dp = new boolean[n+1][target+1];
for (int i = 0; i <=n ; i++) {
dp[i][0]=true;//当背包没有空间的时候就相当于装满了
}
for (int i = 1; i <=n; i++) {
for (int j = 1; j <= target; j++) {
//背包的容量不足
if(j-nums[i-1]<0){
dp[i][j]=dp[i-1][j];
}else{
//如果不装入背包的情况已经为true了,那么认为它自己也是true
//也可以理解为放入背包和不放入背包的两种情况之和
dp[i][j]=dp[i-1][j-nums[i-1]]||dp[i-1][j];
}
}
}
return dp[n][target];
}对该代码进行压缩处理:唯一需要注意的是 j 应该从后往前反向遍历,因为每个物品(或者说数字)只能用一次,以免之前的结果影响其他的结果。
public boolean canPartition(int[] nums) {
int sum = 0;
for (int num : nums) {
sum += num;
}
if (sum % 2 != 0) return false;
int target = sum / 2;
int n = nums.length;
boolean[] dp = new boolean[target + 1];
//base
dp[0]=true;
for (int i = 1; i <=n ; i++) {
for (int j = target; j >= 0; j--)
if (j - nums[i-1] >= 0)
dp[j] = dp[j]||dp[j - nums[i-1]];
}
return dp[target];
}518--零钱兑换

?base case 为 dp[0][..] = 0, dp[..][0] = 1。因为如果不使用任何硬币面值,就无法凑出任何金额;如果凑出的目标金额为 0,那么“无为而治”就是唯一的一种凑法。
如果你不把这第 i 个物品装入背包,也就是说你不使用 coins[i] 这个面值的硬币,那么凑出面额 j 的方法数 dp[i][j] 应该等于 dp[i-1][j],继承之前的结果。
如果你把这第 i 个物品装入了背包,也就是说你使用 coins[i] 这个面值的硬币,那么 dp[i][j] 应该等于 dp[i][j-coins[i-1]]。
dp[i][j-coins[i-1]] 表示如果你决定使用这个面值的硬币,那么就应该关注如何凑出金额 j - coins[i-1]。
优化前
public int change(int amount, int[] coins) {
int n=coins.length;
int[][] dp = new int[n+1][amount+1];
for (int i = 0; i <=amount ; i++) {
dp[0][i]=0;
}
for (int i = 0; i <=n; i++) {
dp[i][0]=1;
}
for (int i = 1; i <=n ; i++) {
for (int j = 1; j <=amount ; j++) {
if(j-coins[i-1]<0){
dp[i][j]=dp[i-1][j];
}else{
//放入背包或者不放入背包
dp[i][j]=dp[i][j-coins[i-1]]+dp[i-1][j];
}
}
}
return dp[n][amount];
}压缩后
public int change(int amount, int[] coins) {
int n=coins.length;
int[] dp = new int[amount+1];
dp[0]=1;
for (int i = 1; i <=n ; i++) {
for (int j=1; j<=amount ; j++) {
if(j-coins[i-1]>=0){
dp[j]=dp[j]+dp[j-coins[i-1]];
}
}
}
return dp[amount];
}贪心算法?
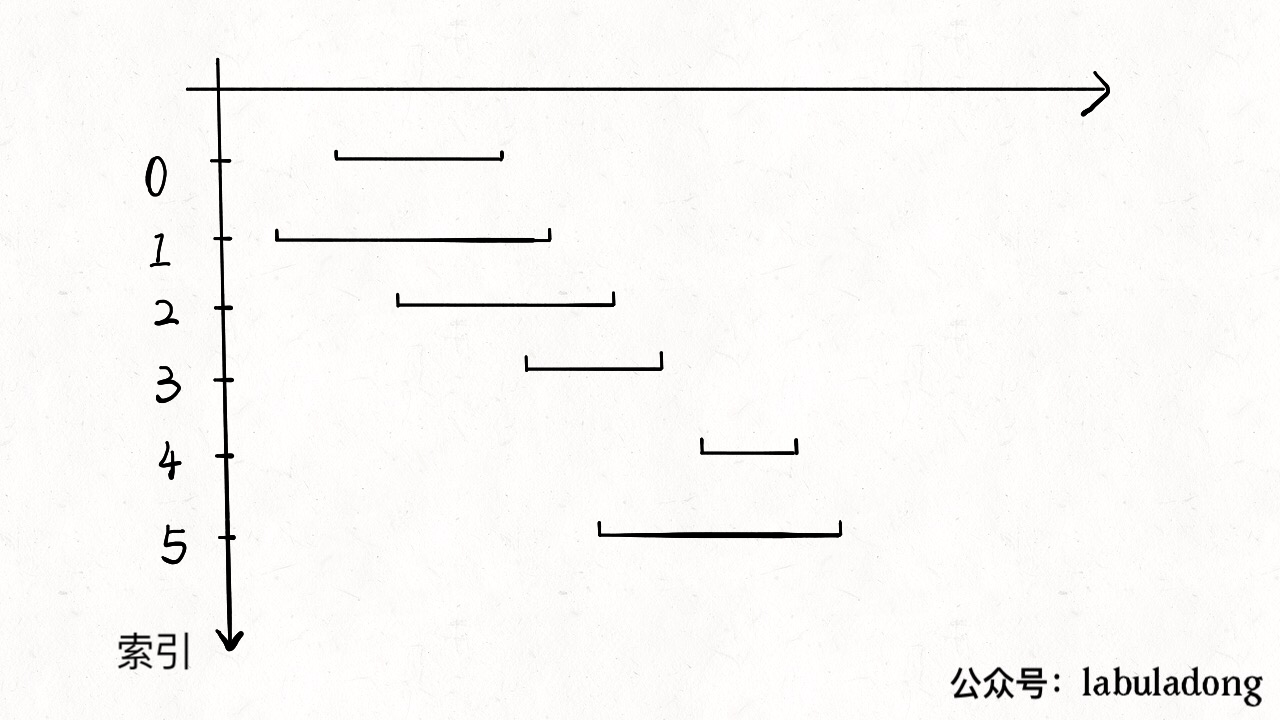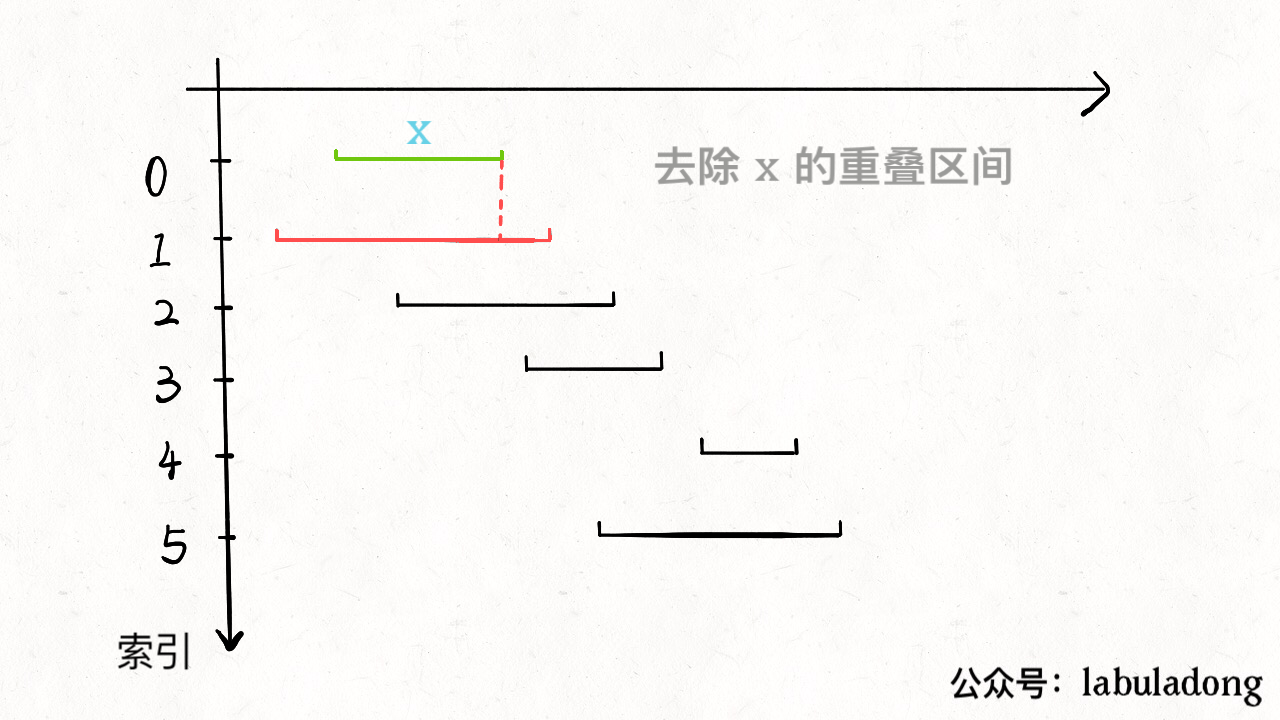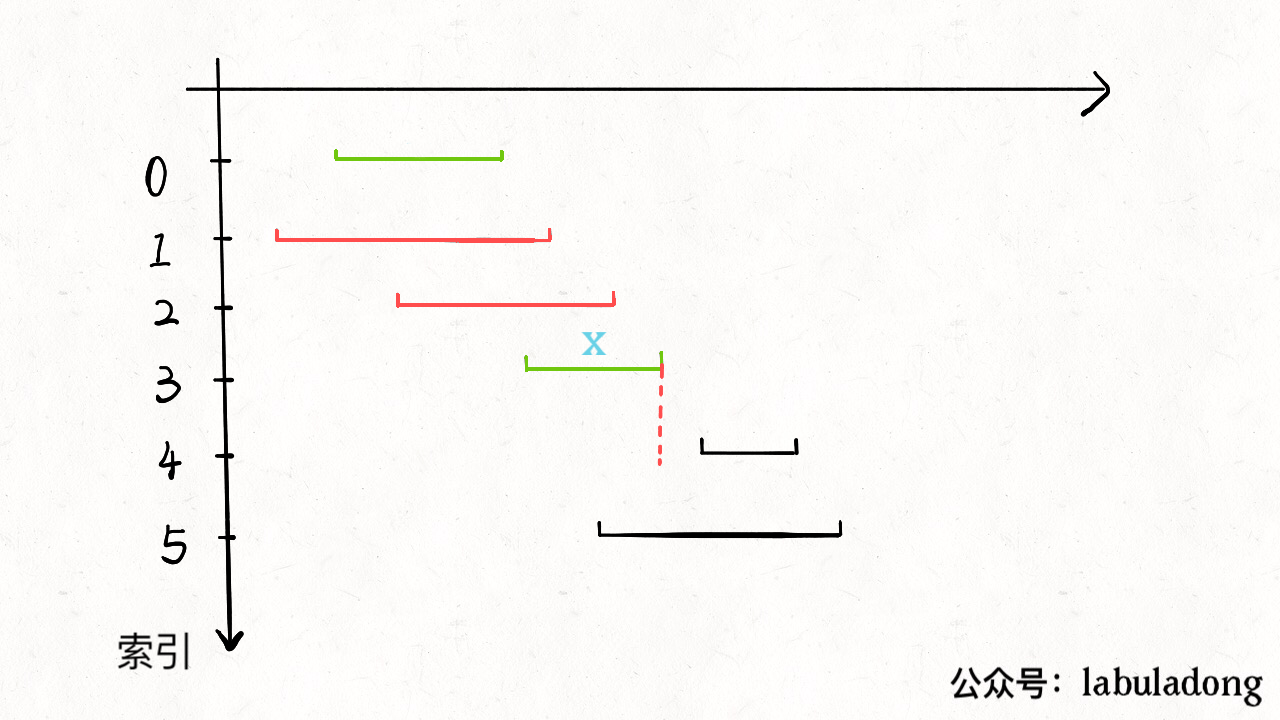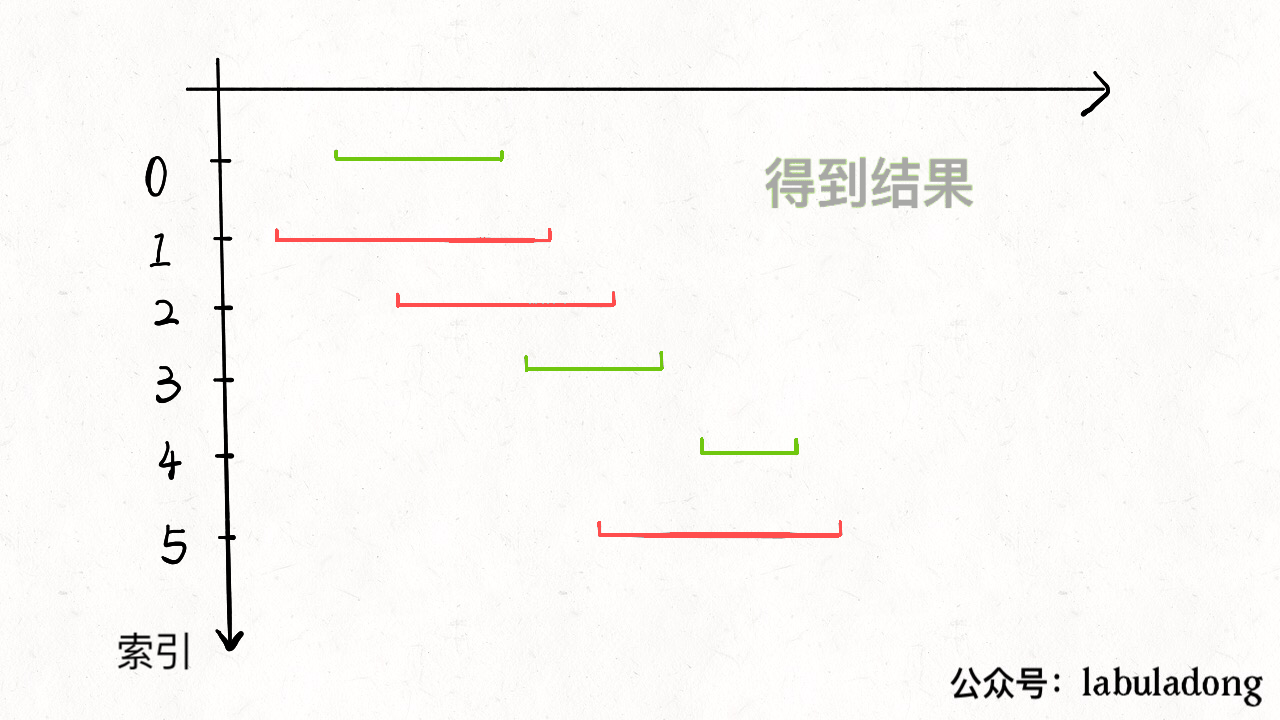
435--无重叠区间

按照区间的end进行排序,从最小的开始作为x,以end为基准,找到start比end大的区间称为下一个x,start比end小就直接删除
public int eraseOverlapIntervals(int[][] intervals) {
Arrays.sort(intervals,(a,b)->{
return a[1]-b[1];
});
//表示最后不相交的区间数
int res=1;//初始的时候就已经存在一个区间了
int now=intervals[0][1];
for (int i = 1; i < intervals.length; i++) {
if(intervals[i][0]>=now){
now=intervals[i][1];
res++;
}
}
return intervals.length-res;
}?452--重叠子区间问题,射气球

?需要注意的是,这题的范围和上题不同,在排序的时候直接相减是又可能导致整形溢出的


public int findMinArrowShots(int[][] points) {
Arrays.sort(points,(p1,p2)->{
return Integer.compare(p1[1],p2[1]);
});
int res=1;
int now=points[0][1];
for (int i = 1; i < points.length; i++) {
if(points[i][0]>now){//触碰边界也会爆炸,不加=
res++;
now=points[i][1];
}
}
return res;
}?253--会议室
 ?每次遇到红色的点,count+1,遇到绿色的点count-1,选取最少的会议室就是选择count的最大值
?每次遇到红色的点,count+1,遇到绿色的点count-1,选取最少的会议室就是选择count的最大值
int minMeetingRooms(int[][] meetings) {
int n = meetings.length;
int[] begin = new int[n];
int[] end = new int[n];
for(int i = 0; i < n; i++) {
begin[i] = meetings[i][0];
end[i] = meetings[i][1];
}
Arrays.sort(begin);
Arrays.sort(end);
// 扫描过程中的计数器
int count = 0;
// 双指针技巧
int res = 0, i = 0, j = 0;
while (i < n && j < n) {
if (begin[i] < end[j]) {
// 扫描到一个红点
count++;
i++;
} else {
// 扫描到一个绿点
count--;
j++;
}
// 记录扫描过程中的最大值
res = Math.max(res, count);
}
return res;
}?1024--视频剪辑

看到区间问题就要想到要使用起点或者终点来进行排序,对于起点的升序排列,每次选择终点走的最远的,当两者相同的时候,选择按照终点降序排列

public int videoStitching(int[][] clips, int time) {
int n=clips.length;
Arrays.sort(clips, (a, b) -> {
return a[0] == b[0] ? Integer.compare(b[1], a[1]) : Integer.compare(a[0], b[0]);
});
int i=0, curEnd=0,nextEnd=0,res=0;
//当起点比currentEnd小的时候
while (i<n&&clips[i][0]<=curEnd){
//贪心的选择下一个视频
while (i<n&&clips[i][0]<=curEnd){
nextEnd=Math.max(nextEnd,clips[i][1]);//找到符合条件的最远距离
i++;
}
//超出了curEnd的范围或者超过了数组最大长度
res++;
curEnd=nextEnd;//此时已经不符合条件了
if(curEnd>=time)return res; //仅当超过标准时间时才返回结果
}
return -1;
}?55--跳跃游戏

public boolean canJump(int[] nums) {
int n = nums.length;
int farthest = 0;
for (int i = 0; i < n - 1; i++) {
// 不断计算能跳到的最远距离
farthest = Math.max(farthest, i + nums[i]);
// 最远距离都碰到了0,那确实是跳不动了
if (farthest == i) return false;
}
return farthest >= n - 1;
}45--跳跃游戏2

?备忘录写法:
public class likou45 {
int[] memo;
public int jump(int[] nums) {
int n=nums.length;
memo=new int[n];//到当前索引最少跳的步数
Arrays.fill(memo,n);//相当于无限大
return dp(nums,0);
}
//从索引 i 跳到最后一格,至少需要 dp(nums, i) 步
private int dp(int[] nums, int i) {
int n=nums.length;
if(i>=n-1)return 0;
if(memo[i]!=n){
return memo[i];
}
int steps=nums[i];//当前可以跳跃的步数
for (int j = 1; j <=steps ; j++) {
int subProblem=dp(nums,i+j);
memo[i]=Math.min(memo[i],subProblem+1);//记录子问题
}
return memo[i];
}
}贪心写法:
public int jump(int[] nums) {
int n=nums.length;
int end=0,farthest=0,jumps=0;
for (int i = 0; i < n-1; i++) {
//不断的更新最有潜力的元素
farthest=Math.max(nums[i]+i,farthest);
//end表示每次能跳跃的最远索引
if(end==i){
//到达最远索引处,此时无论如何我们都要跳一步了
jumps++;
//更新下一次截止距离为最有潜力的元素能跳到的最远索引值
end=farthest;
}
}
return jumps;
}134--加油站

对于gas[i]-cost[i]这样一个数组,它的累加值可能如下图,只要把最低点作为起始点,就可以保证一定可以使得整个线段都在x轴之上,也就是不会空油

public int canCompleteCircuit(int[] gas, int[] cost) {
int n= gas.length;
int min=0,start=0, sum=0;
for (int i = 0; i < n; i++) {
sum+=gas[i]-cost[i];
//sum成为新低
if(sum<min){
start=i+1;//经过了i后,sum达到最低,那么i+1就应该成为最新的起点
min=sum;
}
}
//总油量小于总消耗的时候是不能走成循环的
if(sum<0)return -1;
//因为是环形,所以到最后一个索引的时候,应该变成1
return start==n?0:start;
}