文章目录
第一章 绪论
Concepts of Algorithms
-
算法的性质:
- 终止性(有穷性):有限步骤内必须停止
- 确定性:每步都是严格定义和确定的动作
- 能行性:算法的每一步都可以被精确地机械执行
- 输入:具有满足给定约束条件的输入
- 输出:产生满足给定约束条件的结果
-
问题:一个二元组集合,一个二元组包含了输入和输出
-
问题实例:问题中的一个二元组
-
一个算法求解一个完整的问题,可以求解这个问题中所有的二元组,而不是一个或几个
Analyzing Algorithms
算法的正确性分析
-
不正确算法:
1、在一个或多个输入上不停止
2、在一个或多个输入上产生不正确结果 -
近似算法/随机算法的正确性
1、对所有输入都停止
2、产生近似正确的解/产生不多的不正确解
程序调试只能证明程序有错、不能证明程序无错误
算法的复杂性分析
- 是输入大小的函数
1、时间复杂性T(n):是输入大小的函数、该算法对该输入产生结果需要的原子操作数
2、空间复杂性S(n):是输入大小的函数、该算法对该输入产生结果需要的存储空间大小
例:直接插入排序算法的复杂性分析,直接插入排序算法如图:
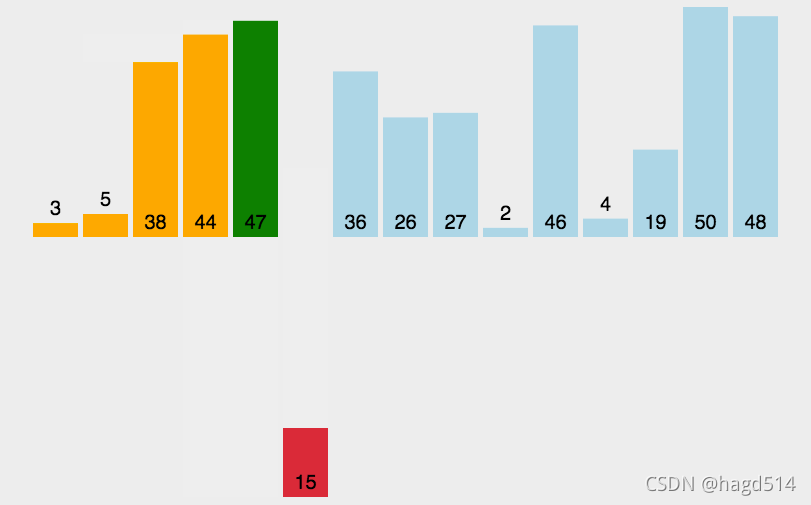
算法的正确性分析
- 循环不变量方法:证明主要结构为循环的算法的正确性
主要步骤:
1、确定循环不变量P(谓词)
2、三个步骤:
- 循环初始:P成立
- 循环步骤:每执行一次、P都成立
- 循环终止:循环结束后、P依旧成立
例:插入排序
1、首先定义循环不变量P。对于任意循环变量j,A[1,…,j-1]中的数据都是有序的
2、再执行三个步骤。发现循环开始前和每一次循环后以及循环彻底结束后,A[1,…,j-1]中的数据都是有序的,即循环不变量恒成立。所以算法正确。
Designing Algorithms
- Divide-and-Conquer——分治算法
- Dynamic Programming——动态规划
- Greedy Algorithms——贪心算法
第二章 算法分析的数学基础
计算复杂性函数的阶
同阶函数
设f(n)和g(n)是正值函数。如果存在c1, c2>0, n0 , 存在n>n0, c1g(n)≤f(n)≤c2g(n),则称f(n)与g(n) 同阶,记作f(n)=θ(g(n))。