[数据结构与算法]二分查找算法的实现（C语言）

在计算机科学中，二分查找（英语：binary search），也称折半查找（英语：half-interval search）、对数搜索（英语：logarithmic search），是一种在有序数组中查找某一特定元素的搜索算法。搜索过程从的数组中间元素开始，如果中间元素正好是要查找的元素，则搜索过程结束；如果某一特定元素大于或者小于中间元素，则在数组大于或小于中间元素的那一半中查找，而且跟开始一样从中间元素开始比较。如果在某一步骤数组为空，则代表找不到。这种搜索算法每一次比较都使搜索范围缩小一半。

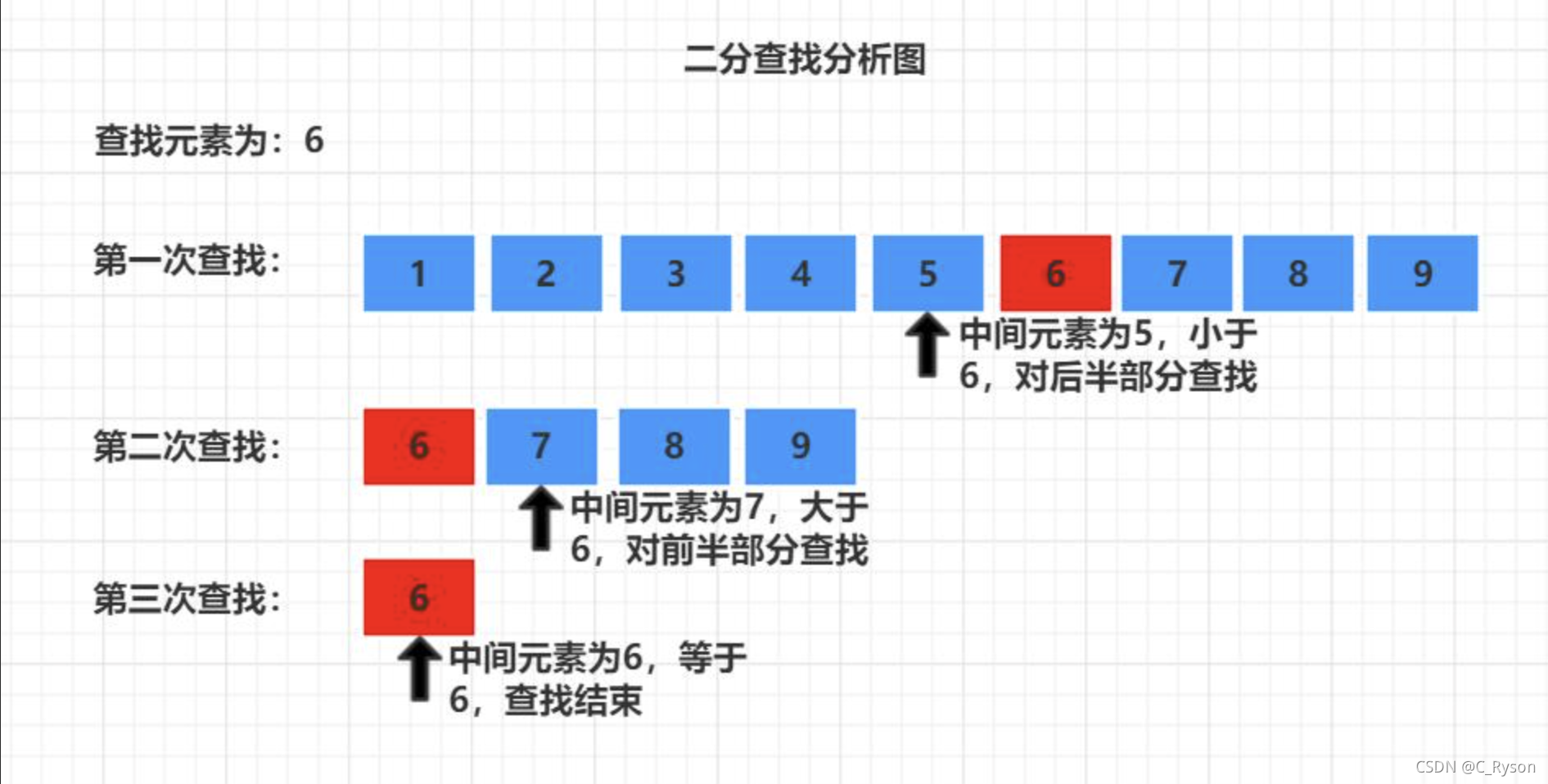
?从上面的简介可以看出，使用二分查找算法的条件有二：

1，有序。2，元素顺序存储，即数组

二分查找的重要思想在于，找到中间的数，将其与左右两边的“界限”做比较，从而再次缩小左右两边的界限，直到找到我们所要的那个元素。

在数组中找一个数，我们最容易想到的就是将其与数组中每一个数作比较，代码实现如下

#include<stdio.h>
int main()
{
   int arr[10]={1,2,3,4,5,6,7,8,9,10};
   int k=0;
   scanf("%d",&k);
   int i=0;
   for(;i<10;i++)
   {
     if(arr[i]==k)
     break;
   }
  if(i<10)
   printf("找到了：下标是%d\n",i);
  else
   printf("找不到");
   return 0;
}

而这样去查找很显然，当要查找的元素在数组的后面时，所消耗的时间会需要很多，这处的例子数组元素较少，而之后若数组元素增大呢？

而二分查找算法就极大提高了查找的效率，每次查找完 都可以排除掉一半的元素，代码实现如下

#include<stdio.h>
int main()
{
	int arr[10] = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 };
	int sz = sizeof(arr) / sizeof(arr[0]);//求数组元素个数
	int k = 0;
	scanf("%d", &k);//输入所要查找的数
	int left = 0;//左界限
	int right = sz-1; //右界限
	while (left <= right)//确保两者之间还有元素可以查找
	{
		int mid = (left + right) / 2;
		if (arr[mid]<k)
			left = mid+1;
		else if (arr[mid]>k)
			right = mid-1;
		else
		{
			printf("找到了，下标是：%d\n", mid);
			break;
		}
	}
	if (left>right)
		printf("找不到\n");
	return 0;
}

记得要用break跳出循环，否则会一直打印。以上就是二分查找算法的实现。

这时候有个问题了，不是顺序的数组怎么办，我又想用二分查找算法来找元素。这个就涉及到排序算法啦，排序算法有多种，之后的博客在慢慢跟大家分享。希望对大家的学习有所帮助。看到这里，不妨点个关注吧，我会坚持更新的。

以上内容，如有错误，请联系修改。

参考资料：

1，二分搜索算法_百度百科 (baidu.com)

2，二分查找算法动图 - 国内版 Bing images（图片来源）