[数据结构与算法]2021CCPC网络赛题解（目前只有10101011，待补充）

1010 Bigraph Extension（思维，构造，并查集维护）

• 题目描述： n 个左部点，n 个右部点。初始有 m 条边，都是左部点与右部点连接的边，且保证不存在顶点相同的边。求最少要添加多少条边，使得任意左部点，任意右部点，其最长简单路径的长度大于 n 。并输出最小字典序连连边 $c_1,d_1,c_2,d_2$ 。数据保证 n 为偶数。$T\in [1,1000]，n\in [2,2000]$
• 问题分析：
• 结论： 结果一定是一个 2n 环。
• 证明： 想要连边最小并且全部连通，显然是 2n-1 条边构成一棵树。但是对于一棵树，树上显然会存在最长简单路径为 1 的路径。不符合题意。考虑添加 2n 条边构成一个环。这样最长简单路径就是 n 了。但是由于 n 是偶数，左部点到右部点的路径不可能是偶数，因此最长简单路径一定是 n+1 ，符合题意。
• 写法： m 条边不存在顶点相同的边，那么其实对正解没有任何影响。w我们拿两个指针 i,j 分别记录左右部点的最小度不为 2 的点即可。但是 i,j 不能直接连接的，还需要考虑 i,j 是否已经在一个并查集里，因为如果已经在一个并查集里，再连边的话：会提前构成环，就无法形成 2n 的大环了。因此需要找到一个度不为 2 的且与 i 不在一个并查集里的 j ，去连边。最后一次的时候再去找度为 1 的左右部点，连接，形成 2n 的大环。

#include<bits/stdc++.h>
using namespace std;
const int N=4e5+10;
int du1[N],du2[N],fa[N];

int find(int x){
	if(x==fa[x])return x;
	else return fa[x]=find(fa[x]);
}
int merge(int x,int y){
	int p1=find(x),p2=find(y);
	if(p1!=p2)fa[p1]=p2;
}
int main() {
	int T,n,m,u,v;
	cin>>T;
	while(T--) {
		cin>>n>>m;

		for(int i=1; i<=n; i++)du1[i]=du2[i]=0;
		for(int i=1;i<=2*n;i++)fa[i]=i;
		
		for(int i=1; i<=m; i++) {
			cin>>u>>v;
			du1[u]++;
			du2[v]++;
			merge(u,v+n);
		}
		cout<<2*n-m<<'\n';
		int i=1,j=1,num=m;
		while(1) {
			while(du1[i]==2)i++;
			while(du2[j]==2)j++;
			int temp=j;
			while(du2[temp]==2||(find(i)==find(temp+n)))temp++;
			du1[i]++;
			du2[temp]++;
			merge(i,temp+n);
			cout<<i<<" "<<temp<<'\n';
			num++;
			if(num==2*n-1)break;
		}
		for(int j=1;j<=n;j++){
			if(du2[j]==1){
				cout<<n<<" "<<j<<'\n';
				break;
			}
		}
	}
	return 0;
}

1011 Jumping Monkey（思维，并查集，差分建图）

• 题目描述： 给定 n 个点的一棵树，树的样子已经给定。每个点都有权值 $a_i$ ，数据保证 $a_i$ 互不相同。点 u 能跳到点 v 的条件是：$a_v$ 是 u 到 v 的这条简单路径上的点权最大值。求对于每个点 $u\in [1,n]$，可以跳到多少个点（起点也算一个点）。$T\in [1,1e4],n\in [1,1e5],\sum n\in [1,8e5],a_i\in [1,1e9]$
• 问题分析： 正着思考很难想。考虑逐渐增加点 u ，求哪些点可以跳到点 u 从而使答案增加。显然逐渐增加点的顺序是点权从小到大。
• 假设枚举到了 u ，考虑 u 的邻接点 v ，如果 $a_v<a_u$ 则显然 $v$ 所在的连通分量均可以走到 u ，从而使答案加 1 。然后将其再连接即可。这个过程我们可以用并查集维护。
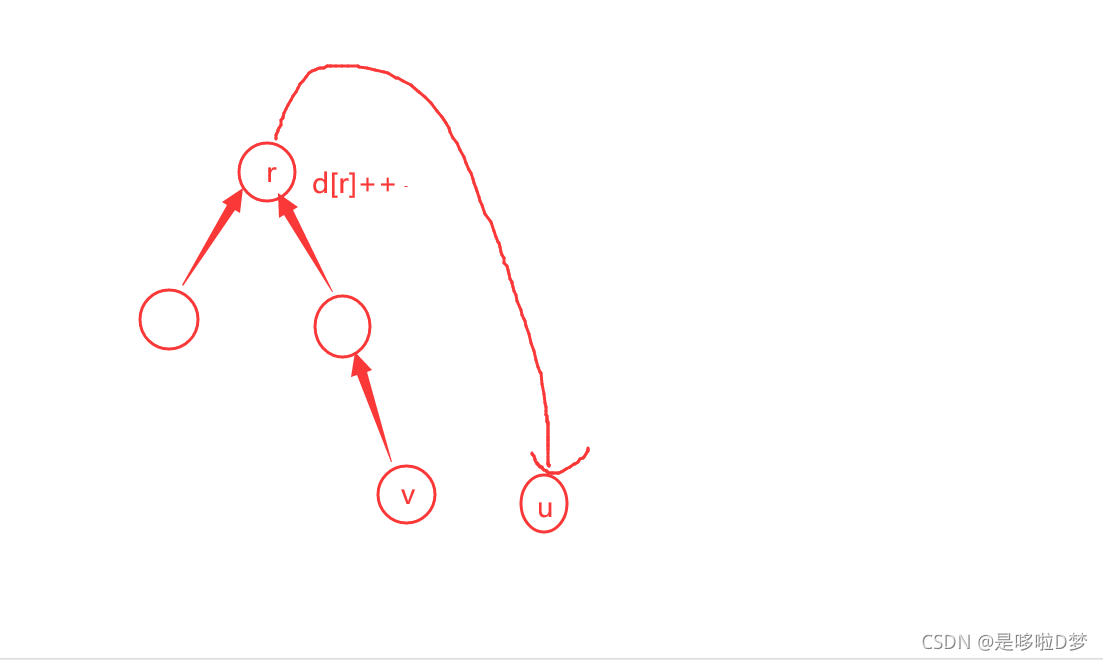
• 如何使整个连通分量的元素值均 + 1，考虑在 v 所属连通分量的根 $r$ 挂一个差分标记，最后从根往下 dfs 即可（显然我们需要边用并查集维护，边构成一棵新树）。由于 u 要与 v 所属连通分量连接，但又要保证 u 的答案不会因为 r 的差分标记使得答案 + 1，可以将 u 作为 v 连通分量的新根，并建图 add(u,r) 即可。如下图
  

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;

struct E{ 
	int u,v,next; 
}e[N*2];
int vex[N],d[N],tot,ans[N],fa[N],a[N];
vector<int>vec[N];

int find(int x){
	if(x==fa[x])return x;
	else return fa[x]=find(fa[x]); 
}
int add(int u,int v){
	tot++;
	e[tot].u=u;
	e[tot].v=v;
	e[tot].next=vex[u];
	vex[u]=tot;
}
void dfs(int u,int fa){
	ans[u]=d[u];
	ans[u]+=ans[fa];
	for(int i=vex[u];i;i=e[i].next){
		int v=e[i].v;
		if(v==fa)continue;
		dfs(v,u);
	}
}
struct node{
	int a,id;
}p[N];
int cmp(node x,node y){
	return x.a<y.a;
}


int main() {
	cin.tie(0);
	cout.tie(0);
	int T,n,u,v;
	cin>>T;
	while(T--){
		cin>>n;
		tot=0;
		for(int i=1;i<=n;i++){
		   vec[i].clear();
		   d[i]=vex[i]=ans[i]=0;
		   fa[i]=i;
		}
		for(int i=1;i<n;i++){
			cin>>u>>v;
			vec[u].push_back(v);
			vec[v].push_back(u); 
		}
		for(int i=1;i<=n;i++){
			cin>>a[i];
			p[i].id=i;
			p[i].a=a[i];
		}
		sort(p+1,p+n+1,cmp);
		for(int i=1;i<=n;i++){
			for(int j=0;j<vec[p[i].id].size();j++){
				int v=vec[p[i].id][j];
				if(a[v]>p[i].a)continue; 
				int x=find(v);
				d[x]++;
				add(x,p[i].id);
				add(p[i].id,x);
				fa[x]=p[i].id;
			}
		}
		int root=find(1);
		dfs(root,0);
		for(int i=1;i<=n;i++)cout<<ans[i]+1<<'\n'; 
	}
	return 0;
}