[数据结构与算法]【LeetCode】回溯算法专题讲解

回溯算法系列

17. 电话号码的字母组合

Difficulty: 中等

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。答案可以按 任意顺序 返回。

给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

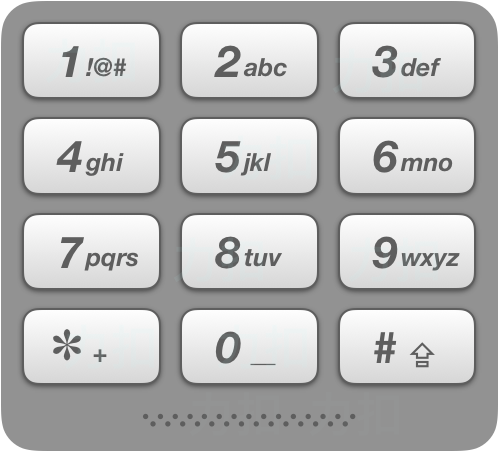
示例 1：

输入：digits = "23"
输出：["ad","ae","af","bd","be","bf","cd","ce","cf"]

示例 2：

输入：digits = ""
输出：[]

示例 3：

输入：digits = "2"
输出：["a","b","c"]

提示：

• 0 <= digits.length <= 4
• digits[i] 是范围 ['2', '9'] 的一个数字。

Solution

Language: javascript

?var letterCombinations = function(digits) {

    if (!digits) return []

    let numMap = {
        2: ['a', 'b', 'c'],
        3: ['d', 'e', 'f'],
        4: ['g', 'h', 'i'],
        5: ['j', 'k', 'l'],
        6: ['m', 'n', 'o'],
        7: ['p', 'q', 'r', 's'],
        8: ['t', 'u', 'v'],
        9: ['w', 'x', 'y', 'z'],
    }

    const result = [];

    function backTrack(digits, index, str) {
        let arr = numMap[digits[index]];
        if(index === digits.length - 1) {
            arr.forEach((str2) => {
                result.push(str + str2);
            })
            return;
        }
        arr.forEach((str2) => {
            backTrack(digits, index + 1, str + str2);
        })
    }

    backTrack(digits, 0, '');
    return result;
};

22. 括号生成

Difficulty: 中等

数字 n 代表生成括号的对数，请你设计一个函数，用于能够生成所有可能的并且 有效的 括号组合。

有效括号组合需满足：左括号必须以正确的顺序闭合。

示例 1：

输入：n = 3
输出：["((()))","(()())","(())()","()(())","()()()"]

示例 2：

输入：n = 1
输出：["()"]

提示：

• 1 <= n <= 8

Solution

Language: javascript

?/**
 * @param {number} n
 * @return {string[]}
 */
var generateParenthesis = function(n) {
    const res = [];
    function helper(cur, l, r) {
        if(l === 0 && r === 0) {
            res.push(cur);
        }
        if(l !== 0) {
            helper(cur + "(", l - 1, r);
        }
        if(r > l) {
            helper(cur + ")", l, r - 1);
        }
    }
    helper("", n, n);
    return res;
};

39. 组合总和

Difficulty: 中等

给定一个无重复元素的正整数数组 candidates 和一个正整数 target ，找出 candidates 中所有可以使数字和为目标数 target 的唯一组合。

candidates 中的数字可以无限制重复被选取。如果至少一个所选数字数量不同，则两种组合是唯一的。

对于给定的输入，保证和为 target 的唯一组合数少于 150 个。

示例 1：

输入: candidates = [2,3,6,7], target = 7
输出: [[7],[2,2,3]]

示例 2：

输入: candidates = [2,3,5], target = 8
输出: [[2,2,2,2],[2,3,3],[3,5]]

示例 3：

输入: candidates = [2], target = 1
输出: []

示例 4：

输入: candidates = [1], target = 1
输出: [[1]]

示例 5：

输入: candidates = [1], target = 2
输出: [[1,1]]

提示：

• 1 <= candidates.length <= 30
• 1 <= candidates[i] <= 200
• candidate 中的每个元素都是独一无二的。
• 1 <= target <= 500

Solution

Language: javascript

?/**
 * @param {number[]} candidates
 * @param {number} target
 * @return {number[][]}
 */
var combinationSum = function(candidates, target) {
    const res = [];
    const helper = (nums, res, target, temp, start) => {
        if(target < 0) return;
        if(target == 0) {
            res.push([...temp]);
            return;
        }
        for(let i = start; i < nums.length; i++) {
            temp.push(nums[i]);
            // 题目给的数组 找到的结果 当前的这一项被target减去的值（传递下去是为了对以后的递归结束做判断） 当前加上当前值的数组（后面是为了给我们target为0的时候push的一个数组，记录的是每一次递归的节点） start（下一个递归的节点开始的位置）
            helper(nums, res, target - nums[i], temp, i);
            temp.pop();
        }
    }
    helper(candidates, res, target, [], 0);
    return res;
};

40. 组合总和 II

Difficulty: 中等

给定一个数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的每个数字在每个组合中只能使用一次。

**注意：**解集不能包含重复的组合。

示例 1:

输入: candidates = [10,1,2,7,6,1,5], target = 8,
输出:
[
[1,1,6],
[1,2,5],
[1,7],
[2,6]
]

示例 2:

输入: candidates = [2,5,2,1,2], target = 5,
输出:
[
[1,2,2],
[5]
]

提示:

• 1 <= candidates.length <= 100
• 1 <= candidates[i] <= 50
• 1 <= target <= 30

Solution

Language: JavaScript

?/**
 * @param {number[]} candidates
 * @param {number} target
 * @return {number[][]}
 */
 var combinationSum2 = function(candidates, target) {
    if(candidates === null || candidates.length === 0) return [];
    const res = [];
    // 排序的作用就是为了去重
    candidates.sort((a, b) => a - b);
    const helper = (res, nums, target, temp, start) => {
        // < 的话 说明不满足 return
        if(target < 0) return;
        // 等于的话就push 要记住push的是拷贝后的 而不是 temp 的指针 因为temp在之后还会改变
        if(target === 0) {
            res.push([...temp]);
            return;
        }

        for(let i = start; i < nums.length; i++) {
            // 当前的不是第一个 且 跟之前的重复了
            if(i !== start && nums[i] === nums[i - 1]) continue;
            temp.push(nums[i]);
            // 保存结果的集合 传入的要使用的数组 跳到下一个节点的时候需要进行target减去当前的值的操作 加上当前的值后的节点路径集合 不能取到当前值（直接快进到下一个start）
            helper(res, nums, target - nums[i], temp, i + 1);
            temp.pop();
        }
    }
    helper(res, candidates, target, [], 0);
    return res;
};

22. 括号生成

Difficulty: 中等

给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

示例 1：

输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

示例 2：

输入：nums = [0,1]
输出：[[0,1],[1,0]]

示例 3：

输入：nums = [1]
输出：[[1]]

提示：

• 1 <= nums.length <= 6
• -10 <= nums[i] <= 10
• nums 中的所有整数 互不相同

Solution

Language: javascript

?/**
 * @param {number[]} nums
 * @return {number[][]}
 */
var permute = function(nums) {
    const res = [];
    function backTrack(temp) {
        if(temp.length === nums.length) {
            res.push([...temp]);
            return;
        }
        for(let i = 0; i < nums.length; i++) {
            if(temp.indexOf(nums[i]) !== -1 ) continue;
            temp.push(nums[i]);
            backTrack(temp, i + 1);
            temp.pop();
        }
    }
    backTrack([]);
    return res;
};

47. 全排列 II

Difficulty: 中等

给定一个可包含重复数字的序列 nums ，按任意顺序 返回所有不重复的全排列。

示例 1：

输入：nums = [1,1,2]
输出：
[[1,1,2],
 [1,2,1],
 [2,1,1]]

示例 2：

输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

提示：

• 1 <= nums.length <= 8
• -10 <= nums[i] <= 10

Solution

Language: javascript

?/**
 * @param {number[]} nums
 * @return {number[][]}
 */
var permuteUnique = function(nums) {
    const traverse = (res, cur, nums, used) => {
        if(cur.length === nums.length) {
            res.push([...cur]);
        } else {
            for(let i = 0; i < nums.length; i++) {
                // 当前值被使用了
                if(used[i]) {
                    continue;
                }
                // 当前值和之前的值是一样的 但是没关系 我们还是能够考虑这一项的
                // 因为没说值是不重复的 只说的是 item 出现的次数不能超过 1
                if(i > 0 && nums[i] === nums[i - 1]) {
                    // 如果之前的那一项还在使用，就说明是在之前的那一项的流程里面
                    // 所以能够考虑这一项
                    // 如果之前的那一项没在使用了，就说明之前那一项已经走完了，
                    // 所有的结果全都考虑到了，所以就没必要再考虑这一项了
                    if(!used[i - 1]) {
                        continue;
                    }
                }
                cur.push(nums[i]);
                used[i] = true; // 使用过了
                traverse(res, cur, nums, used);
                used[i] = false; // 不使用了
                cur.pop();
            }
        }
    }
    nums.sort((a, b) => a - b);
    const res = [];
    traverse(res, [], nums, new Array(nums.length).fill(false));
    return res;
};

50. Pow(x, n)

Difficulty: 中等

实现 ，即计算 x 的 n 次幂函数（即，xⁿ）。

示例 1：

输入：x = 2.00000, n = 10
输出：1024.00000

示例 2：

输入：x = 2.10000, n = 3
输出：9.26100

示例 3：

输入：x = 2.00000, n = -2
输出：0.25000
解释：2-2 = 1/22 = 1/4 = 0.25

提示：

• -100.0 < x < 100.0
• -2<sup>31</sup> <= n <= 2<sup>31</sup>-1
• -10<sup>4</sup> <= x<sup>n</sup> <= 10<sup>4</sup>

Solution

Language: javascript

?/**
 * @param {number} x
 * @param {number} n
 * @return {number}
 */
var myPow = function(x, n) {
    if(n < 0) {
        x = 1 / x;
        n = -n;
    }
    const fastPow = (x, n) => {
        if(n === 0) {
            return 1;
        }
        let half = fastPow(x, parseInt(n / 2));
        return n % 2 === 0 ? half * half : half * half * x;
    }
    return fastPow(x, n);
};

51. N 皇后

Difficulty: ** 每一种解法包含一个不同的 n 皇后问题 的棋子放置方案，该方案中 ‘Q’ 和 ‘.’ 分别代表了皇后和空位。 示例 1： 输入：n = 4 输出：[[".Q…","…Q",“Q…”,"…Q."],["…Q.",“Q…”,"…Q",".Q…"]] 解释：如上图所示，4 皇后问题存在两个不同的解法。 示例 2： 输入：n = 1 输出：[[“Q”]] 提示： 1 <= n <= 9 皇后彼此不能相互攻击，也就是说：任何两个皇后都不能处于同一条横行、纵行或斜线上。 **

n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回所有不同的 n 皇后问题 的解决方案。

每一种解法包含一个不同的 n 皇后问题 的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位。

示例 1：

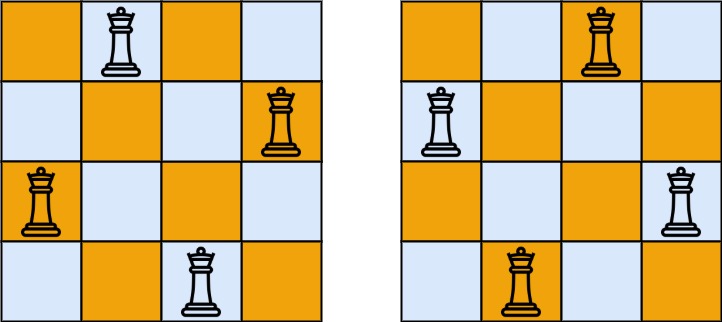
输入：n = 4
输出：[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
解释：如上图所示，4 皇后问题存在两个不同的解法。

示例 2：

输入：n = 1
输出：[["Q"]]

提示：

• 1 <= n <= 9
• 皇后彼此不能相互攻击，也就是说：任何两个皇后都不能处于同一条横行、纵行或斜线上。

Solution

Language: JavaScript

?/**
 * @param {number} n
 * @return {string[][]}
 */
var solveNQueens = function(n) {
    function isValid(row, col, chessBoard, n) {

        for(let i = 0; i < row; i++) {
            if(chessBoard[i][col] === 'Q') {
                return false
            }
        }

        for(let i = row - 1, j = col - 1; i >= 0 && j >= 0; i--, j--) {
            if(chessBoard[i][j] === 'Q') {
                return false
            }
        }

        for(let i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++) {
            if(chessBoard[i][j] === 'Q') {
                return false
            }
        }
        return true
    }

    function transformChessBoard(chessBoard) {
        let chessBoardBack = []
        chessBoard.forEach(row => {
            let rowStr = ''
            row.forEach(value => {
                rowStr += value
            })
            chessBoardBack.push(rowStr)
        })

        return chessBoardBack
    }

    let result = []
    function backtracing(row,chessBoard) {
        if(row === n) {
            result.push(transformChessBoard(chessBoard))
            return
        }
        for(let col = 0; col < n; col++) {
            if(isValid(row, col, chessBoard, n)) {
                chessBoard[row][col] = 'Q'
                backtracing(row + 1,chessBoard)
                chessBoard[row][col] = '.'
            }
        }
    }
    let chessBoard = new Array(n).fill([]).map(() => new Array(n).fill('.'))
    backtracing(0,chessBoard)
    return result

};

78. 子集

Difficulty: 中等

给你一个整数数组 nums ，数组中的元素 互不相同 。返回该数组所有可能的子集（幂集）。

解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。

示例 1：

输入：nums = [1,2,3]
输出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

示例 2：

输入：nums = [0]
输出：[[],[0]]

提示：

• 1 <= nums.length <= 10
• -10 <= nums[i] <= 10
• nums 中的所有元素 互不相同

Solution

Language: JavaScript

?/**
 * @param {number[]} nums
 * @return {number[][]}
 */
 var subsets = function(nums) {
    const res = [];
    if(nums === null) return res;
    const dfs = (res, nums, list, start) => {
        res.push([...list]);
        for(let i = start; i < nums.length; i++) {
            list.push(nums[i]);
            dfs(res, nums, list, i + 1);
            list.pop();
        }
    }
    dfs(res, nums, [], 0);
    return res;
};

90. 子集 II

Difficulty: ** 示例 1： 输入：nums = [1,2,2] 输出：[[],[1],[1,2],[1,2,2],[2],[2,2]] 示例 2： 输入：nums = [0] 输出：[[],[0]] 提示： 1 <= nums.length <= 10 -10 <= nums[i] <= 10 **

给你一个整数数组 nums ，其中可能包含重复元素，请你返回该数组所有可能的子集（幂集）。

解集 不能 包含重复的子集。返回的解集中，子集可以按 任意顺序 排列。

示例 1：

输入：nums = [1,2,2]
输出：[[],[1],[1,2],[1,2,2],[2],[2,2]]

示例 2：

输入：nums = [0]
输出：[[],[0]]

提示：

• 1 <= nums.length <= 10
• -10 <= nums[i] <= 10

Solution

Language: javascript

?/**
 * @param {number[]} nums
 * @return {number[][]}
 */
 var subsetsWithDup = function(nums) {
    const res = [];
    nums.sort((a, b) => a - b);
    function backTrack(nums, res, list, start) {
        res.push([...list]);
        for(let i = start; i < nums.length; i++) {
            if(i > start && nums[i] === nums[i - 1]) continue;
            list.push(nums[i]);
            backTrack(nums, res, list, i + 1);
            list.pop();
        }
    }
    backTrack(nums, res, [], 0);
    return res;
};

140. 单词拆分 II

Difficulty: 困难

给定一个非空字符串 s 和一个包含非空单词列表的字典 wordDict，在字符串中增加空格来构建一个句子，使得句子中所有的单词都在词典中。返回所有这些可能的句子。

说明：

• 分隔时可以重复使用字典中的单词。
• 你可以假设字典中没有重复的单词。

示例 1：

输入:
s = "catsanddog"
wordDict = ["cat", "cats", "and", "sand", "dog"]
输出:
[
  "cats and dog",
  "cat sand dog"
]

示例 2：

输入:
s = "pineapplepenapple"
wordDict = ["apple", "pen", "applepen", "pine", "pineapple"]
输出:
[
  "pine apple pen apple",
  "pineapple pen apple",
  "pine applepen apple"
]
解释: 注意你可以重复使用字典中的单词。

示例 3：

输入:
s = "catsandog"
wordDict = ["cats", "dog", "sand", "and", "cat"]
输出:
[]

Solution

Language: javascript

BT + temp 的解法

?/**
 * @param {string} s
 * @param {string[]} wordDict
 * @return {string[]}
 */
var wordBreak = function(s, wordDict) {
    const res = [];
    function backTrack(temp, start) {
        if(start === s.length) {
            res.push(temp.join(" "));
            return;
        }
        for(let i = start + 1; i <= s.length; i++) {
            let str = s.substring(start, i);
            if(wordDict.indexOf(str) === -1) continue;
            temp.push(str);
            // 上面的 i 是左闭右开的，我们当前取不到 i，那下一次就是 i
            backTrack(temp, i);
            temp.pop();
        }
    }
    backTrack([], 0);
    return res;
};

BT + DFS 的解法

/**
 * @param {string} s
 * @param {string[]} wordDict
 * @return {string[]}
 */
var wordBreak = function (s, wordDict) {
  function backTrack(s, wordDict, start) {
    const res = [];
    for (let i = start + 1; i <= s.length; i++) {
      //如果拆解的子串不存在于字典中，就继续拆
      let str = s.substring(start, i);
      if (wordDict.indexOf(str) === -1) {
        continue;
      }
      //走到下面这个地方，说明拆分的子串str存在于字典中
      //如果正好拆完了，我们直接把最后一个子串添加到res中返回
      if (i === s.length) {
        res.push(str);
      } else {
        //如果没有拆完，我们对剩下的子串继续拆分
        //然后用当前的子串str和剩下的子串进行拼接（注意如果剩下的子串不能
        //完全拆分，remainRes就会为空，就不会进行拼接）
        const remainRes = backTrack(s, wordDict, i);
        for (let remainStr of remainRes) {
          res.push(str + " " + remainStr);
        }
      }
    }
    return res;
  }
  return backTrack(s, wordDict, 0);
};

216. 组合总和 III

Difficulty: 中等

找出所有相加之和为 n 的 **k 个数的组合。**组合中只允许含有 1 - 9 的正整数，并且每种组合中不存在重复的数字。

说明：

• 所有数字都是正整数。
• 解集不能包含重复的组合。

示例 1:

输入: k = 3, n = 7
输出: [[1,2,4]]

示例 2:

输入: k = 3, n = 9
输出: [[1,2,6], [1,3,5], [2,3,4]]

Solution

Language: JavaScript

?/**
 * @param {number} k
 * @param {number} n
 * @return {number[][]}
 */
var combinationSum3 = function(k, n) {
    const res = [];
    function dfs(res, temp, k, start, n) {
        // 满足一个就没有意义了
        if(temp.length === k || n <= 0) {
            // 找到符合标准的
            if(temp.length === k && n === 0) {
                res.push([...temp]);
            }
            return;
        }
        // 从 1 到 9 开始尝试
        for(let i = start; i <= 9; i++) {
            // 尝试当前的一项
            temp.push(i);
            // 进行下一步的尝试，并且把当前的 n 进行更新
            dfs(res, temp, k, i + 1, n - i);
            // 撤回当前的尝试 进行下一个尝试
            temp.pop();
        }
    }
    dfs(res, [], k, 1, n);
    return res;
};