[数据结构与算法]回溯-二叉树的最近公共祖先，从上往下判断or记录路径

剑指 Offer 64. 求1+2+…+n

求 1+2+…+n ，要求不能使用乘除法、for、while、if、else、switch、case等关键字及条件判断语句（A?B:C）。

碰到这种，由于头脑不好使，直接看题解。

函数需要的功能：

1. 实现 “当 n = 1n=1 时终止递归” 的需求，可通过短路效应实现。

class Solution:
    def __init__(self):
        self.res = 0
    def sumNums(self, n: int) -> int:
        n > 1 and self.sumNums(n - 1) #只要n>1 就会递归 n-1
        self.res += n
        return self.res

剑指 Offer 68 - I. 二叉搜索树的最近公共祖先

给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

得记录寻找路径。
通过输出路径可以验证自己是否错误，从两个列表后面开始读，第一个出现就是公共祖先。我这里直接忽略二叉搜索树的条件，就是一般方法。

看结果，记录路径效率有点低，先献上

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
        def findpath(root, target):
            if not root: return
            tmp.append(root)
            if root == target:
                self.path.append(list(tmp)) # 坑过 要加list
                self.find = True
                # 不能return，因为要回溯，减去路径记录
            # tmp.append(root) # 如果是target，放这里会忘记加到tmp
            if not self.find: # 减枝
                findpath(root.left, target)
                findpath(root.right, target)
            tmp.pop()
        
        self.path = []
        tmp = []
        self.find = False
        findpath(root, p)
        self.find = False
        findpath(root, q)
        a, b = self.path[0], self.path[1]
        index = min(len(a), len(b)) - 1
        # 调bugger
        x = [e.val for e in a]
        y = [e.val for e in b]
        print(x)
        print(y)
        while index >= 0:
            if a[index] == b[index]:
                return a[index]
            index -= 1 # index忘记减一了，所以一直死循环超时
        return None

官方解题

因为已知是二叉搜索树，那就要用该条件。
说明:
所有节点的值都是唯一的。
p、q 为不同节点且均存在于给定的二叉搜索树中。
思想：
从上往下找

class Solution:
    def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
        while root:
            if root.val < p.val and root.val < q.val: # p,q 都在 root 的右子树中
                root = root.right # 遍历至右子节点
            elif root.val > p.val and root.val > q.val: # p,q 都在 root 的左子树中
                root = root.left # 遍历至左子节点
            else: break # 这里包括任意一点等于root, 分别在左右子树
        return root

剑指 Offer 68 - II. 二叉树的最近公共祖先

这里没有二叉搜索树的特征，
说明:
所有节点的值都是唯一的。
p、q 为不同节点且均存在于给定的二叉树中。

考虑通过递归对二叉树进行先序遍历，当遇到节点 p 或 q 时返回。从底至顶回溯，当节点 p,q 在节点 root 的异侧时，节点 root 即为最近公共祖先，则向上返回 rootroot 。

每个节点都会往上一层传值，最终传到根节点。

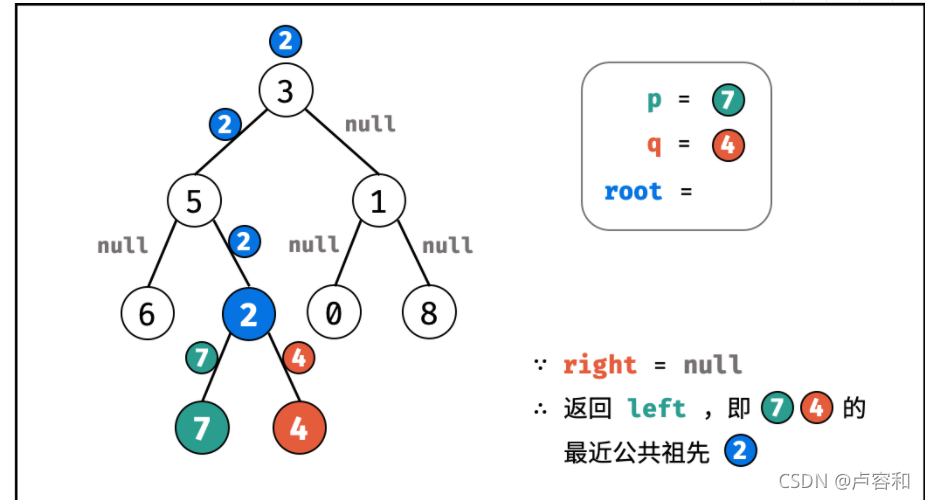
个人理解上面图：

1. 遇到目标节点p/q，就会往上层传。
2. 当某一节点不知道穿右子树还是左子树，传有值的（代表目标节点），除非两个值都为None，就传None。
3. 最只要的一点还是，当两边都有值就可以判断该节点为公共祖先，最后就一直往上传。
4. 还有一种结果，最终的节点为目标节点的其中之一，因为此时P可能是Q的祖先，遇到P之后就停止往下搜索了。

class Solution:
    def lowestCommonAncestor(self, root: TreeNode, p: TreeNode, q: TreeNode) -> TreeNode:
        if not root or root == p or root == q: return root # 如果root为p，包含q为其子节点，不需在往下遍历
        left = self.lowestCommonAncestor(root.left, p, q)
        right = self.lowestCommonAncestor(root.right, p, q)
        if not left and not right: return None # 1.
        if not left: return right # 3.
        if not right: return left # 4.
        return root # 2. if left and right: