7-2 最小生成树-kruskal (40 分)

文章目录

- 7-2 最小生成树-kruskal (40 分)
前言
一、题
- 1.最小生成树-kruskal
- 2.注意点
二、解

前言

克鲁斯卡尔（Kruskal）算法其基本思想是：假设连通网G=（V，E），令最小生成树的初始状态为只有n个顶点而无边的非连通图T=（V，{}），概述图中每个顶点自成一个连通分量。在E中选择代价最小的边，若该边依附的顶点分别在T中不同的连通分量上，则将此边加入到T中；否则，舍去此边而选择下一条代价最小的边。依此类推，直至T中所有顶点构成一个连通分量为止。

一、题

1.最小生成树-kruskal

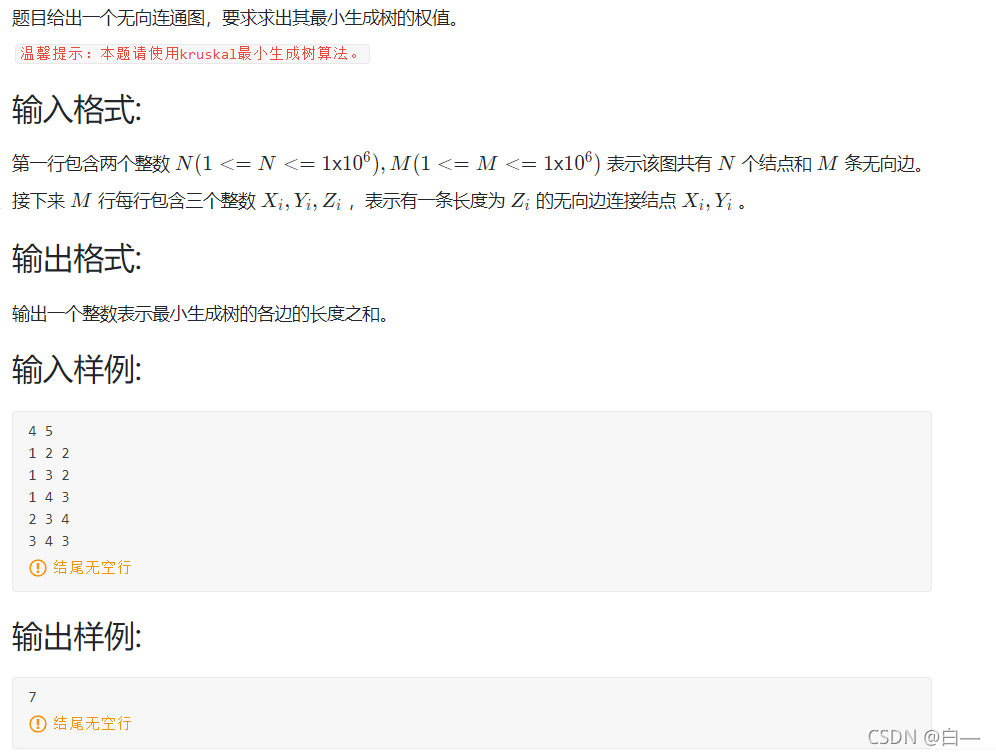
在这里插入图片描述

2.注意点

注意点：用c写，并使用数组存储时，因为数组太长，出现运行超时的情况，如下
在这里插入图片描述
所以如要使用数组写，使用c++即可

二、解

1.过程

过程如下：
1.将每个点当作一棵树，所有点组成森林
2.给每条边排序，小的在前，大的在后，方便使用
3.每次找最小的边，先判断这条边的两个点是否在同一颗树中，若在，则判断下一条边；若不在，将该点与另一个点相连，即改变他的父节点。将每次成功时的边的长度加起来，得到的便是结果。

2.代码

c++代码如下:

#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
struct Edge
{
    int x,y,z;
}a[1000010]; //存储x,y,z的信息
bool cmp(const Edge &a,const Edge &b)//比较大小
{
        return a.z<b.z;
}
int n,m;
int tree[1000010];//建造森林,初始时每个点就是一棵树
int findfather(int x)
{
    if(tree[x]!=x)
        return tree[x]=findfather(tree[x]);  //并查集,更新父节点,减少了一些多于查找,使得查询速度更快
    return tree[x];
}
int kruskal(struct Edge a[],int N,int M)
{
    sort(a,a+m,cmp);//先将给定的数据进行排序,边短的排在前面，长的在后。
    for(int i=1; i<=N; i++)
        tree[i]=i;//每棵树的父节点是自己
    int sum=0;
    for(int i=0; i<M; i++)
    {
        int x=a[i].x;
        int y=a[i].y;
        int z=a[i].z;
        if(findfather(x)!=findfather(y))//判断两个是否在同一颗树中,不在同一棵树时才将该树加入
        {
            tree[findfather(x)]=findfather(y);//加入树
            sum+=z;//计算长度
        }
    }
    return sum;
}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=0;i<m;i++)
        scanf("%d%d%d",&a[i].x,&a[i].y,&a[i].z);
    printf("%d",kruskal(a,n,m));
    return 0;
}