常见的背包问题:0/1背包,完全背包,多重背包。?
背包问题大意:将一些标有容量和价值的物品装入一个有着固定容量的背包,求背包中能存放物品的最大价值和。
- 背包容量:total。
- 物品数量:n。
- 第i件物品重量:w[i]。
- 第i件物品价值:v[i]。
- 多重背包时与第i件物品相同的个数s[i]。
处理思路:二维dp转一维dp,打表处理。
0/1背包:
将一些物品往背包放时,每样物品只有一件,不能多次存放。在做某一轮(某一物品)处理时,需要考虑上一轮时拥有的情况,需要在上一轮基础减去w[i],相当于为下一件物品所腾出了 w[i] 的空间。
即二维dp:dp[i][j] = max(dp[i - 1][j] , dp[i - 1][j - w[i]] + v[i])
优化为一维滚动dp:dp[j] = max(dp[j] , dp[j - w[i]] + v[i])
二维dp核心代码:
int [][]dp = new int [n + 1][total + 1];//空出最左列和最上列
for(int i = 1; i <= n;i++) {//物品属性数组索引从1开始
for(int j = 1;j <= total;j++) {
if(j < w[i]) {//当前容量不及物品容量时
dp[i][j] = dp[i - 1][j];
}else {
dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - w[i]] + v[i]);
}
}
}一维滚动dp核心代码:
int []dp = new int [total + 1];
for(int i = 0; i < n;i++) {//物品属性数组索引从0开始
for(int j = total;j >= w[i];j--) {//内层循环需要从后往前遍历,防止得到前面的解时将上一轮解覆盖,导致后面解出错。
dp[j] = Math.max(dp[j], dp[j - w[i]] + v[i]);
}
}完全背包:
将一些物品往背包放时,每样物品不限件数,可以多次存放。在做某一轮(某一物品)处理时,需要考虑本轮拥有的情况,在本轮的基础减去w[i],相当于对某些物品不限件数时的累加。
即二维dp:dp[i][j] = max(dp[i][j] , dp[i][j - w[i]] + v[i])
优化为一维滚动dp:dp[j] = max(dp[j] , dp[j - w[i]] + v[i])
注意 0/1?背包和完全背包的一维滚动数组dp的状态方程都一样,但其含义不同。通俗的说,0/1背包利用的是上一轮的部分解。而完全背包利用的是次轮的部分解。
二维dp核心代码:
int [][]dp = new int [n + 1][total + 1];//开始空出最左列和最上列
for(int i = 1; i <= n;i++) {
for(int j = 1;j <= total;j++) {//物品属性数组索引从1开始
if(j < w[i]) {//当前容量不及物品容量时
dp[i][j] = dp[i - 1][j];
}else {
dp[i][j] = Math.max(dp[i][j], dp[i][j - w[i]] + v[i]);
}
}
}一维滚动dp核心代码:
int []dp = new int [total + 1];
for(int i = 0; i < n;i++) {//物品属性数组索引从0开始
for(int j = w[i];j <= total;j++) {//内层循环正向遍历,后面解需要利用前面解,“物品的叠加”
dp[j] = Math.max(dp[j], dp[j - w[i]] + v[i]);
}
}多重背包:
将一些物品往背包放时,每样物品有固定的件数,相当于在0/1背包的基础上增加了一些相同物品,但同时相同物品的个数又不是无限的。
可以在0/1背包的一维滚动dp的基础上稍作修改:dp[j] = max(dp[j] , dp[j - k * w[i]] + k * v[i])。
一维滚动dp核心代码:O(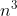 )
)
int []dp = new int [total + 1];
for(int i = 0; i < n;i++) {//物品属性数组索引从0开始
for(int j = total;j >= 1;j--) {
for(int k = 0;k <= s[i] && k*w[i] <= j;k++){//物品件数既不能超出给定的数量,也不能总容量大于当前背包容量j
dp[j] = Math.max(dp[j], dp[j - k * w[i]] + k * v[i]);
}
}
}注:复杂度太大,需用二进制优化。