1 模型
带时间窗的车辆路径问题是典型的NP难题,一种常用的求解方法是先对顾客分组,后进行路径优化的两阶段启发式算法.传统算法在顾客分组时主要考虑顾客的空间位置关系,但是忽略了顾客对服务时间窗口的要求.本文同时考虑顾客的时间和空间特性,提出了一种基于时空度量的顾客分组方法.在路径优化阶段,本文提出了一种禁忌搜索算法来进行求解,该算法中禁忌的对象不是解,而是这些解的目标函数值的区间,以便于提高收敛效率.作为验证,本文以Solomon标杆问题集为算例进行演算,结果表明,在窄时间窗约束下,基于时空距离的两阶段启发式算法明显优于基于空间距离的算法,且部分算例的解达到了国内外已发表的最好解.








2 部分代码
clear
clc
%% 用importdata这个函数来读取文件
tic
rc207=importdata('rc207.txt');
cap=1000; ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?%车辆负荷
E=rc207(1,5); ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?%仓库时间窗开始时间
L=rc207(1,6); ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?%仓库时间窗结束时间
vertexs=rc207(:,2:3); ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?%所有点的坐标x和y
customer=vertexs(2:end,:); ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?%顾客坐标
cusnum=size(customer,1); ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?%顾客数
vecnum=cusnum; ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?%车辆数
demands=rc207(2:end,4); ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?%需求量
a=rc207(2:end,5); ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?%顾客时间窗开始时间[a[i],b[i]]
b=rc207(2:end,6); ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?%顾客时间窗结束时间[a[i],b[i]]
s=rc207(2:end,7); ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?%客户点的服务时间
h=pdist(vertexs);
dist=squareform(h); ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ??%距离矩阵,满足三角关系,暂用距离表示花费c[i][j]=dist[i][j]
vehicles_customer=cell(vecnum,1); ? ? ? ? ? ? ? ? ? ? ? ? ??%每辆车所经过的顾客
%% 设置参数
alpha=1;
belta=1;
lamda=0.015;
delta=0.5;
maxIter=1500; ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?%最大迭代次数
%% 初始路径
%% CW法构造VRPTW初始解
%输出init_vc ? ? 每辆车所经过的顾客
%输出init_TD ? ? 所有车行驶的总距离
%输出init_vl ? ? 每辆车的装载量
%输出violate_INTW 判断是否违背时间窗约束,0代表不违背,1代表违背
% [init_vc,init_TD] = init_TW(rc207,L,demands,a,b,s,dist,cap);
[init_vc] =?init(cusnum,a,demands,cap);
S=init_vc;
Sbest=S; ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?%全局最优解
[f]=costFuction(S,a,b,s,L,dist,demands,cap,alpha,belta); ? ? ? ? ? ?% 计算初始解的成本
fBest=f;
%% Tabu Search
TbList=zeros(cusnum,cusnum); ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?%禁忌表
TbLength=20; ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?%禁忌长度
NS=neighborhood(S,cusnum,a,b,s,L,dist,demands,cap,alpha,belta,lamda); ? ??%S的邻域
[subNS]=subNeighbor(TbList,NS,fBest); ? ? ? ? ? ? ? ? ? ? ? ? ? ? ??% non-tabu or allowed by aspiration
iter=0;
while?iter<maxIter
? ?if?~isempty(subNS)
? ? ? [minValue,minIndex]=min(subNS(:,5)); ? ? ? ? ??%从邻域中找出车辆总行驶距离最小的行序号
? ? ? ?value=subNS(minIndex,:); ? ? ? ? ? ? ? ? ? ? ??%提取最小行序号的这一行数组
? ? ? ?i=value(1);
? ? ? ?j=value(2);
? ? ? ?k=value(3);
? ? ? ?p=value(4);
? ? ? ?fS=value(5);
? ? ? ?cS=travel_distance(S,dist);
? ? ? [S_copy]=insert(S,i,j,k,p);
? ? ? ?S_copy=deal_vehicles_customer(S_copy);
? ? ? ?if?fS<fBest
? ? ? ? ? ?fBest=fS;
? ? ? ? ? ?Sbest=deal_vehicles_customer(S_copy);
? ? ? ? ? [feasBest]=decide_Feasible(Sbest,a,b,s,L,dist,demands,cap);
? ? ? ? ? ?S=deal_vehicles_customer(S_copy);?
? ? ? ? ? ?NS=neighborhood(S_copy,cusnum,a,b,s,L,dist,demands,cap,alpha,belta,lamda);
? ? ? ? ? [subNS]=subNeighbor(TbList,NS,fBest);
? ? ? ? ? ?%更新禁忌表
? ? ? ? ? ?for?l=1:cusnum
? ? ? ? ? ? ? ?for?h=1:cusnum
? ? ? ? ? ? ? ? ? ?if?TbList(l,h)~=0
? ? ? ? ? ? ? ? ? ? ? ?TbList(l,h)=TbList(l,h)-1;
? ? ? ? ? ? ? ? ? ?end
? ? ? ? ? ? ? ?end
? ? ? ? ? ?end
? ? ? ? ? ?if?TbList(i,j)==0
? ? ? ? ? ? ? ?TbList(i,j)=TbLength;
? ? ? ? ? ?else
? ? ? ? ? ? ? ?TbList(i,j)=0;
? ? ? ? ? ?end
? ? ? ? ? ?
? ? ? ?else?
? ? ? ? ? ?if?TbList(i,j)==0
? ? ? ? ? ? ? ?S=S_copy;
? ? ? ? ? ? ? ?q=violateLoad(S,demands,cap);
? ? ? ? ? ? ? ?w=violateTW(S,a,b,s,L,dist);
? ? ? ? ? ? ? ?
? ? ? ? ? ? ? ?if?q>0
? ? ? ? ? ? ? ? ? ?alpha=alpha*(1+delta);
? ? ? ? ? ? ? ?end
? ? ? ? ? ? ? ?
? ? ? ? ? ? ? ?if?w>0
? ? ? ? ? ? ? ? ? ?belta=belta*(1+delta);
? ? ? ? ? ? ? ?end
? ? ? ? ? ? ? ?
? ? ? ? ? ? ? ?NS=neighborhood(S,cusnum,a,b,s,L,dist,demands,cap,alpha,belta,lamda);
? ? ? ? ? ? ? [subNS]=subNeighbor(TbList,NS,fBest);
? ? ? ? ? ? ? ?% 更新禁忌表
? ? ? ? ? ? ? ?for?l=1:cusnum
? ? ? ? ? ? ? ? ? ?for?h=1:cusnum
? ? ? ? ? ? ? ? ? ? ? ?if?TbList(l,h)~=0
? ? ? ? ? ? ? ? ? ? ? ? ? ?TbList(l,h)=TbList(l,h)-1;
? ? ? ? ? ? ? ? ? ? ? ?end
? ? ? ? ? ? ? ? ? ?end
? ? ? ? ? ? ? ?end
? ? ? ? ? ? ? ?TbList(i,j)=TbLength;?
? ? ? ? ? ?end
? ? ? ?end
? ?else
? ? ? ?break
? ?end
? ?iter=iter+1;
end
%% 判断当前解是否存在元素丢失情况以及是否存在违反约束的情况
DEL=Judge_Del(Sbest);
[feasible]=decide_Feasible(Sbest,a,b,s,L,dist,demands,cap); ? ?%feasible=0 表示不满足,feasible=1表示满足
bestNV=size(Sbest,1);
bestTD=travel_distance(Sbest,dist);
%% 打印全局最优解路线图
draw_Best(Sbest,vertexs);
toc
3 仿真结果
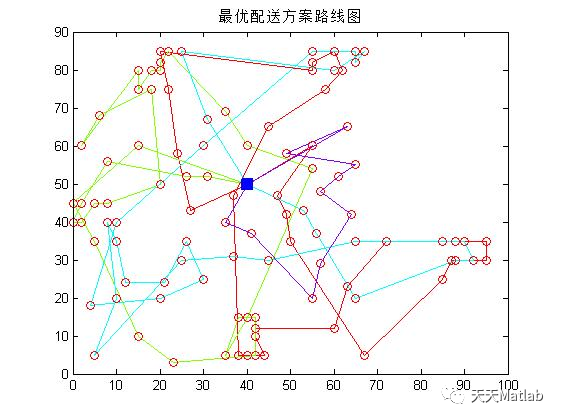
4 参考文献
[1]戚铭尧, 丁国祥, 周游,等. 一种基于时空距离的带时间窗车辆路径问题算法[J]. 交通运输系统工程与信息, 2011(01):89-93.
