[数据结构与算法]二叉树相关面试题【数据结构】

基础面试题

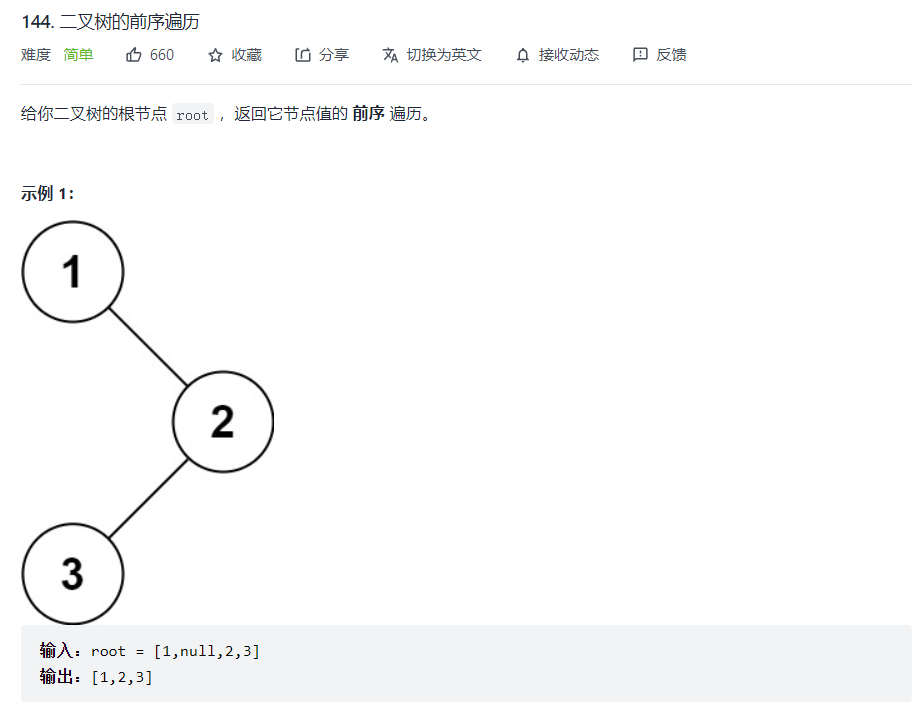
二叉树的前序遍历

题目：在线OJ

思考：

首先，我们要了解，前序遍历就是按照顺序：根节点—左子树—右子树的方式遍历树(根左右)
在访问左右子树的时候，按照上述同样的方法遍历，因此我们可以考虑使用递归来解决

• 创建一个 List，将根节点的元素加入到 List 中
• 递归遍历左子树，把左子树的遍历结果加入到 List 中
• 递归遍历右子树，把右子树的遍历结果加入到 List 中
• 最后返回这个 List 即可

画图分析：

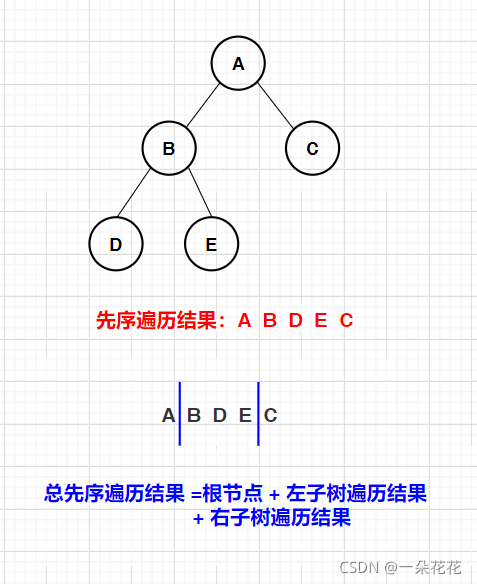
代码实现：

public List<Integer> preorderTraversal(TreeNode root) {
    //创建一个 List
    List<Integer> result = new ArrayList<>();
    if(root == null){
        //空树返回 一个空 List(元素个数为空，但不是null)
        return result;
    }
    //访问根节点
    //把元素 add 到 List中
    result.add(root.val);

    //递归遍历左子树,把左子树的遍历结果加入到List中
    result.addAll(preorderTraversal(root.left));
    //递归遍历右子树,把右子树的遍历结果加入到List中
    result.addAll(preorderTraversal(root.right));

    return result;
}

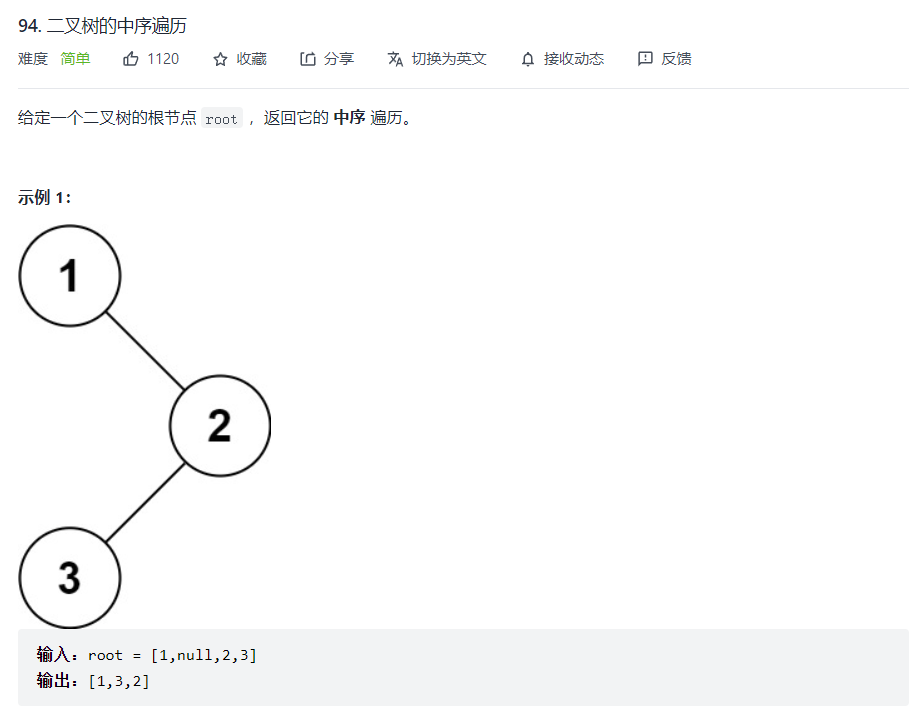
二叉树的中序遍历

题目：在线OJ

思考：

中序遍历是按照顺序：左子树遍历—根节点—右子树遍历的方式来遍历树(左根右)
同先序遍历一样，使用递归解决

画图分析：

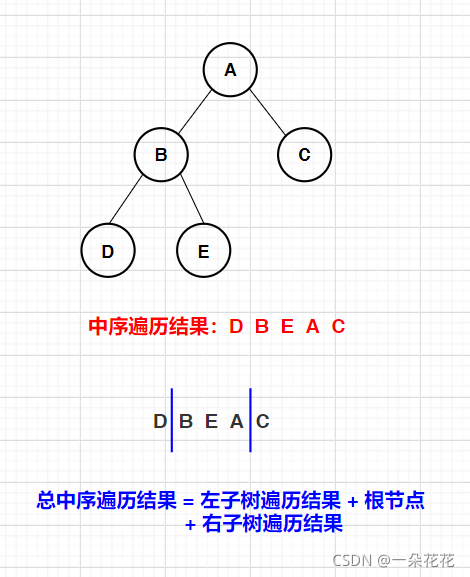
代码实现：

public List<Integer> inorderTraversal(TreeNode root) {
    //创建一个List
    List<Integer> result = new ArrayList<>();
    //空树判断
    if(root == null){
        return result;
    }
    //递归遍历左子树
    result.addAll(inorderTraversal(root.left));
    //根节点
    result.add(root.val);
    //递归遍历右子树
    result.addAll(inorderTraversal(root.right));

    return result;
}

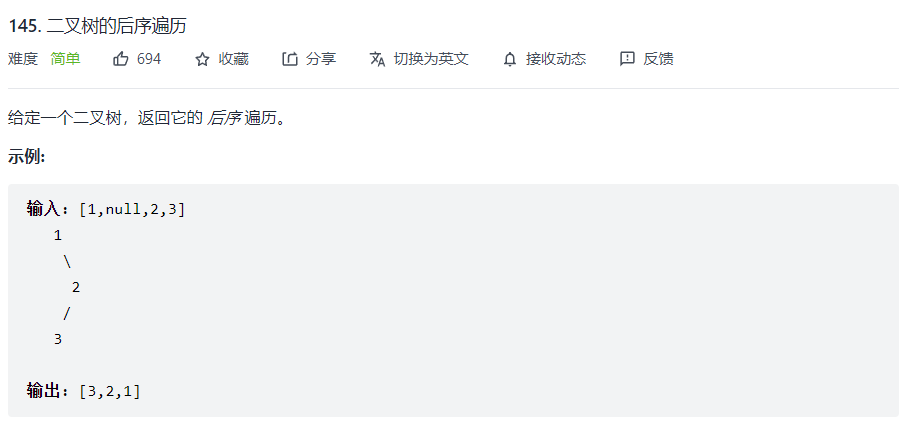
二叉树的后续遍历结果

题目：在线OJ

思考：

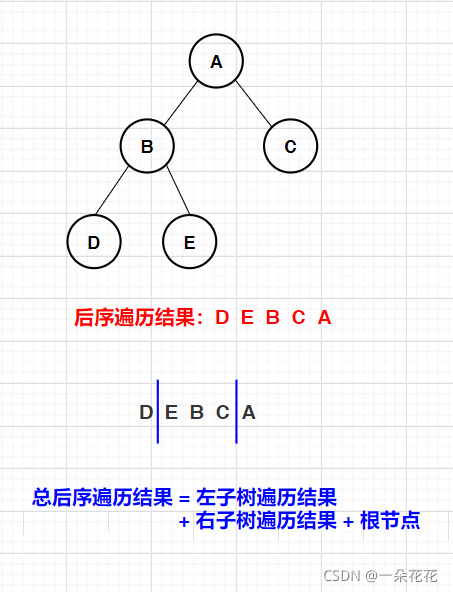
后续遍历按照顺序：左子树遍历—右子树遍历—根节点的遍历方式来遍历树的(左右根)
实现过程参考前序遍历

代码实现：

public List<Integer> postorderTraversal(TreeNode root) {
    //创建一个List
    List<Integer> result = new ArrayList<>();
    //空树判断
    if(root == null){
        return result;
    }
    //左子树遍历
    result.addAll(postorderTraversal(root.left));
    //右子树遍历
    result.addAll(postorderTraversal(root.right));
    //根节点
    result.add(root.val);
    
    return result;
}

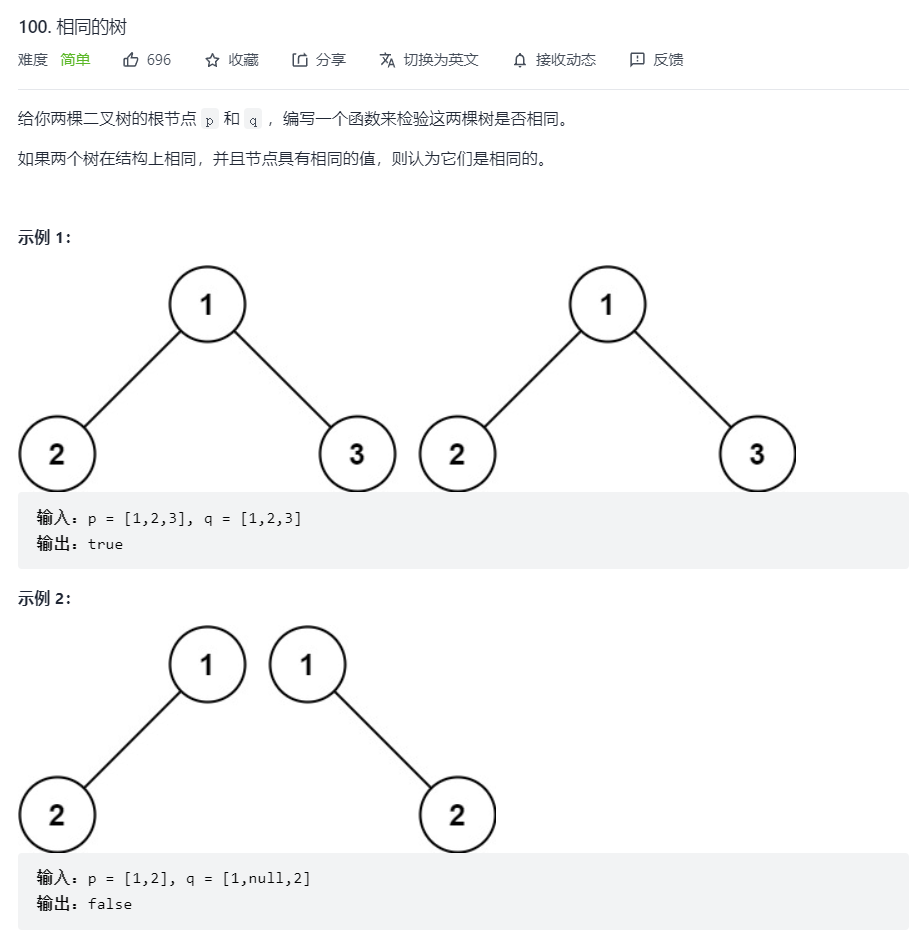
相同的树

题目：在线OJ

思考：

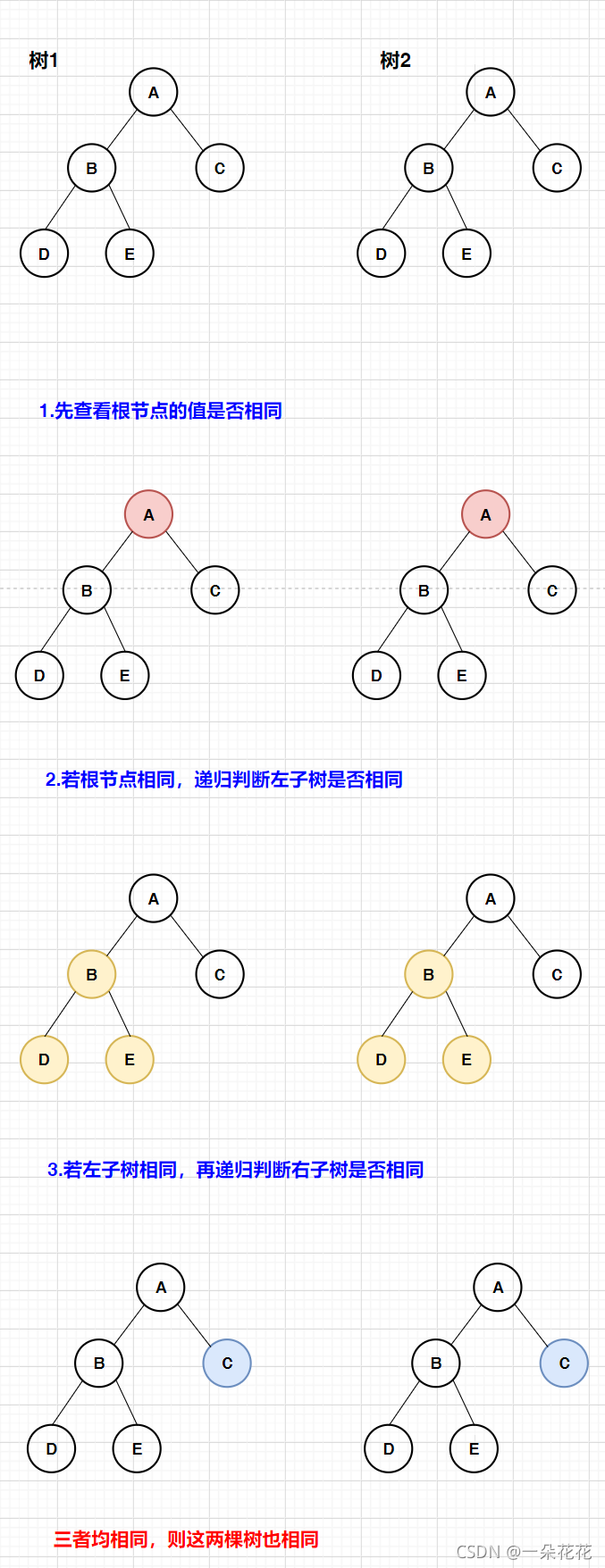
• 先判断根节点是否相同
• 遍历判断左子树是否相同
• 遍历判断右子树是否相同

以上条件均满足时，则说明这两棵树相同

画图分析：

代码实现：

    public boolean isSameTree(TreeNode p, TreeNode q) {
        //两棵树全为空
        if(p == null && q == null){
            return true;
        }
        //一棵树为空
        if(p == null || q == null){
            return false;
        }
        //两棵树均不为空
        //先判断根节点是否相同
        if(p.val != q.val){
            return false;
        }
        return isSameTree(p.left,q.left) && isSameTree(p.right,q.right);
    }

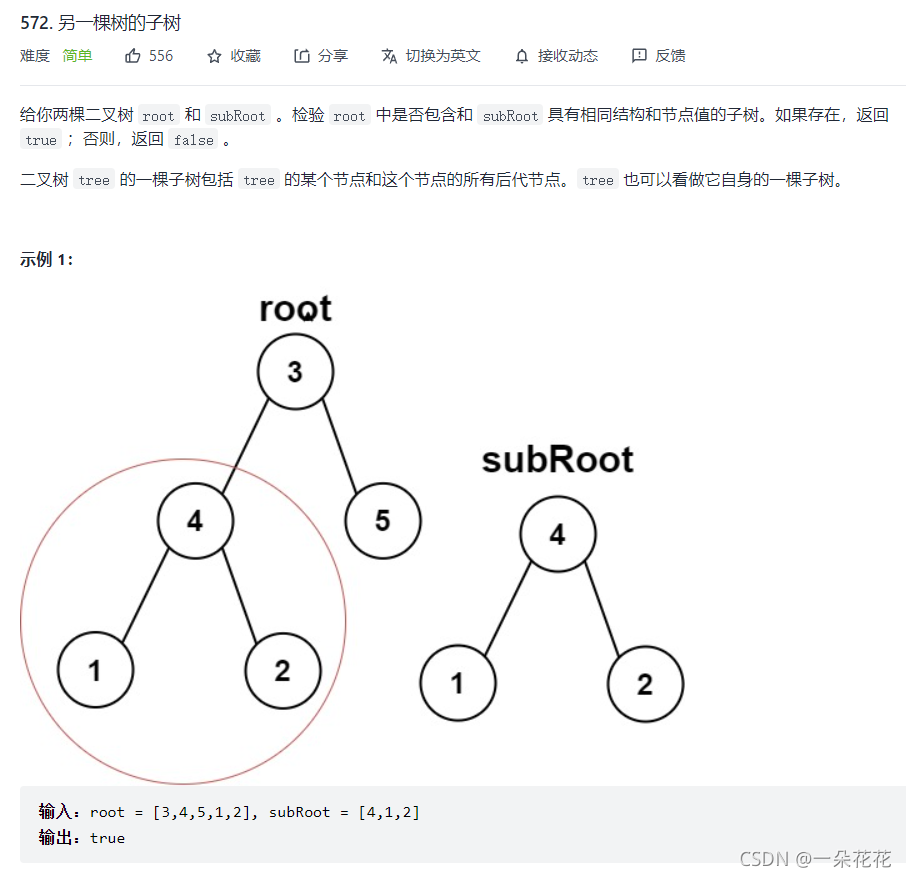
另一棵树的子树

题目：在线OJ

思考：

判断一棵树是不是另外一棵树的子树，本质就是在判断一棵树和另外一颗树的某个子树是否相等
可使用：遍历 + 递归拆分问题

• 先检查 root 和 subRoot 是否相等
• 检查 root.left 是否包含 subRoot
• 在检查 root.right 是否包含 subRoot

上述满足一个即可

画图：

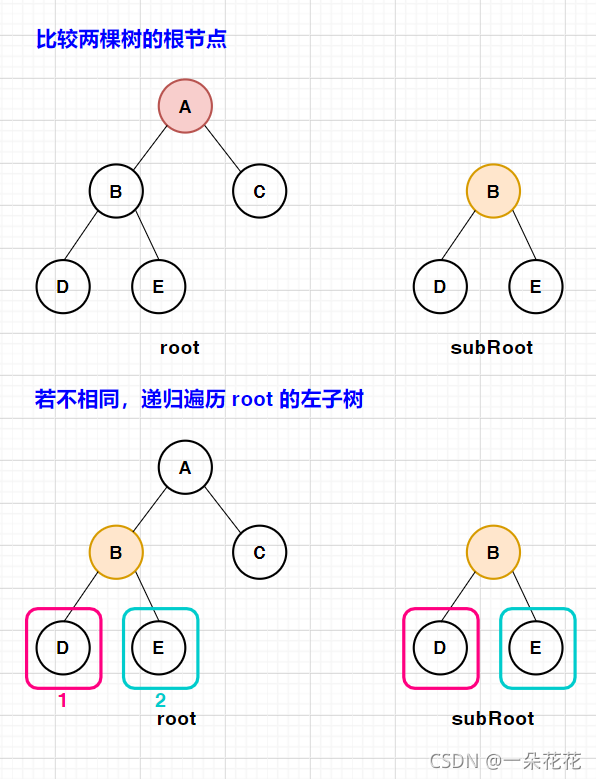
上述画了左子树的情况，若左子树在不相同，接着再递归右子树与子树比较，只要符合一种情况即可

代码实现：

public boolean isSubtree(TreeNode root, TreeNode subRoot) {
    //两棵树都为空
    if(root == null && subRoot == null){
        return true;
    }
    //一棵树为空
    if(root == null || subRoot == null){
        return false;
    }
    boolean ret = false;
    //根节点的值 相同
    if(root.val == subRoot.val){
        ret = isSameTree(root,subRoot);
    }

    return ret || isSubtree(root.left,subRoot) || isSubtree(root.right,subRoot);
}

二叉树的最大深度

题目：在线OJ

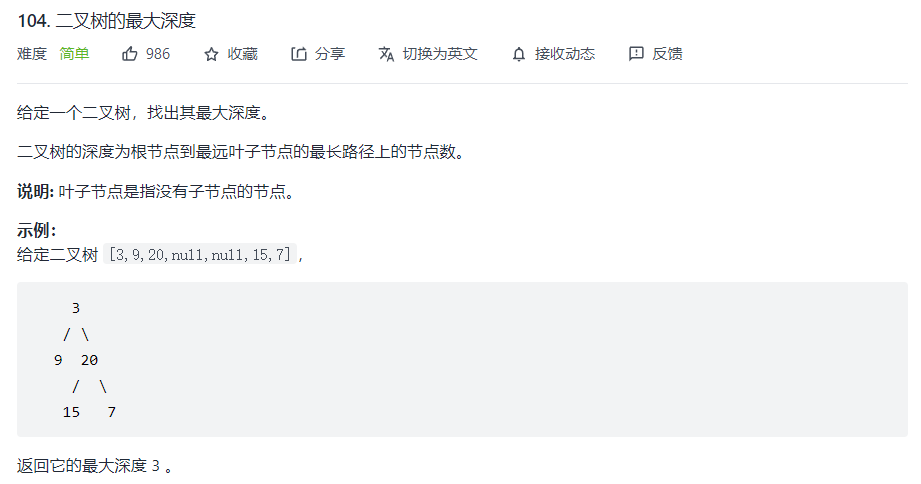
思考：

深度即：根节点到最远叶子节点的层数
此处要注意深度是从 0 开始算，还是从 1 开始算
二叉树的最大深度，即：max(左子树深度，右子树深度) + 1

代码实现：

    public int maxDepth(TreeNode root) {
        //空树
        if(root == null){
            return 0;
        }
        //左右子树为空 只有根节点
        if(root.left == null && root.right == null){
            return 1;
        }
        int leftDepth = maxDepth(root.left);
        int rightDepth = maxDepth(root.right);
        return 1 + (leftDepth > rightDepth ? leftDepth : rightDepth) ;
    }

平衡二叉树判断

题目：在线OJ

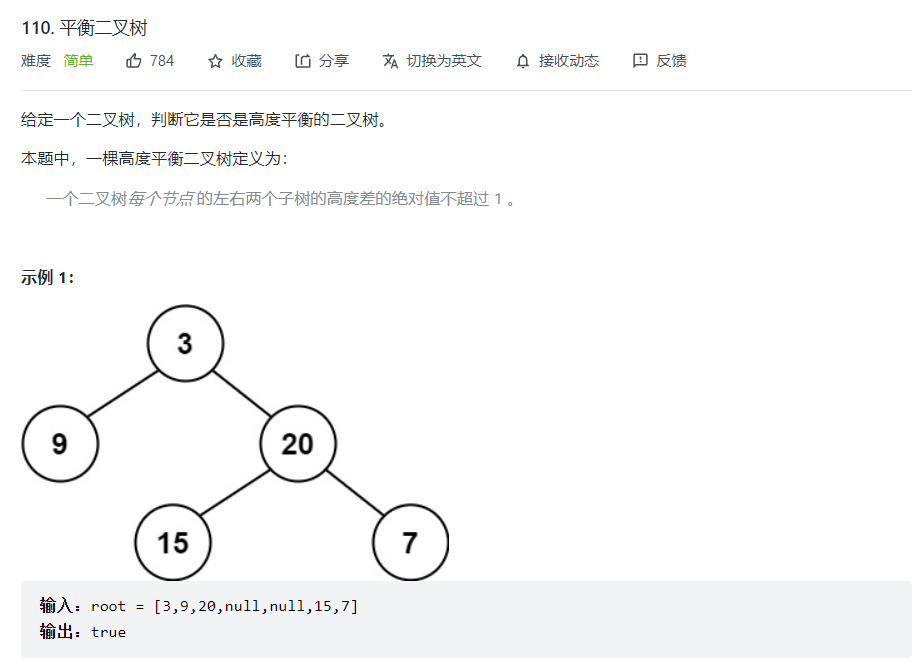
思考：

• 先判断空树，或没有子树(只有根节点)—平衡
• 针对当前节点，求左右子树高度差，看是否 ＞1
• 若 ＜1，再递归判断该树的左右子树，看高度差是否 ＜1

即：一棵树是否平衡，先判断该树自己的左右子树高度差是否 ≤ 1，还要满足左右子树也平衡才可以判断该树是平衡树

画图分析：

代码实现：

public boolean isBalanced(TreeNode root) {
    //空树
    if(root == null){
        return true;
    }
    //只有根节点  左右子树为空
    if(root.left == null && root.right == null){
        return true;
    }
    //判断当前节点对应的子树是否平衡
    int leftDepth = maxDepth(root.left);
    int rightDepth = maxDepth(root.right);
    if(leftDepth - rightDepth > 1 || leftDepth - rightDepth < -1){
        return false;
    }
    return isBalanced(root.left) && isBalanced(root.right);
}

对称二叉树

题目：在线OJ

思考：

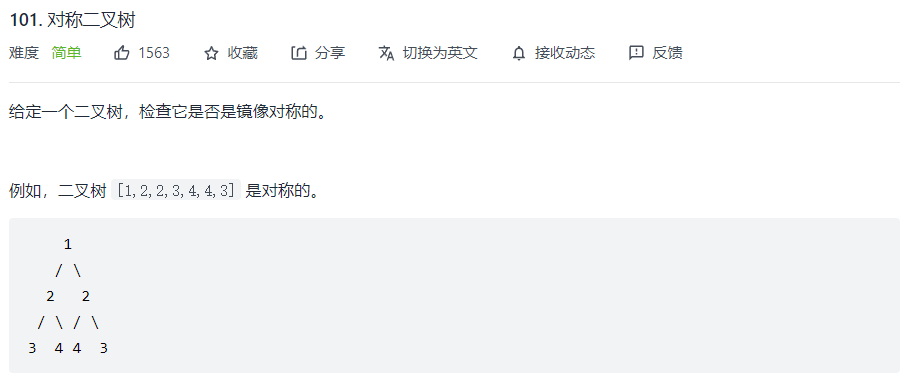
判断一棵树是否对称，本质上就是判断该树的所有子树是否对称

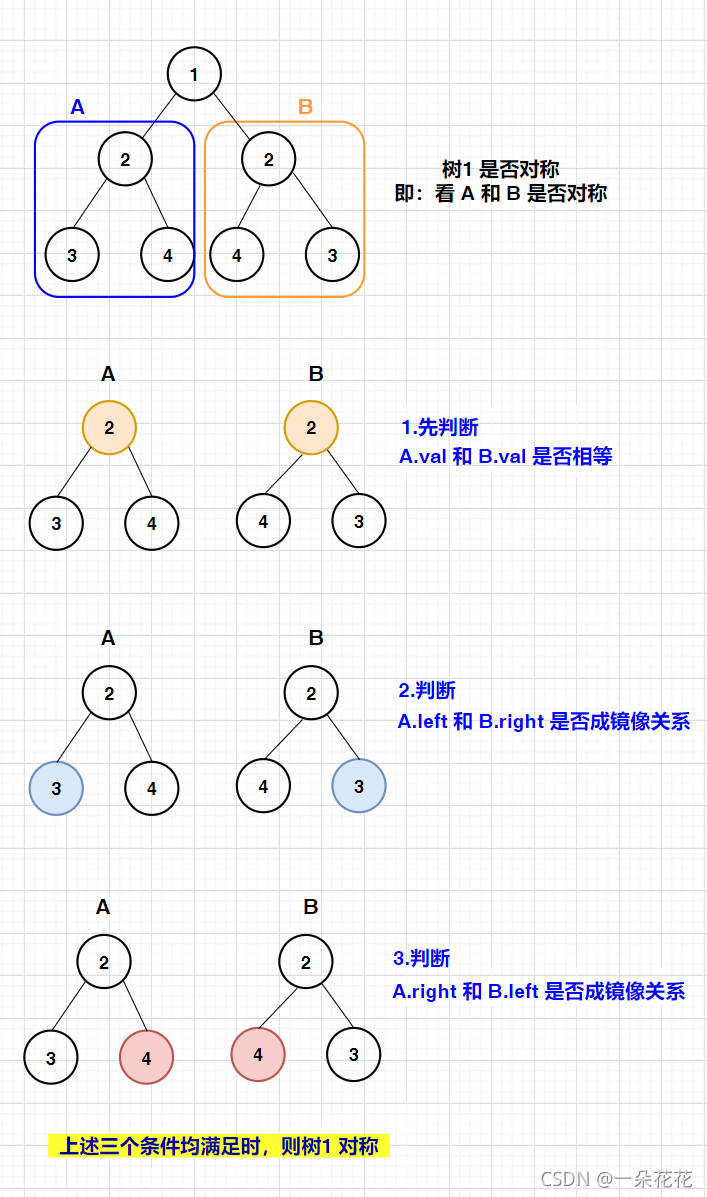
• 先判断左右子树( A B )的根节点是否相同
• 判断 A.left 和 B.right 是否成镜像关系
• 判断 A.right 和 B.left 是否成镜像关系

画图分析：

代码实现：

public boolean isSymmetric(TreeNode root) {
    //空树
    if(root == null){
        return true;
    }
    return isMirror(root.left,root.right);
}

public boolean isMirror(TreeNode t1,TreeNode t2){
    //左右子树都为空
    if(t1 == null && t2 == null){
        return true;
    }
    //一棵子树为空
    if(t1 == null || t2 == null){
        return false;
    }
    //两棵树的根节点 值不相等
    if(t1.val != t2.val){
        return false;
    }
    return isMirror(t1.left,t2.right) && isMirror(t1.right,t2.left);
}

进阶面试题

二叉树的遍历及构建

题目：在线OJ

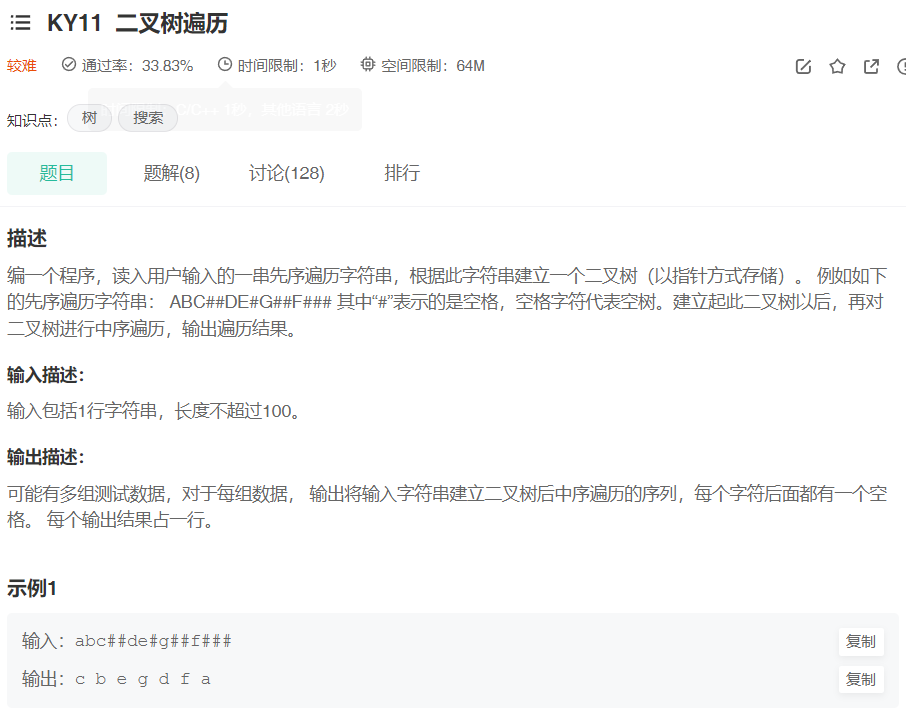
思考：

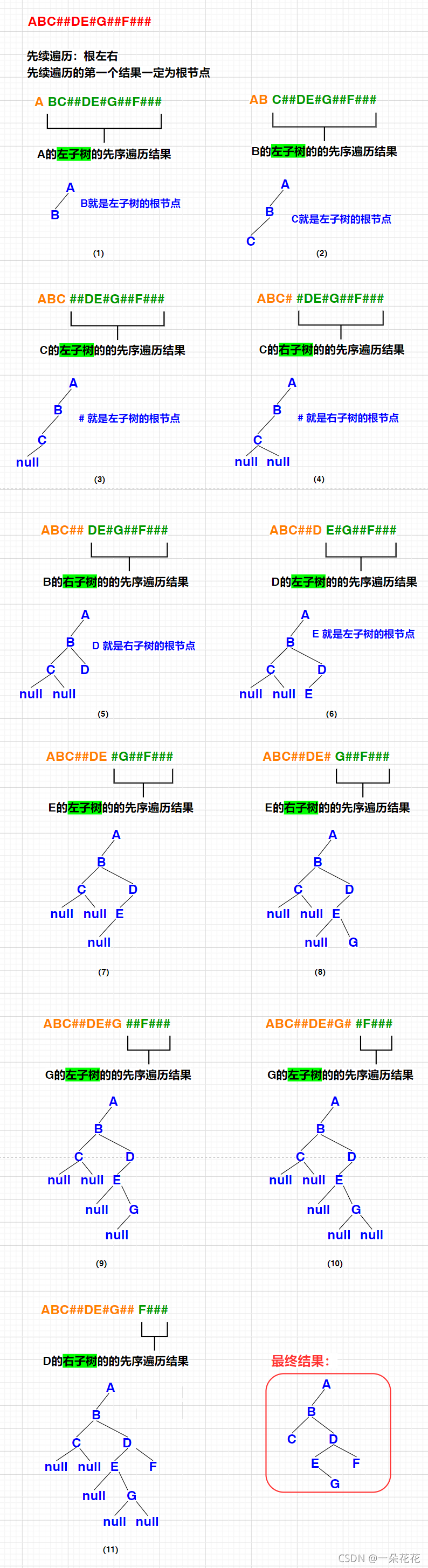
画图分析：

代码实现：

public class BuildTreeDemo {
    //静态内部类
    static class TreeNode{
        public char val;
        TreeNode left;
        TreeNode right;

        public TreeNode(char val) {
            this.val = val;
        }
    }

    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        //循环输入 在线OJ 一般都是多组用例
        while(scan.hasNext()){
            // s这个字符串就对应一对形如“abc##de#g##f###” 的输入数据
            String s = scan.next();
            TreeNode root = build(s);
            //中序遍历
            inOrder(root);
            System.out.println();
        }
    }

    private static void inOrder(TreeNode root) {
            //若为空树，直接返回
            if(root == null){
                return;
            }
            //递归访问左子树
            inOrder(root.left);
            //访问根节点
            System.out.print(root.val+" ");
            //递归访问右子树
            inOrder(root.right);
    }

    // index用来记录访问到 s 的哪个元素
    private static int index = 0;
    private static TreeNode build(String s) {
        index = 0;
        //先序遍历
        return createTreePrevOrder(s);
    }

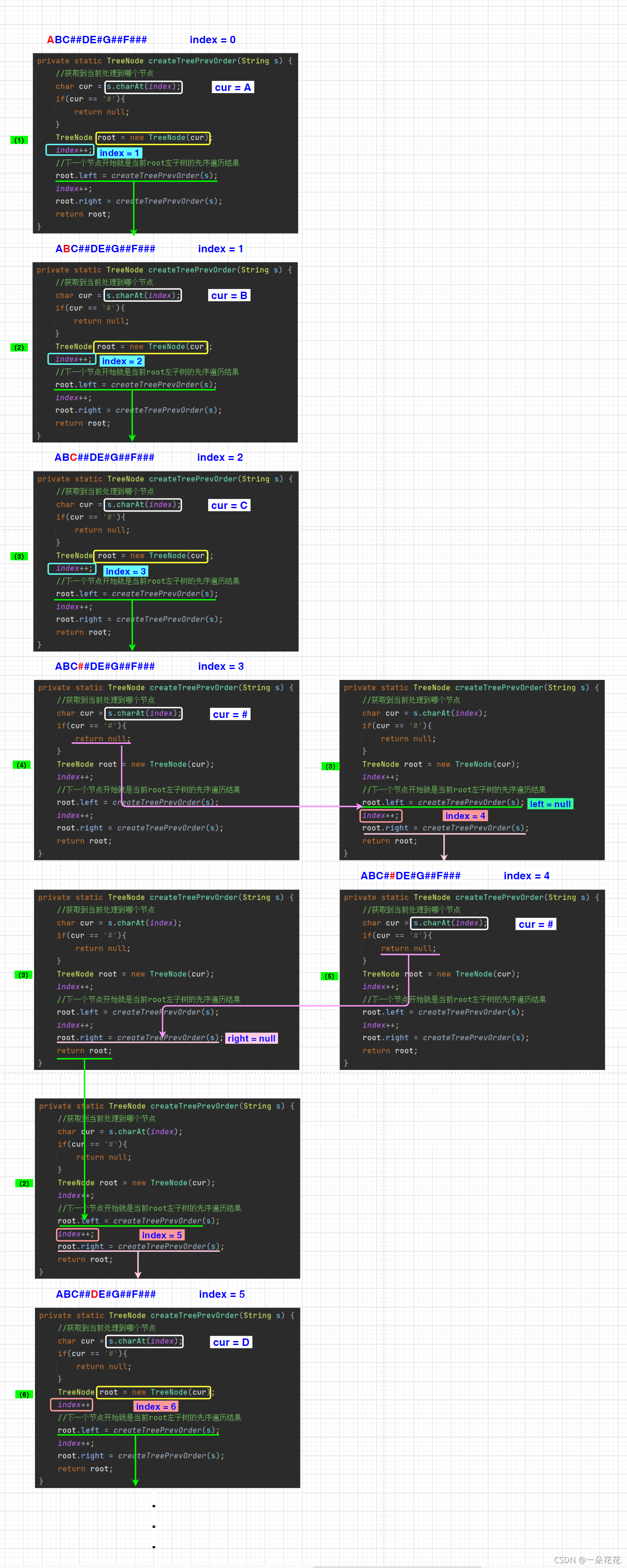
    private static TreeNode createTreePrevOrder(String s) {
        //获取到当前处理到哪个节点
        char cur = s.charAt(index);
        if(cur == '#'){
            return null;
        }
        TreeNode root = new TreeNode(cur);
        index++;
        //下一个节点开始就是当前root左子树的先序遍历结果
        root.left = createTreePrevOrder(s);
        index++;
        root.right = createTreePrevOrder(s);
        return root;
    }
}

部分递归过程分析：

二叉树的分层遍历

题目：在线OJ

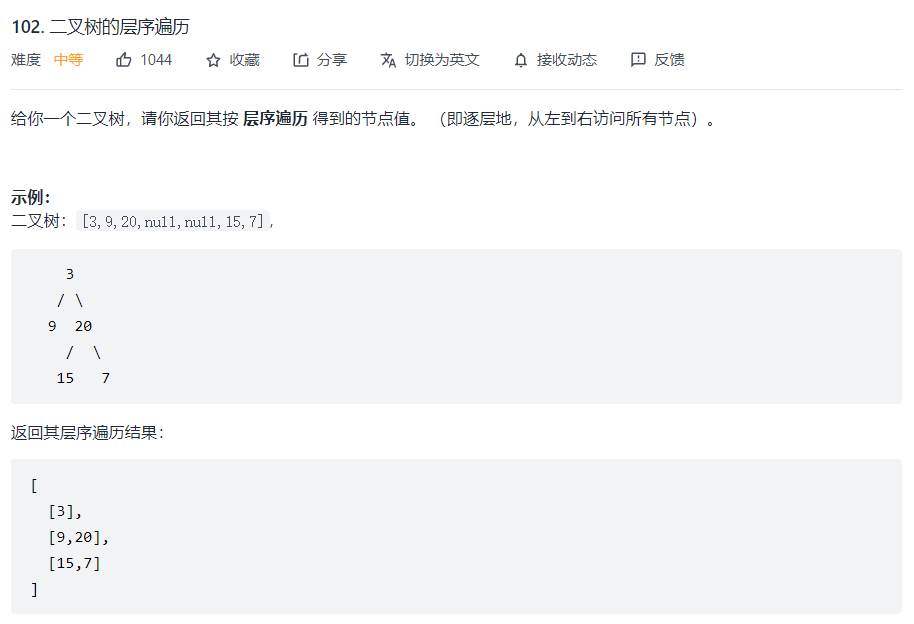
• 递归实现

思考：

创建一个变量 result 来存放我们的结果，最后 return result
(result 相当于一个二维数组，result 0 对应第0层节点，result 1 对应第1层节点…)

代码实现：

static List<List<Integer>> result = new ArrayList<>();
public List<List<Integer>> levelOrder(TreeNode root) {
    //清空result 因为result是全局变量
    result.clear();
    //空树判定
    if(root == null){
        return null;
    }
    // helper 方法辅助递归，第二个参数表示当前层数 从 0 开始算
    helper(root,0);
    return result;
}
private void helper(TreeNode root, int level) {
    if(level == result.size()){
        result.add(new ArrayList<>());
    }
    //把当前节点添加到 result 中的合适位置
    result.get(level).add(root.val);
    if(root.left != null){
        helper(root.left,level + 1);
    }
    if(root.right != null){
        helper(root.right,level + 1);
    }
}

代码分析：

• 非递归实现 (循环)

思考：

• 使用一个队列queue，先用来存放每一层的节点，并使用变量 level 来记录该层有几个元素
• 创建一个 list 来存放每一层节点，每遍历完一层，将每一层都入队列然后再出队列并将其移除，即：把队列里这一层的元素出队列，并将其加入到 list 中
• 判断左 / 右节点是否为空，来将下一层的元素加入到queue，队列为空，停止循环

代码实现：

public List<List<Integer>> levelOrder(TreeNode root){
    //创建一个 result 来存放结果
    List<List<Integer>> result = new ArrayList<>();
    //空树判断
    if(root == null){
        return result;
    }
    //创建一个队列，把根节点加入队列
    Queue<TreeNode> queue = new LinkedList<>();
    queue.add(root);
    //队列不为空，就一直循环
    while ( !queue.isEmpty()){
        //定义为一个 list 来存放每一层节点
        List<Integer> list = new ArrayList<>();
        //队列中当前所存在的数 即为当前层所有的数
        int level = queue.size();

        for (int i = 0; i < level; i++) {
            // 获得并将第一个节点出队列
            TreeNode cur = queue.poll();
            list.add(cur.val);
            if(cur.left != null){
                queue.add(cur.left);
            }
            if(cur.right != null){
                queue.add(cur.right);
            }
        }
        result.add(list);
    }
    return result;
}

二叉树的最近公共祖先

题目：在线OJ

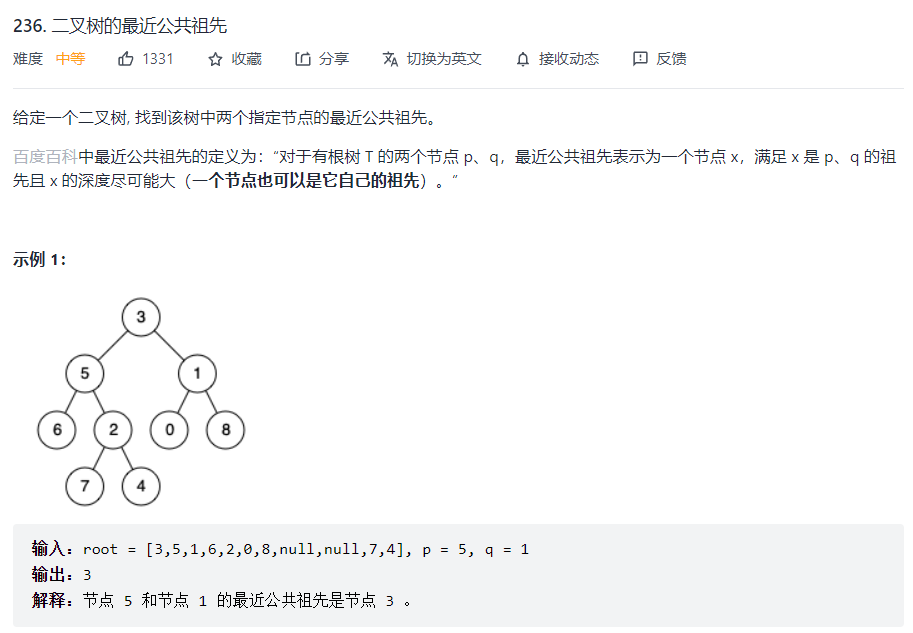
• 方法1

思考：

若从某个节点开始，后续遍历能把 p 和 q 都找到，说明该节点就是 p 和 q 的公共祖先
若从某个节点开始，后续遍历能把 p 和 q 都找到，并且 p 和 q 不在同一子树中，则当前节点就是 p 和 q 的最近公共祖先

代码实现：

private TreeNode lca = null;
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
    //空树判断
    if(root == null){
        return null;
    }
    // findNode方法，在递归寻找的过程中，找到结果，就将结果放到 lca 中
    findNode(root,p,q);
    //返回 lca
    return lca;
}
//从 root 出发找 p q,只要找到 1 个，就返回true，都找不到返回false
private boolean findNode(TreeNode root, TreeNode p, TreeNode q) {
    //空树判断
    if(root == null){
        return false;
    }
    // 递归 后序遍历查找
    int left = findNode(root.left,p,q) ? 1 : 0;
    int right = findNode(root.right,p,q) ? 1 : 0;
    int mid = (root == p || root == q) ? 1 : 0;
    if(left + right + mid == 2){
        lca = root;
    }
    return (left + right +mid) > 0;
}

• 方法2

思考：

• 在左 右子树查找是否包含 p，q，如果 p 和 q 不在同一子树中，那么此时的根节点就是最近公共祖先
• 如果左子树包含 p 和 q，那么到当前节点的左子树中查找，最近公共祖先在左子树里面
• 如果右子树包含 p 和 q，那么到当前节点的右子树中查找，最近公共祖先在右子树里面

代码实现：

public TreeNode lowestCommonAncestor2(TreeNode root, TreeNode p, TreeNode q) {
    if (root == null || p == root || q == root) {
        return root;
    }
    TreeNode left = lowestCommonAncestor(root.left, p, q);
    TreeNode right = lowestCommonAncestor(root.right, p, q);

    if (left != null && right != null) {
        return root;
    }
    return left == null ? right : left;
}

二叉搜索树与双向链表

题目：在线OJ①，在线OJ②

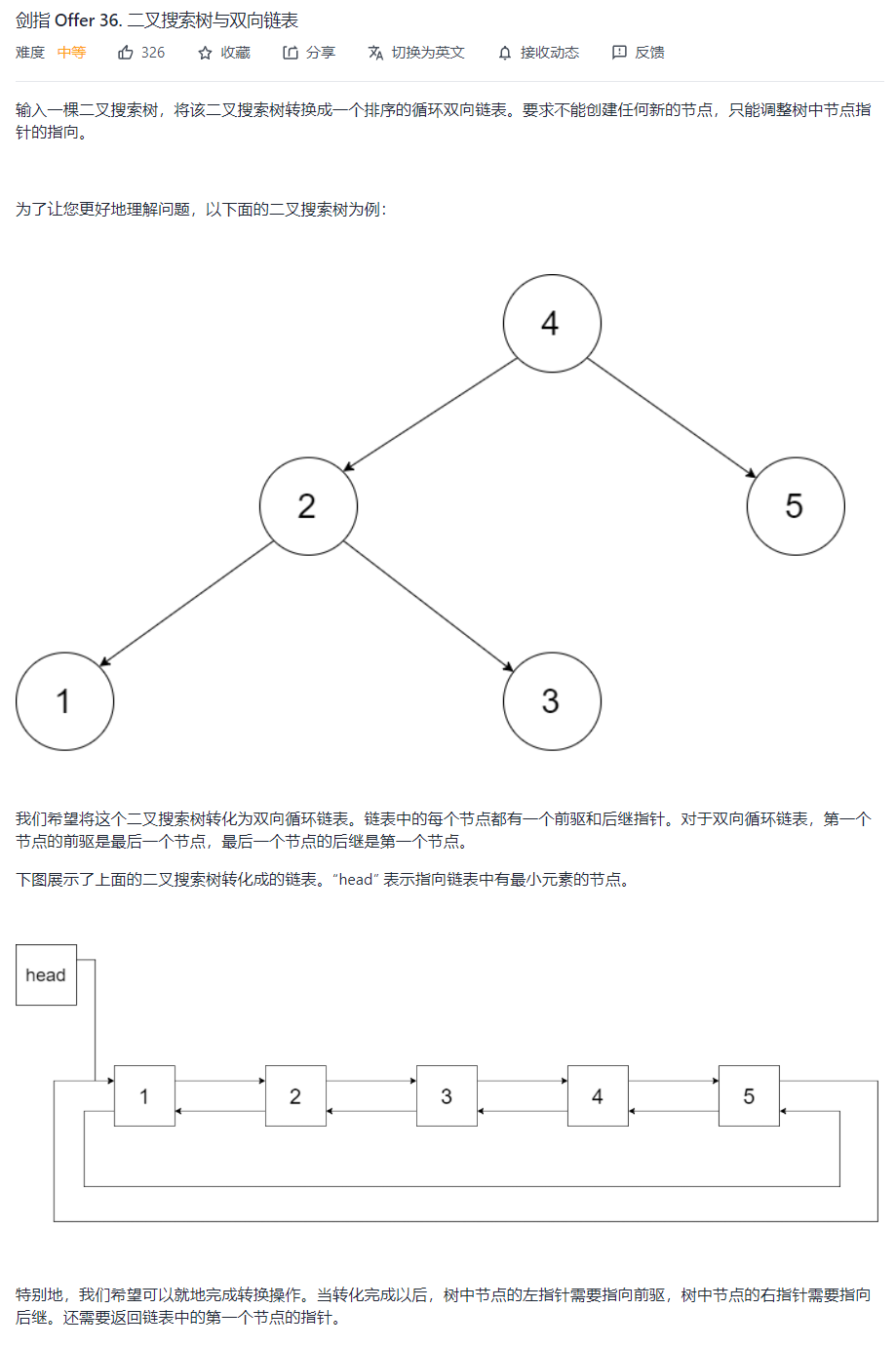
思考：

首先，我们要知道二叉搜索树的概念
二叉搜索树：是一种特殊的二叉树，对于树上的任意节点，它都满足：左子树中的所有节点都小于根节点，根节点又小于右子树中的所有节点
因此，若对一个二叉搜索树进行中序遍历，遍历结果就是一个有序数组

• 递归处理左子树，把左子树和当前节点连在一起
  left 就是左子树这个链表的根节点
• 递归转换右子树，把当前节点和右子树连在一起
  right 相当于链表中的 next
• 最后返回链表的头节点

树中没有 next 和 prev，我们使用 right 指向下一个节点，left 指向上一个节点

代码实现：

public TreeNode Convert(TreeNode pRootOfTree) {
    //空树判断
    if(pRootOfTree == null){
        return null;
    }
    //只有根节点
    if(pRootOfTree.left == null && pRootOfTree.right == null){
        return pRootOfTree;
    }
    //中序遍历二叉搜索树
    // 得到一个有序的数组

    //递归处理左子树
    // left 就是左子树这个链表的根节点
    TreeNode left = Convert(pRootOfTree.left);
    // 找到左子树这个链表的尾节点
    TreeNode leftTail = left;
    // right 相当于 next
    while(leftTail != null && leftTail.right != null){
        leftTail = leftTail.right;
    }
    //循环结束后，leftTail 指向左边链表的尾部

    //把左子树和当前节点连在一起
    if (left != null){
        leftTail.right = pRootOfTree;
        pRootOfTree.left = leftTail;
    }
    //递归转换右子树
    TreeNode right = Convert(pRootOfTree.right);
    if (right != null){
        right.left = pRootOfTree;
        pRootOfTree.right = right;
    }
    //返回链表的头节点
    // left 为空，链表头节点就是 root
    // left 非空，链表头节点就是 left
    return left == null ? pRootOfTree : left;
}

从前序与中序遍历序列构造二叉树

题目：在线OJ

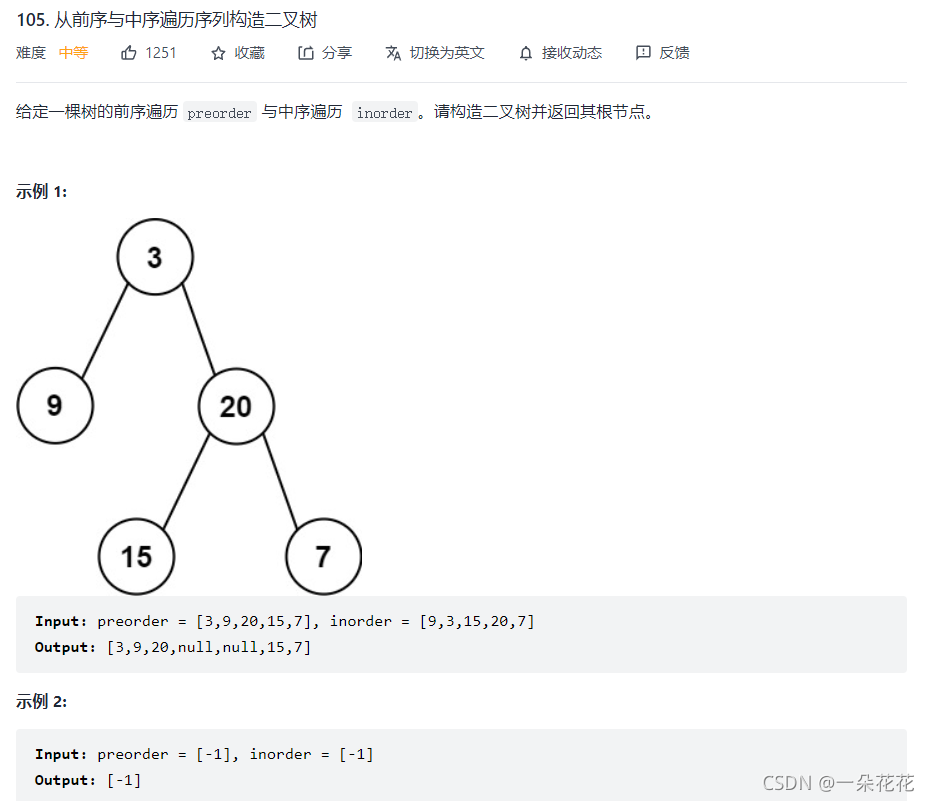
思考：

先序遍历：第一个访问的节点一定是根节点，后面的节点就是左子树 / 右子树的根节点
中序遍历：第一个访问的节点是树的最左侧节点，左子树一定在根节点左侧，右子树一定在根节点右侧

由以上两条规律，可以得出基本思路：

• 根据先序遍历结果找到当前树的根节点
• 拿到这个根节点到中序遍历结果中查找，找到其左 / 右子树
• 再根据划分结果来构造树

代码实现：

private int index = 0; //表示当前访问到 先序遍历结果的第几个元素
public TreeNode buildTree(int[] preorder, int[] inorder) {
    index = 0;
    return buildTreeHelper(preorder,inorder,0,inorder.length);
}
// [left,right) 区间表示 当前 preorder[index] 这个节点对应的子树的中序遍历结果
private TreeNode buildTreeHelper(int[] preorder, int[] inorder, int left, int right) {
    //中序遍历结果为空，这个树就是空树
    if(left >= right){
        return null;
    }
    //遍历元素结束
    if(left >= preorder.length){
        return null;
    }
    //根据当前节点的值创建根节点
    TreeNode root = new TreeNode(preorder[index]);
    //节点创建完毕，index++
    index++;
    //根据该节点在中序遍历结果的位置，把 inorder 数组划分成两个部分
    int pos = find(inorder,left,right,root.val);
    
    // [left,pos) 表示当前root左子树的中序遍历结果
    // [pos+1,right) 表示当前root右子树的中序遍历结果

    //递归构建
    root.left = buildTreeHelper(preorder,inorder,left,pos);
    root.right = buildTreeHelper(preorder,inorder,pos+1,right);
    return root;
}
private int find(int[] inorder,int left,int right,int toFind){
    for (int i = left; i < right; i++) {
        if(inorder[i] == toFind){
            return i;
        }
    }
    return -1;
}

从中序与后序遍历序列构造二叉树

题目：在线OJ

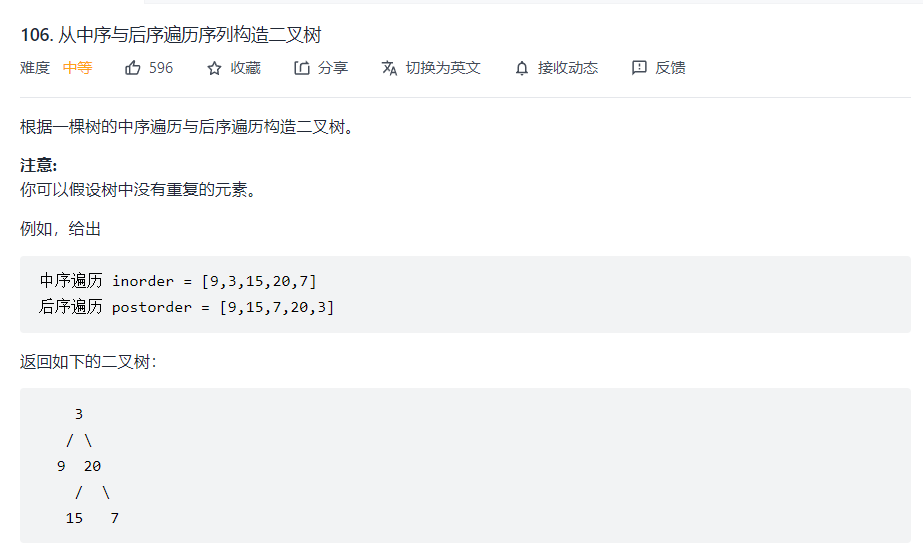
思考：

与上一题思路一样
中序遍历：第一个访问的节点是树的最左侧节点，左子树一定在根节点左侧，右子树一定在根节点右侧 (左根右)
后序遍历：最后一个访问的节点一定是根节点 (左右根)

思路：

• 将后续遍历结果逆置，就会变成一个镜像先序遍历结果 (根 右 左)
• 根据后序逆置遍历结果 找到当前树的根节点
• 拿到这个根节点到中序遍历结果中查找，找到其左 / 右子树
  再根据划分结果来构造树

根据二叉树创建字符串

题目：在线OJ

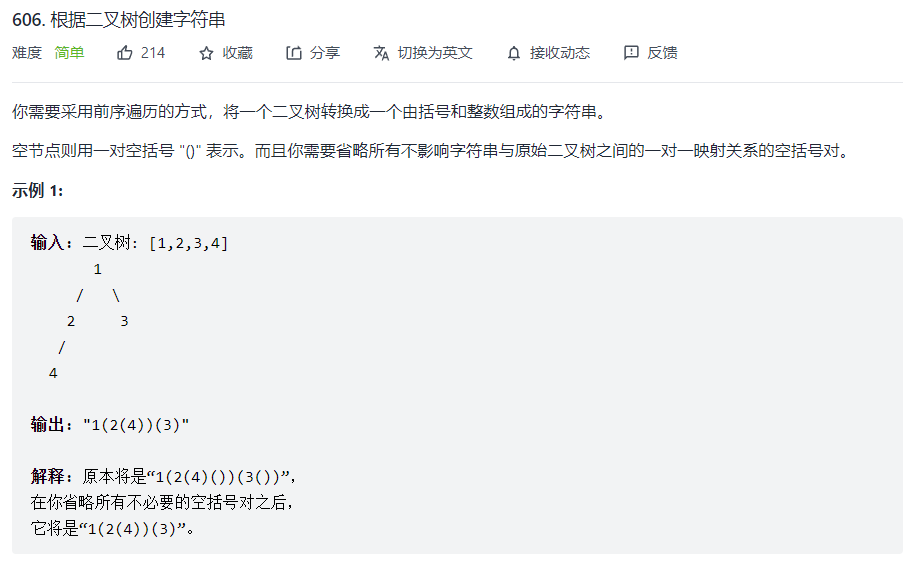
思考：

此处需要注意需要省略的括号：

• 若一个树左右子树都为空，就不需要把左右子树用 ( ) 表示
• 若一个树的左子树为空，右子树非空，需要把左子树用 ( ) 占位，且不能省略括号
• 若一个属的左子树非空，右子树为空，则可以省略 ( )

代码实现：

private StringBuilder sb = new StringBuilder();
public String tree2str(TreeNode root) {
    if(root == null){
        return ""; //此处注意不能为null，返回的是一个空字符串
    }
    helper2(root);
    sb.deleteCharAt(0);
    sb.deleteCharAt(sb.length() - 1);
    return sb.toString();
}
private void helper2(TreeNode root) {
    if(root == null){
        return;
    }
    //访问根节点 即：追加字符串
    sb.append("(");
    sb.append(root.val);

    //左子树
    helper2(root.left);
    // 左子树为空，右子树非空
    if(root.left == null && root.right != null){
        sb.append("()");
    }
    //右子树
    helper2(root.right);
    sb.append(")");
}