截止到目前我已经写了 600多道算法题,其中部分已经整理成了pdf文档,目前总共有1000多页(并且还会不断的增加),大家可以免费下载
下载链接:https://pan.baidu.com/s/1hjwK0ZeRxYGB8lIkbKuQgQ
提取码:6666
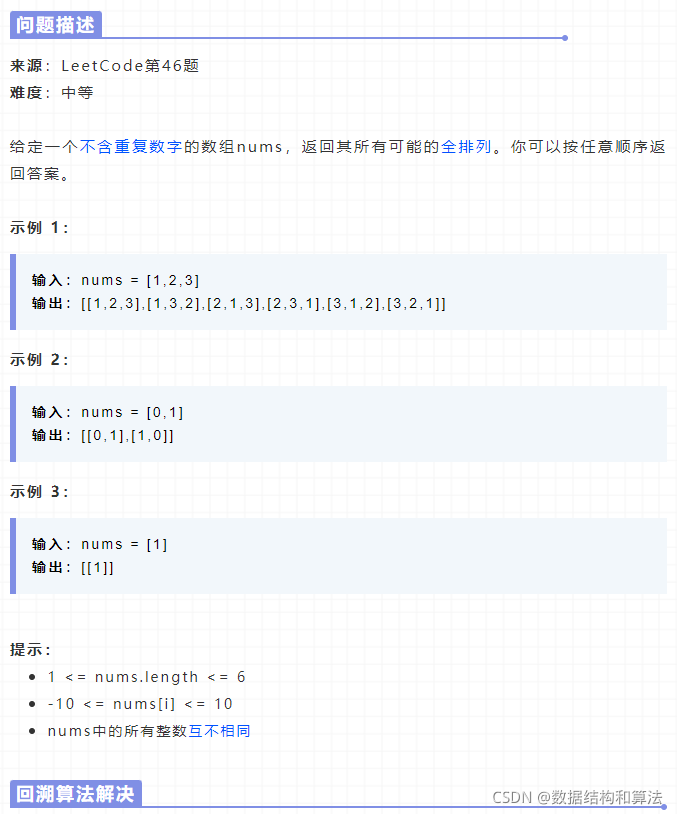
全排列也是一道经典的题,之前在讲450,什么叫回溯算法,一看就会,一写就废的时候,也提到过使用回溯算法来解决,具体细节可以看下。假设数组长度是n,我们可以把回溯算法看做是一颗n叉树的前序遍历,第一层有n个子节点,第二层有n-1个子节点……,来看个视频
视频链接
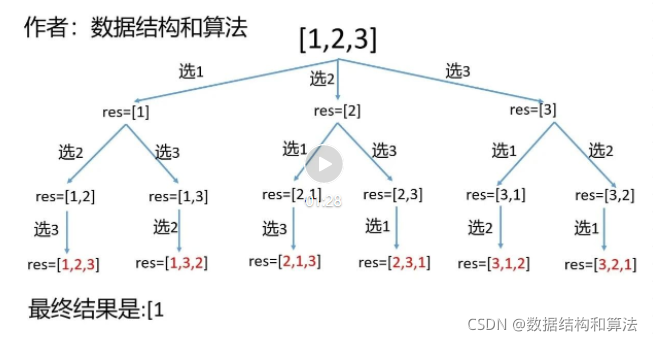
代码如下
public List<List<Integer>> permute(int[] nums) {
List<List<Integer>> list = new ArrayList<>();
backtrack(list, new ArrayList<>(), nums);
return list;
}
private void backtrack(List<List<Integer>> list, List<Integer> tempList, int[] nums) {
//终止条件,如果数字都被使用完了,说明找到了一个排列,(可以把它看做是n叉树到
//叶子节点了,不能往下走了,所以要返回)
if (tempList.size() == nums.length) {
//因为list是引用传递,这里必须要重新new一个
list.add(new ArrayList<>(tempList));
return;
}
//(可以把它看做是遍历n叉树每个节点的子节点)
for (int i = 0; i < nums.length; i++) {
//因为不能有重复的,所以有重复的就跳过
if (tempList.contains(nums[i]))
continue;
//选择当前值
tempList.add(nums[i]);
//递归(可以把它看做遍历子节点的子节点)
backtrack(list, tempList, nums);
}
}
我们就用数组[1,2,3]来测试一下,看一下打印结果
[1, 2, 3]
是不是很意外,示例1给出的是6个结果,这里打印的是1个,这是因为list是引用传递,当遍历到叶子节点以后要往回走,往回走的时候必须把之前添加的值给移除了,否则会越加越多,我们来看下视频
视频链接

再来看下代码
public List<List<Integer>> permute(int[] nums) {
List<List<Integer>> list = new ArrayList<>();
backtrack(list, new ArrayList<>(), nums);
return list;
}
private void backtrack(List<List<Integer>> list, List<Integer> tempList, int[] nums) {
//终止条件,如果数字都被使用完了,说明找到了一个排列,(可以把它看做是n叉树到
//叶子节点了,不能往下走了,所以要返回)
if (tempList.size() == nums.length) {
//因为list是引用传递,这里必须要重新new一个
list.add(new ArrayList<>(tempList));
return;
}
//(可以把它看做是遍历n叉树每个节点的子节点)
for (int i = 0; i < nums.length; i++) {
//因为不能有重复的,所以有重复的就跳过
if (tempList.contains(nums[i]))
continue;
//选择当前值
tempList.add(nums[i]);
//递归(可以把它看做遍历子节点的子节点)
backtrack(list, tempList, nums);
//撤销选择,把最后一次添加的值给移除
tempList.remove(tempList.size() - 1);
}
}
我们来看一下运行结果
[1, 2, 3]
[1, 3, 2]
[2, 1, 3]
[2, 3, 1]
[3, 1, 2]
[3, 2, 1]
这题使用回溯算法的还一种解决方式就是交换,比如我们先选择第一个数字,然后和后面的所有数字都交换一遍,这样全排列的第一位就确定了。然后第二个数字在和后面的所有数字交换一遍,这样全排列的第二位数字也确定了……,一直继续下去,直到最后一个数字不能交换为止,这里画个图来看一下
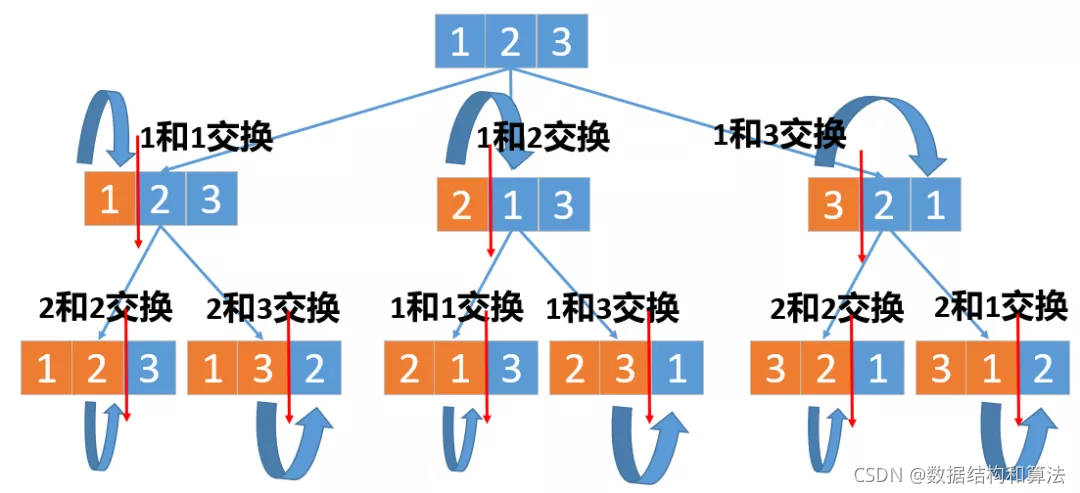
来看下代码
public List<List<Integer>> permute(int[] nums) {
List<List<Integer>> res = new ArrayList<>();
backtrack(nums, 0, res);
return res;
}
public void backtrack(int[] nums, int index, List<List<Integer>> res) {
//到最后一个数字,没法再交换了,直接把数组转化为list
if (index == nums.length - 1) {
//把数组转为list
List<Integer> tempList = new ArrayList<>();
for (int num : nums)
tempList.add(num);
//把list加入到res中
res.add(tempList);
return;
}
for (int i = index; i < nums.length; i++) {
//但前数字nums[index]要和后面所有的数字都要交换一遍(包括
// 他自己)
swap(nums, index, i);
//递归,数组[0,index]默认是已经排列好的,然后从index+1开始
//后面元素的交换
backtrack(nums, index + 1, res);
//还原回来
swap(nums, index, i);
}
}
//交换两个数字的值
private void swap(int[] nums, int i, int j) {
if (i != j) {
nums[i] ^= nums[j];
nums[j] ^= nums[i];
nums[i] ^= nums[j];
}
}
递归解决
我们来思考这样一个问题,假如数组[1,2,3],我们知道了[2,3]的全排列结果,只需要把1放到这些全排列的所有位置,即是数组[1,2,3]的全排列,画个图来看一下
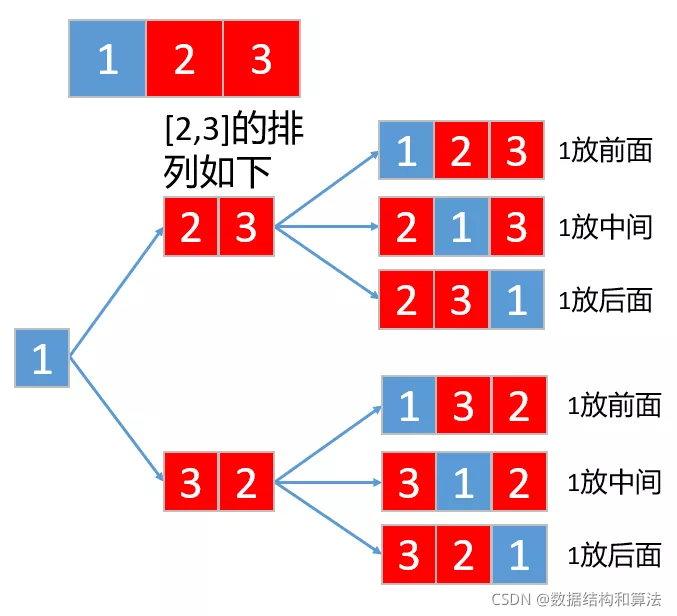
//递归解决
public List<List<Integer>> permute(int[] nums) {
return helper(nums, 0);
}
/**
* @param nums
* @param index 递归当前数字的下标
* @return
*/
private List<List<Integer>> helper(int[] nums, int index) {
List<List<Integer>> res = new ArrayList<>();
//递归的终止条件,如果到最后一个数组,直接把它放到res中
if (index == nums.length - 1) {
//创建一个临时数组
List<Integer> temp = new ArrayList<>();
//把数字nums[index]加入到临时数组中
temp.add(nums[index]);
res.add(temp);
return res;
}
//计算后面数字的全排列
List<List<Integer>> subList = helper(nums, index + 1);
//集合中每个子集的长度
int count = subList.get(0).size();
//遍历集合subList的子集
for (int i = 0, size = subList.size(); i < size; i++) {
//把当前数字nums[index]添加到子集的每一个位置
for (int j = 0; j <= count; j++) {
List<Integer> temp = new ArrayList<>(subList.get(i));
temp.add(j, nums[index]);
res.add(temp);
}
}
return res;
}