快速排序(Quicksort)
1.解释
<1>定义
快速排序(Quicksort)是对冒泡排序算法的一种改进。
它的基本思想是:
通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以== 递归== 进行,也可以利用栈以此达到整个数据变成有序 序列 。
<2>时间复杂度分析
快速排序在最坏情况下的 时间复杂度 和冒泡排序一样,是O (n^2),实际上每次比较都需要交换,但是这种情况并不常见。. 我们可以思考一下如果每次比较都需要交换,那么数列的平均时间复杂度是 O (nlogn) ,事实上在大多数时候,排序的速度要快于这个平均时间复杂度。. 这种算法实际上是一种分治法思想,也就是分而治之,把问题分为一个个的小部分来分别解决,再把结果组合起来。
2.图解
(1)图示解释




蓝色为已经排序好的数
暖色为当前基准数
红色为匹配失败的数
绿色为匹配成功的数
(2)每一趟的目的
每一趟是为了将我们选择的基准数的左边都比基准数小,右边都比基准数大
而每趟分为两部分再分别对这两部分进行下一趟的排序,这样到最后即为排序好的数组
(3)过程图示
牢记我们的目的是把基准数左边变成都比基准数小,右边变成都比基准数大
首先以最右边为基准数(实际上可随机),从右向左查找比基准数12小的
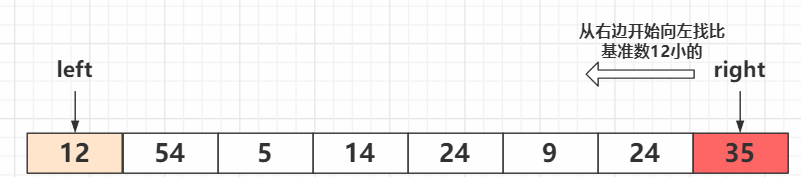
35,24比12大,right减小

查找到9比12小

12与9交换位置
交换后开始left向右查找比基准数12大的数

9不满足,继续查找

54满足

交换位置


再交换方向,从右边再开始向左查找比基准数12小的

24不满足,继续查找

14大于12不满足,继续查找

5满足,交换位置
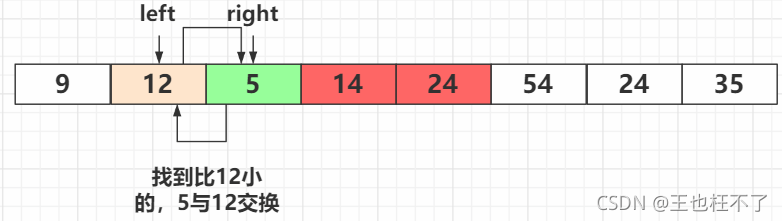
交换位置后

继续交换方向,牢记我们的目的是把基准数左边变成都比基准数小的,右边变成都比基准数大的
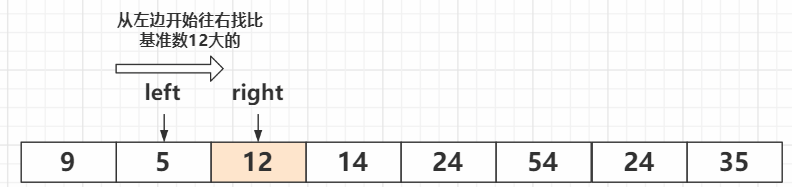
当left与right到达同一位置,意味着这一趟已经排序完成,此时基准数左边变成都比基准数小,右边变成都比基准数大,随后开始下一趟

再以基准数为界限,分别对左右进行下一趟排序,依此类推

排序后

完整代码
1.递归
通过观察过程我们得知,每一次基准数的位置一定是在left或者right上,故我们可以省略记录基准数,每次移动left时,以right下标所在位置的数一定是基准数,每次移动right时,以left下标所在位置的数一定是基准数,故有以下参考代码
#include<iostream>
using namespace std;
const int MaxSize=100;
class List
{
private:
int r[MaxSize+1];
int n;
public:
List(){n=0;} //empty list
void InsertR(int k) //�����
{ r[++n]=k;}
void Display(); //display
void QuickSort(int first,int end); //quickSort
void QuickSort()
{
QuickSort(1,n);
}
int qqq(int first ,int end);
};
void List::Display()
{
for(int i=1;i<=n;i++)
cout<<r[i]<<" ";
cout<<"\n";
}
void List::QuickSort(int first,int end) //quickSort
{
if(first<end)
{
int p = qqq(first,end);
QuickSort(first,p-1);
QuickSort(p+1,end);
}
}
int List::qqq(int first ,int end)
{
int i =first,j=end,temp;
while(i<j)
{
while(i<j&&r[i]<=r[j])j--;
if(i<j){
temp = r[i];
r[i] = r[j];
r[j] = temp;
i++;
}
while(i<j&&r[i]<=r[j])i++;
if(i<j){
temp = r[i];
r[i] = r[j];
r[j] = temp;
j--;
}
} Display();
return i;
}
int main()
{
List L;
while(1)
{
int k;
cin>>k;
if(!k) break;
L.InsertR(k);
}
//L.Display();
L.QuickSort();
//L.Display();
return 0;
}
/*
Input
Output
Sample Input
12 21 32 2 4 24 21 432 23 9 0
Sample Output
9 4 2 12 32 24 21 432 23 21
2 4 9 12 32 24 21 432 23 21
2 4 9 12 32 24 21 432 23 21
2 4 9 12 21 24 21 23 32 432
2 4 9 12 21 24 21 23 32 432
2 4 9 12 21 23 21 24 32 432
2 4 9 12 21 21 23 24 32 432 */
2.栈
栈的原理与递归其实一致,只不过是利用栈的特性来实现和递归一样的效果
//quickSort*/
#include<bits/stdc++.h>
using namespace std;
const int MaxSize=100;
class List
{
private:
int r[MaxSize+1];
int n;
public:
List(){n=0;} //empty list
void InsertR(int k) //�����
{ r[++n]=k;}
void Display(); //display
void QuickSort(); //quickSort
};
void List::Display()
{
for(int i=1;i<=n;i++)
cout<<r[i]<<" ";
cout<<"\n";
}
void List::QuickSort()//quickSort
{
stack<int> S;
int first = 1,end = n;
S.push(1);
S.push(n);
while(!S.empty())
{
int j = S.top();
S.pop();
int i = S.top();
S.pop();
end = j;
first = i;
while(i<j)
{
while(i<j&&r[i]<=r[j])j--;
if(i<j){
int temp=r[i];
r[i]=r[j];
r[j]=temp;
i++;
}
while(i<j&&r[i]<r[j])i++;
if(i<j)
{
int temp=r[i];
r[i]=r[j];
r[j]=temp;
j--;
}
}
if(first<i-1)
{
S.push(first);
S.push(i-1);
}
if(i+1<end)
{
S.push(i+1);
S.push(end);
}
}
}
int main()
{
List L;
while(1)
{
int k;
cin>>k;
if(!k) break;
L.InsertR(k);
}
L.Display();
L.QuickSort();
L.Display();
return 0;
}
/*
Input
Output
Sample Input
12 21 32 2 4 24 21 432 23 9 0
Sample Output
12 21 32 2 4 24 21 432 23 9
2 4 9 12 21 21 23 24 32 432 */
``
喜欢请收藏点赞,关注王也枉不了一起深入学习算法与数据结构