大家好我们又见面了,这是c++入门2的第一课,话不多说,我们继续学习。
大纲
1.最大连续子段和问题
2.数字三角形问题
3.练习
1.最大连续子段和问题
连续子段{3} 子段和是 3
对于上面的序列连续子段有:
【问题描述】 给定n个整数(可正可负)组成的序列a1,a2,…,an,求该序列的最大的连续子段和。如果所有整数都是负 数,那么定义其最大子段和为0.

连续{3,-4} 子段和是-1
连续{3,-4,2} 子段和是1
连续{3,-4,2,10} 子段和是11
连续{-4} 子段和是-4
连续子段{-4,2} 子段和是-2
连续子段{-4,2,10} 子段和是8
连续子段{2} 子段和是2
连续子段{2,10} 子段和是12
连续子段{10} 子段和是10
【问题描述】 给定n个整数(可正可负)组成的序列a1,a2,…,an,求该序列的最大的连续子段和。如果所有整数都是负 数,那么定义其最大子段和为0.?
【解题思路1】暴力枚举 时间复杂度O(n^2)
双重for循环,第一层枚举子段的开头,第二层枚举子段的结尾

【解题思路2】动态规划
定义一个dp数组,定义dp[i]是以a[i]为结尾的最大连续子段和
3 -4 2 10
A 𝑁
① dp[1]是以a[1]结尾的最大连续子段和,dp[1]=3
② 以a[2]结尾的子段可以是a[1]a[2]也可以单独是a[2],由于a[1]值是大于0的,所以a[1]a[2]
的值会比a[2]大,dp[2]=dp[1]+a[2]=-1
③ 以a[3]为结尾的子段可以是a[3]接在a[2]的后面,也可以单独是a[3],由于dp[2]是小于0的
a[3]接在后面会使的dp[3]减小,所以a[3]单独存在会更大一些,dp[3]=a[3]=2
④ 以a[4]为结尾的子段可以是a[4]接在a[3]的后面,也可以单独是a[4],由于dp[3]是大于0的
a[4]接在后面会使的dp[4]增大,dp[4]=dp[3]+a[4]=12
【解题思路2】动态规划
定义一个dp数组,定义dp[i]是以a[i]为结尾的最大连续子段和
如果dp[i-1]>0,无论a[i]为何值,那么dp[i]=dp[i-1]+a[i]是最大
如果dp[i-1]<=0,无论a[i]为何值,dp[i]=a[i];
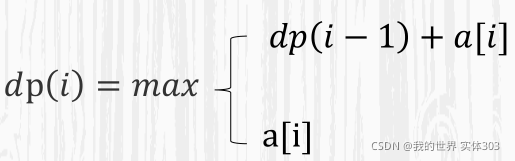
由此可写出代码

2.数字三角形问题
【 问题描述 】有一个由非负整数组成的三角形,第一行只有一个数,除了最下面一层之外每个数的左下方和右下方各有一个数,从第一行的数开始,每次可以往左下或右下走一格,直到走到最下行,把沿途经过的数全部加起来。如何走才能使得这个和尽量大?
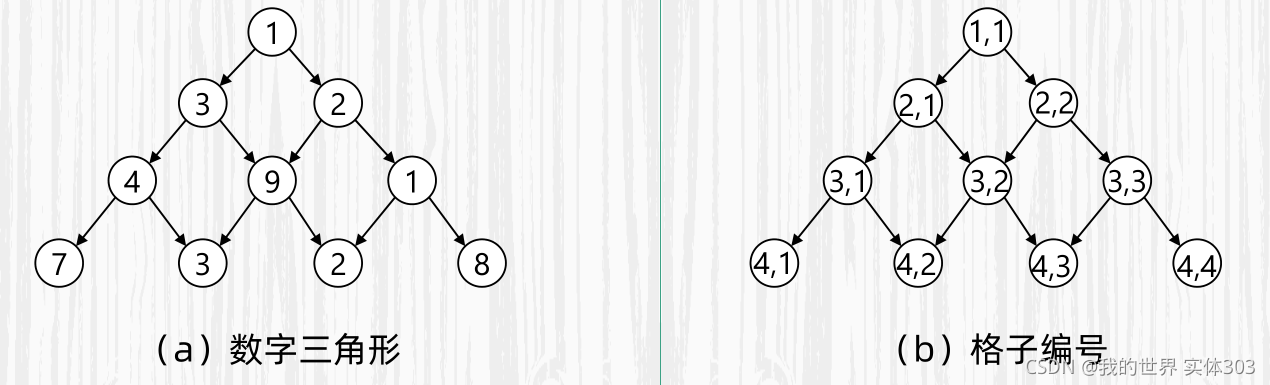
① 对于(2,1)来说,从(1,1)到(2,1)只有一条路径到达(2,1)的最大和是dp[2][1]=a[1][1]+a[2][1]
② 对于(2,2)来说,从(1,1)到(2,2)只有一条路径到达(2,2)的最大和是dp[2][2]=a[1][1]+a[2][2]
③ 对于(3,2)来说,可以从(2,1)过来也可以从(2,2)过来,要想使得和更大,选择从dp[2][1]与dp[2][2]的较大者过来,dp[3][2]=a[3][2]+max(dp[2][1],dp[2][2])
④ 对于(i,j)来说,可以从左上(i-1,j-1)的位置过来也可以从(i-1,j)过来,要想使得和更大,选择从较大者过来,dp[i][j]=a[i][j]+max(dp[i-1][j],dp[i-1][j])
⑤ 从(1,1)到(4,1)算是从顶层到达底层,同样到(4,2) (4,3) (4,4)都满足,问题的答案是dp[4][1]、dp[4][2]、dp[4][3]、dp[4][4]的最大值?
解题:
① 定义dp[i][j]为从(1,1)的位置到达(i,j)位置最大的
路径累加和
② dp[i][j] = a[i][j] + max (dp[i-1][j-1],dp[i-1][j])
③ 问题的解就是最下面一层dp[N][i]的最大值

3.例题
1.体验积分值
体验积分值
题目描述
卡卡西和小朋友们做完了烧脑的数字游戏,决定放松一下,他们来到了万达乐园,乐园中有很多的游玩项目,每玩一个项目就能获取一定的体验积分,不同的项目产生不同的体验积分,假设乐园所有的游乐项目正好排成一排,并且游客们不能游玩任意相邻的两个项目,那么卡卡西如何挑选游玩项目,使得这次万达行他能获得最多的体验积分值呢。解题:
题目要求不能玩两个连续的项目,也即使如果玩项目I,那么项目i-1 不能玩

定义dp[i]是游玩到第i个项目能够得到的最大积分值
① 对于第1个项目来说,dp[1]前面没有其他项目,所以dp[1]=a[1]=3;
② 对于第2个项目来说
? 如果玩项目2,就不能玩项目1,那么能够得到的项目积分是10
? 如果不玩项目2,则项目1就可以玩,那么能够得到的积分是3
? 显然前一种方案更划算,记录dp[2]=10,表示到第2个项目为止能够得到的最大积分值是10
③ 对于第3个项目来说
? 如果玩项目3,能够得到的积分是8,项目2就不能玩,但是项目1可以玩,玩到项目3为止得到的
积分是3+8=11
? 如果不玩项目2,那么项目2就可以玩,得到的积分值是10
? 显然前一种得到的积分值更大,记录dp[3]=11,表示到第3个项目为止能够得到的最大积分是11
④ 对于第4个项目来说
? 如果玩项目4,能够得到的积分是20,项目3就不能玩,那么玩到项目4为止体验积分是前两个项目的最大积分值dp[2]+20=30
? 如果不玩项目4,那么能够得到积分值是前3个项目的积分值dp[3]
? 显然前一种获得积分更大,记录dp[4]=30?
⑤ 对于第5个项目来说
? 如果玩项目5,能够得到的积分是21,项目4就不能玩,那么玩到项目5为止体验积分是前3个项目
的最大积分值dp[3]+21=32
? 如果不玩项目5,那么能够得到积分值是前4个项目的积分值dp[4]
? 显然前一种获得积分更大,记录dp[5]=32
对于第i个项目来说,
?如果玩项目i,能够得到的积分是a[i],项目i-1就不能玩了,那么玩到项目i为止能够到的的积分是前i-
2个项目的最大积分值dp[i-2]+a[i],
?如果不玩第i个项目,那么能够得到的积分值是前i-1个能够获得的最大积分值dp[i-1]
?那么dp[i]就是两种方案的较大者,即dp[i]=max(dp[i-2]+a[i],dp[i-1])

2.方案数
方案数
题目描述
有一个类似弹球的游戏,如下图所示。
小球从上向下滑落,每次到一个“交叉”点都有2种选择:向左或向右滑落。如果有一个球从顶端滑落到底,有多少种不同的方法?但是中间的一个“交叉”点有一些“陷阱”,小球滑到“陷阱”就不能继续下滑了。如果题目中不存在陷阱,那么此题就是数字三角形问题,ans = max (dp[n][i]) ,对于dp[i][j] =
max(dp[i-1][j-1],dp[i-1][j])
想一下,如果位置(i,j)处是陷阱的话,那么dp[i][j]应该等于什么?
dp[i][j] = 0 因为无论左上角和右上角的值是多大,都无法到达(i,j)这个位置
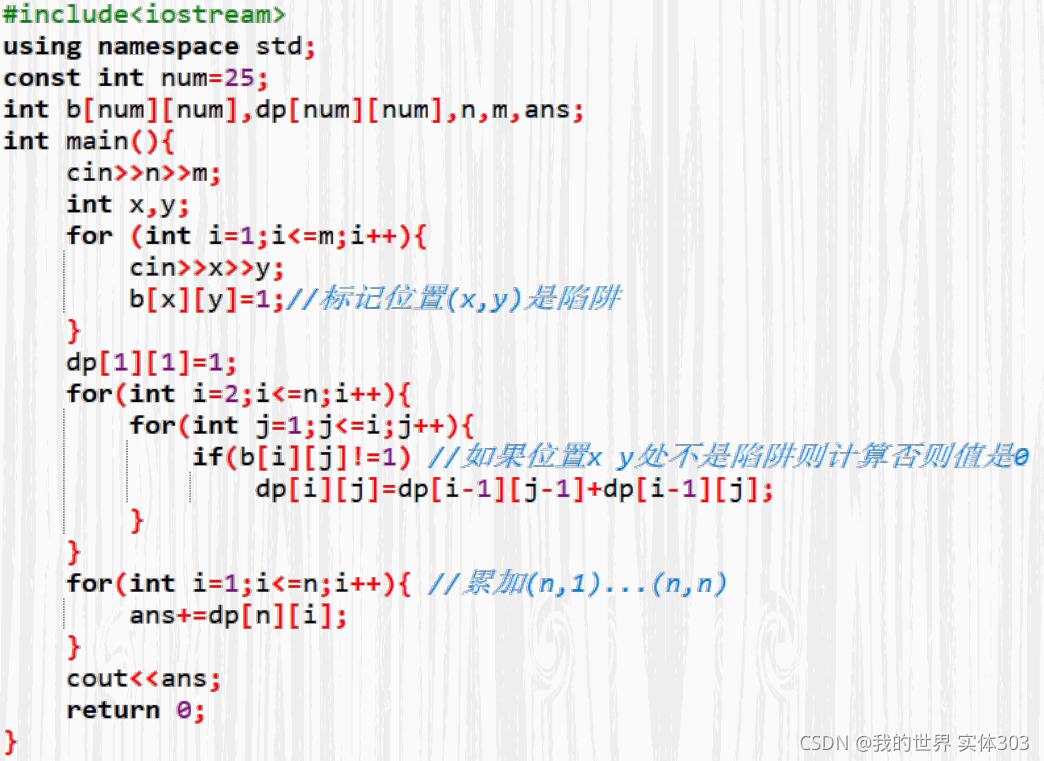
如果(i,j)处是陷阱的话dp[[i][j]=0 ,如果不是陷阱 dp[i][j]=max(dp[i-1][j-1],dp[i-1][j]),如何判断是不是陷阱?
陷阱的位置题目都给定了,只需要在读数据的时候,额外定义数组用来标记位置(i,j)
是不是陷阱,如果是陷阱就标记数组的值为1,如果不是就标记为0
到达底层任意一个位置都是到达底层了,所以方案数等于到达底层的所有方案的总和,即所以
dp[n][i]的和
好啦,这就是今天的内容了,再见了!