基于贪心算法的活动安排方案(含C++代码)
一、问题描述
假设某社团一天要组织n个活动E={1,2,3,…n},其中每个活动都要求使用同一礼堂,而且在同一时间内只有一个活动能使用这个礼堂。每个活动i都有一个要求使用礼堂的起始时间si和结束时间fi,且si<fi。如果选择活动i,则它在半开时间区间[si,fi)内占用资源。若区间[si,fi)与区间[sj,fj)不相交,则称活动i与活动j是相容的。现在给定n个活动的开始时间和结束时间,请设计一个活动安排方案,使得安排的相容活动数目最多。
二、思考
由于题目要求在固定时间内安排尽可能多的相容活动,本文将其归类为基于贪心算法的区间相交问题。首先,将fi作为度量指标,由小到大对所有活动进行排序,在将每一个活动的si与其前一个活动的fi进行比较,如果小于,则不能相容,舍弃该活动;如果大于,则可以相容,保存该活动。最后即可得到一个活动安排方案,使得安排的相容活动数目最多。
三、代码展示
代码:
#include<iostream>
using namespace std;
class process{
public:
int number;
int start;
int end;
};
int main(){
int n;
cout<<"请输入活动的个数:" ;
cin>>n;
process a[n];
for(int i=0;i<n;i++){
cout<<"请输入活动"<<i+1<<"的编号,开始时间与结束时间:"<<endl;
cin>>a[i].number;
cin>>a[i].start;
cin>>a[i].end;
}
//排序:将所有活动的结束时间按从小到大的顺序排列
process temp;
for(int i=0;i<n-1;i++){
for(int j=i+1;j<n;j++){
if(a[i].end>a[j].end){
temp=a[i];
a[i]=a[j];
a[j]=temp;
}
}
}
int count=1;
int cur=0;
for(int i=0;i<n;i++){
if(a[cur].end<=a[i].start){
count++;
cur=i;
cout<<"最多可相容的活动有"<<count<<"个,"<<"分别为:";
cout<<a[0].number<<","<<a[cur].number<<endl;
}
}
return 0;
}
运行截图:
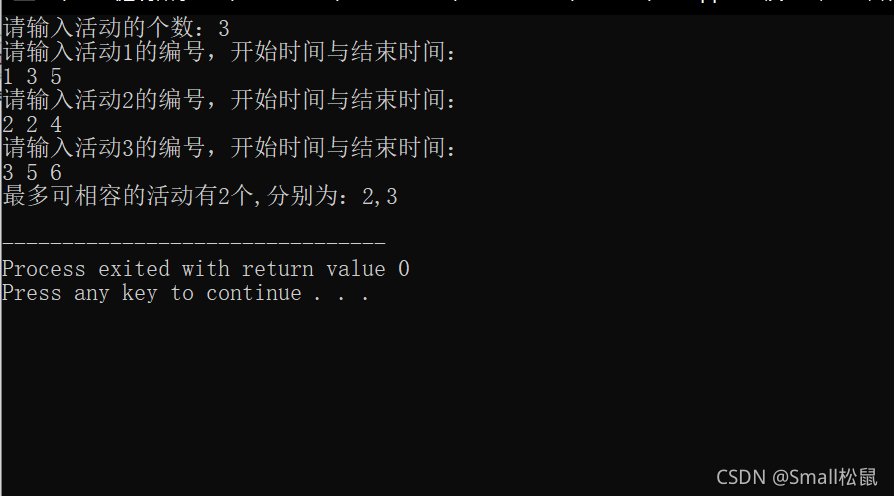
总结
这是算法老师上课出的题目,我借鉴了很多大佬对区间相交内容的理解(吼吼吼,就是代码),不知道有没有更好的方法,如果有的话希望大家可以和俺说说,如果有不对的地方,欢迎大家指正,十分感谢。