一、阻尼牛顿法使用条件?
阻尼牛顿法解决了保证不了迭代方向是下降方向这个问题。
采取的做法是确定了迭代方向(和牛顿法一样的迭代方向)之后,还需要在该方向做一维搜索,寻找使得在该迭代方向上最优的迭代步长。
公式如下:
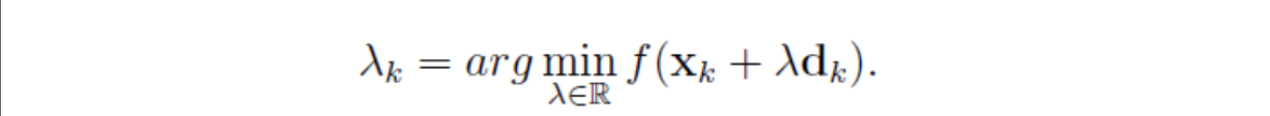
二、算法及matlab程序
1.算法
1.给定终止误差值0≤??1,δ∈(0,1),σ∈(0,0.5),δ∈(0,1),σ∈(0,0.5),
初始化x0∈Rn,设k=0.
2.计算gk=?f(xk),若||gk||≤?,则停止,输出x?≈xk
3.计算Gk=?2f(xk),求关于gk与Gk的比,Gk*dk=?gk
4.设mkmk是不满足下列不等式的最小非负整数mm:
f(xk+δmrk)≤f(xk)+σδm(gk)Tdk
5.令αk=δ^mk,xk=xk+1=αk*dk,k=k+1并转向2
2.matlab程序
代码如下(示例):
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%用 阻尼牛顿法 求单变量函数在单峰区间[a,b]上的近似极小点
%在命令窗口输入函数: [newx,newfk,k]=QNewton('fun','gfun','Hess',xk)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function [newx,newfk,k]=QNewton(fun,gfun,Hess,xk)
%功能: 阻尼牛顿法 Armijo法非精确线搜索
%输入: xk是初始点,fun是目标函数, gfun是目标函数的梯度,Hess是Hesse矩阵的函数
%输出: newx, newfk分别是近似极小点和极小值
% k表示迭代次数
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
maxk=5000;
rho=0.5; % rho取值范围为[0,0.5]
sigma=0.4; % sigma取值范围为[rho,1]
k=0;
epsilon=1e-5;
while(k<=maxk)
gk=feval(gfun,xk);
Gk=feval(Hess,xk);
dk=-Gk\gk; % 解方程Gk*dk=-gk,计算搜索方向
if(norm(dk)<epsilon) break; end % 检验终止准则
m=0; mk=0;
while(m<20) % Armijo法非精确线搜索
if (feval(fun,xk+rho^m*dk) <= feval(fun,xk)+sigma*rho^m*gk'*dk)
mk=m; break;
end
m=m+1;
end
xk=xk+rho^mk*dk;
k=k+1;
end
newx=xk;
newfk=feval(fun,newx);
function f=fun(x)
f=4*x(1)^2+x(2)^2-8*x(1)-4*x(2);
function gf=gfun(x)
gf=[8*x(1)-8;
2*x(2)-4];
function He=Hess(x)
n=length(x);
He=zeros(n,n);
He=[8 0;0 2]
总结
[newx,newfk,k]=QNewton('fun','gfun','Hess',[0 0]')
He =
8 0
0 2
newx =
1
2
newfk =
-8
k =
1