图是一种比较复杂的数据结构,设计图的算法有很多,如图的搜索,最短路径,最小生成树等,这篇博客主要和大家讨论图的定义和如何去表示,相信看完本篇之后,也会对图有一个基本的了解。
图的定义
之前我们讨论过树,树是一种非线性表,今天所讨论的图也是一种非线性表。不过和树相比,图更加的复杂。树中的元素称为节点,对应的,图中的元素称为顶点(vertex)。图中的一个定点可以与任意其他顶点建立连接关系,我们把这种关系称为边(edge)。
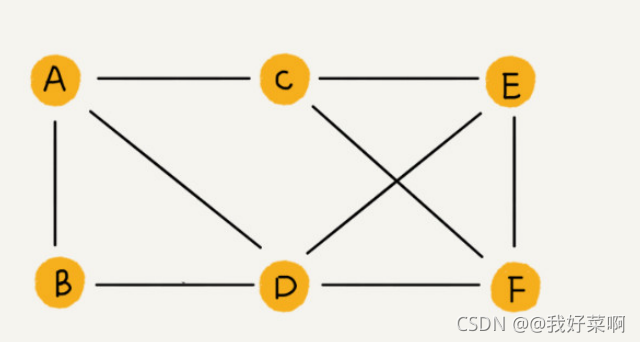
其实在我们生活中,就有很多符合图这种结构的例子。例如,我们的社交网络就是一个非常典型的图结构。就比如说我们用的微信,我们可以把每个用户看成一个顶点,如果两个用户互相加好友,就在对应的两个节点之间建立一条边。因此,微信的整个好友关系可以用一张图来进行表示。其中,每个用户有多少好友,对应的图中,就称为顶点的度(degree),也就是与顶点相连接的边的条数。
可以微博大家都知道,他的社交关系和微信又有些不同。微博允许单向关注,也就是说,用户A可能关注了用户B,但是用户B没有关注用户A,那么这种单向的社交关系,又该如何表示呢?
我们可以将图中的边,引入“方向”这个概念。如果用户A关注了用户B,那么就从图中画一条从A指向B的箭头,如果互相关注,那么我们就画两条边。我们把这种有方向的图称为有向图,相反,没有方向的就称为无向图。
 ?
?
无向图中顶点的“度”表示此顶点有多少条边与其相连。在有向图中,我们把度分为入度(in-degree)和出度(out-degree)。
顶点的入度,表示有多少条边指向这个顶点;顶点的出度,是指有多少条边是以这个顶点为起点指向其他的顶点。对应这个例子,就是微博中的粉丝量,入度表示有多少粉丝,出度就是你关注了哪些人。
现在再来看另一个社交软件QQ,QQ与微信相比,功能更加的复杂,大家可能关注到过亲密度这个功能。那么对应到图中,这个图就叫做带权图(weighted graph)。在带权图中,每条边都有一个权重(weight),我们用权重来表示QQ好友间的亲密度。
 ?
?
邻接矩阵的存储方法
知道了图的基本概念,我们就再来看看内存中如何存储图这种数据结构。
图最直观的一种存储方式为邻接矩阵(adjacency matrix)。学过线性代数的同学,应该都知道矩阵这个概念。邻接矩阵底层依赖二维数组。对于无向图来说,如果顶点i和顶点j之间有边,我们就将A[i][j]和A[j][i]标记为1;对于有向图,如果有一条从顶点i指向顶点j的边,我们就将A[i][j]标记为1,同理,如果有一条从顶点j指向顶点i的边,我们就将A[j][i]标记为1。对于带权图,数组中存储相应的权重。
 ?
?
现在来看看代码实现
public class Graph{
private int v;
private boolean matrix[][];
public Graph(int v){
this.v = v;
matrix = new boolean[v][v];
for(int i = 0;i < v;i++){
for(int j = 0;j < v;j++){
matrix[i][j] = false;
}
}
}
public void addEdge(int s,int t){
//无向图
matrix[s][t] = true;
matrix[t][s] = true;
}
}?因为邻接矩阵底层依赖数组,所以,在邻接矩阵中,获取两个顶点之间的关系的操作相当。这种存储的另一个好处就是可以把图中的很多运算转换为矩阵运算,方便计算。
邻接表的存储方法
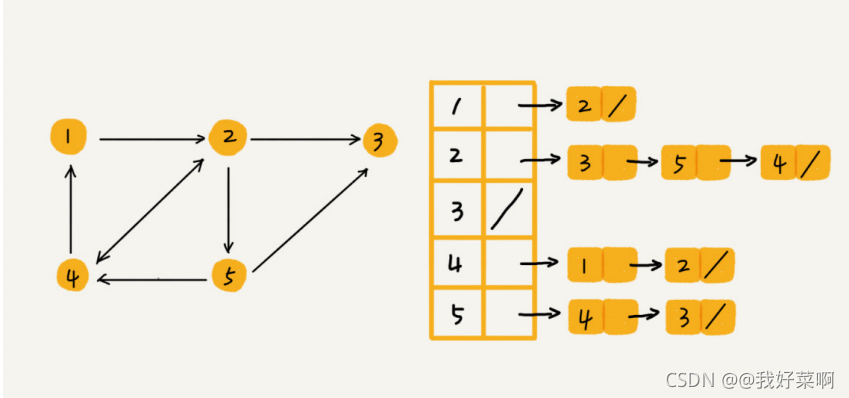
接下来用代码实现一下
public class Graph{
private int v;
private LinkedList<Integer>[] adj;//邻接表
public Graph(int v){
this.v = v;
adj = new LinkedList<>[v];
for(int i = 0;i < v;i++){
adj[i] = new LinkedList<>[];
}
}
public vid addEdge(int s,int t){
//无向图的一条边存储两次
adj[s].add[t];
adj[t].add[s];
}
}?之前我们还讨论过时间复杂度和空间复杂度互换的设计思想。邻接矩阵存储起来比较浪费空间,但是使用起来比较高效。相反,邻接表存储起来比较节省空间,但是使用起来就没有那么高效。
在之前讨论哈希表的时候,我们就提到过,基于链表法解决冲突的哈希表,对于链表过长,我们可以将链表转换为红黑树。
聊一聊别的
有了对于堆的基础知识,那我们来看看微博,微信等社交网络中的好友关系是如何存储的。
前面我们讨论到,微博,微信用的是两种不同的图,前者是有向图,后者是无向图,但是在解决思路上,确实差不多,下面先看看微博来进行举例。
针对微博的用户关系,我们假设需要支持下面几个操作。
 ?
?
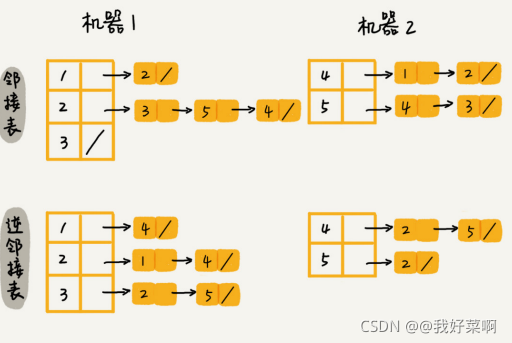
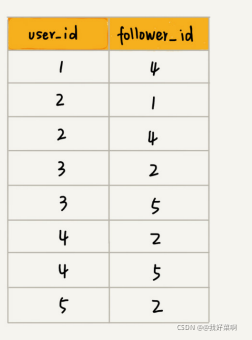
如上图,邻接表中存储了用户的关注关系,逆邻接表中存储用户的被关注关系。对应到图上,在邻接表中,每个顶点对应的链表存储这个顶点指向的顶点;在逆邻接表中,每个顶点对应的链表存储指向这个顶点的顶点。在邻接表中查找某个用户关注了哪些用户,在逆邻接表中查找某个用户被哪些用户关注。
基础的邻接表不适合判断两个用户之间是否关注与被关注的关系,因此我们将邻接表中的链表改改为支持快速查找的动态数据结构,但是选择哪种动态数据结构,又是一个问题?红黑树,跳表,有序动态数组还是哈希表呢?
?
?
?