文章目录
Leetcode84
1.问题描述

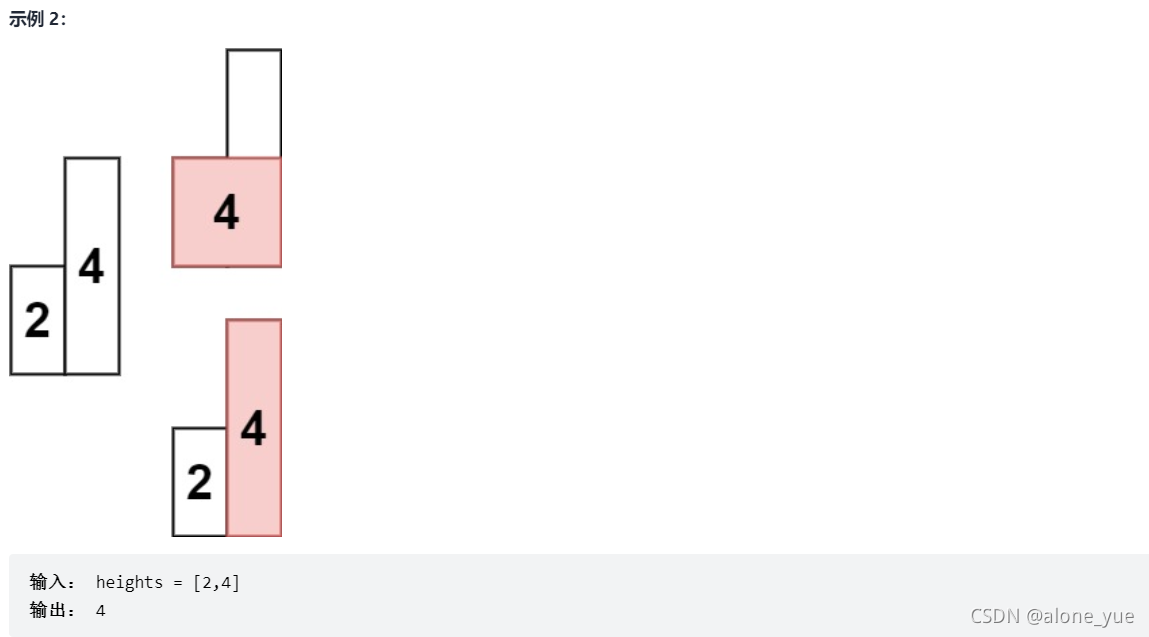
2.解决方案
解法一:双指针(O(n^2)超时)(想问题解决方案的思考!!!!!!)
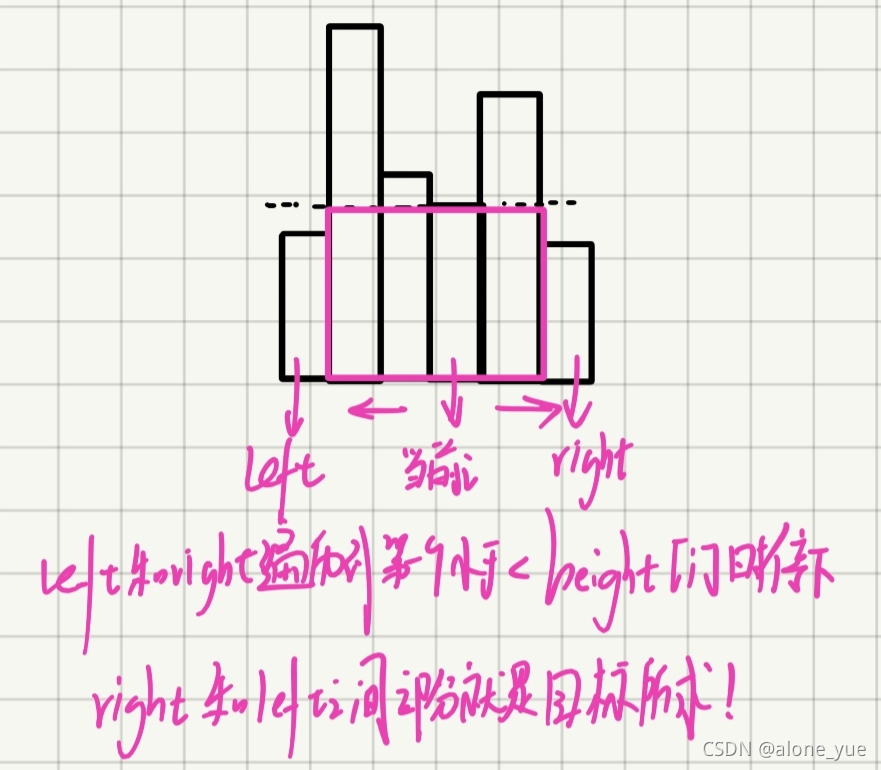
1.一看图基本就懂了,对于每一个柱子,包含这个柱子最大的矩形就是,左右第一比它小的柱子之间的区域,然后没一根柱子再求最大值,一定能保证找到答案
2.说实话能想到这个程度,虽然双指针没过,但题已经基本解决了,就是分别找左右第一个比它小的数
3.(想问题解决方案的思考!!!!!!)那么怎么能想到这一步呢,题目给的样例都不是很普遍,我们想要归纳或者说看出来必须自己举例子,比如你看到题目的样例都是左小右大,那你为什么不想一想,凹槽或者突起的最大值分别是什么样子的,把一边大一边小,凹槽突起都举例子看一下,你就能归纳出来了,奥原来找到两边第一个小的数,中间就是包含当前柱子的最大值!!!!!
class Solution {
public:
int largestRectangleArea(vector<int>& heights) {
int Max=-1;
for(int i=0;i<heights.size();i++){
int left=i-1;
int right=i+1;
for(;left>=0;left--){
if(heights[left]<heights[i]) break;
}
for(;right<heights.size();right++){
if(heights[right]<heights[i]) break;
}
Max=max(Max,(right-left-1)*heights[i]);
}
return Max;
}
};
解法二:动态规划(跳跃式节省计算的思路十分值得借鉴!!!!!)
思路与思考:
1.和上一题【Leetcode单调栈】42. 接雨水(有dp优化双指针计算!!双指针,动态规划,单调栈!!)的dp优化双指针如出一辙,但是上一题的dp比较常规,本题稍微有一点技巧,上一题记录值,本题记录下标index,但都是节省计算!
2.本题的dp是通过之前记录过的右边第一个小的下标index,然后跳跃着比较,一些中间值是肯定大于height[i]的就不用比较了,图片已经说的很清楚了
3.这种跳跃式节省计算的思路十分值得借鉴!!!!!

代码实现:
1.代码实现初始化要注意,这个初始化很有用,推一下i==1的情况就会发现必须初始化为-1和heights.size()否则会死循环,并且实际意义也有,-1或者height.size(),就代表左边或右边没有比自己小的,求区间长度也是刚好符合条件
2.就是遇见相同的元素还得往前找,随便举个例子就懂了!
//while(t>=0&&heights[t]>heights[i]) t=leftFirstMin[t];
while(t>=0&&heights[t]>=heights[i]) t=leftFirstMin[t];
class Solution1 {
public:
int largestRectangleArea(vector<int>& heights) {
//1.[0,本身)左边第一个小的index (本身,heights.zie()]右边第一个小的index
//这个初始化很有用,推一下i==1的情况就会发现必须初始化为-1和heights.size()否则会死循环
//并且实际意义也有,-1或者height.size(),就代表左边或右边没有比自己小的,求区间长度也是刚好符合条件
vector<int> leftFirstMin(heights.size(),-1);
vector<int> rightFirstMin(heights.size(),heights.size());
//2.
for(int i=1;i<heights.size();i++){
int t=i-1;
//while(t>=0&&heights[t]>heights[i]) t=leftFirstMin[t];
while(t>=0&&heights[t]>=heights[i]) t=leftFirstMin[t];
leftFirstMin[i]=t;
}
for(int i=heights.size()-2;i>=0;i--){
int t=i+1;
//while(t<=heights.size()-1&&heights[t]>heights[i]) t=rightFirstMin[t];
while(t<=heights.size()-1&&heights[t]>=heights[i]) t=rightFirstMin[t];
rightFirstMin[i]=t;
}
//3.
int Max=-1;
for(int i=0;i<heights.size();i++){
Max=max(Max,heights[i]*(rightFirstMin[i]-leftFirstMin[i]-1));
}
return Max;
}
};
解法三:单调栈
思考:
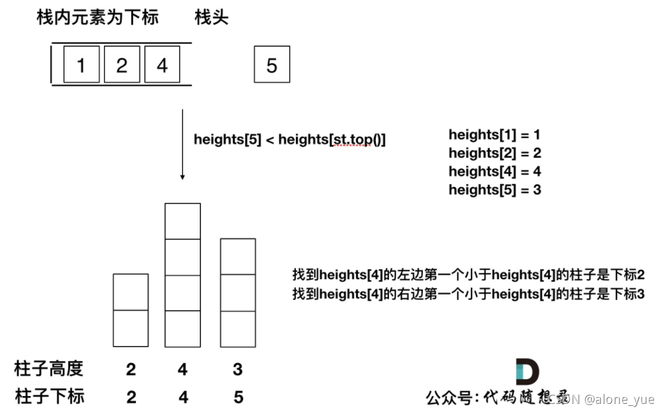
1.【Leetcode单调栈】42. 接雨水(有dp优化双指针计算!!双指针,动态规划,单调栈!!)是找每个柱子左右两边第一个大于该柱子高度的柱子,而本题是找每个柱子左右两边第一个小于该柱子的柱子。
2.这里就涉及到了单调栈很重要的性质,就是单调栈里的顺序,是从小到大还是从大到小。 在【Leetcode单调栈】42. 接雨水(有dp优化双指针计算!!双指针,动态规划,单调栈!!)中我讲解了接雨水的单调栈从栈头(元素从栈头弹出)到栈底的顺序应该是从小到大的顺序。那么因为本题是要找每个柱子左右两边第一个小于该柱子的柱子,所以从栈头(元素从栈头弹出)到栈底的顺序应该是从大到小的顺序!
3.栈顶和栈顶的下一个元素以及要入栈的三个元素组成了我们要求最大面积的高度和宽度,其实就是一个凸就是我们要求的最大面积!(当初想这个凸怎么想出来的上面双指针法有反思总结!!)
代码实现一:二次检查
1.代码实现就三张情况搞清楚就好了,老生常谈了属于是,其中第三种还是注意,left和right的值,就是对一个凸求最大面积。
2.有一种情况就是最后剩下一个递增序列,也就是右边没有比他们小的了一直递增,1,2,4,5,6…,那么这种情况其实就时再检查一遍就好,一样left和right要想清楚了!!
class Solution2 {
public:
int largestRectangleArea(vector<int>& heights) {
//递增栈↑
stack<int> stack;
//构建单调栈
stack.push(0);
int Max=-1;
for(int i=1;i<heights.size();i++){
//1.
if(heights[stack.top()]<heights[i]){
stack.push(i);
continue;
}
//2.
if(heights[stack.top()]==heights[i]){
stack.push(i);
continue;
}
//3.
if(heights[stack.top()]>heights[i]){
while(stack.empty()== false&&heights[stack.top()]>heights[i]){
int mid=stack.top(); stack.pop();
int left;
int right=i;
if(stack.empty()== false) left=stack.top();
else left=-1;
Max=max(Max,heights[mid]*(right-left-1));
}
stack.push(i);
}
}
//如果栈未空,证明里面还有递增序列,相当于这几个值右边没有比他们小的了
//那right=height.size()就对了
//left就是栈中前一个元素呗刚好
while(stack.empty()== false){
int mid=stack.top(); stack.pop();
int left;
int right=heights.size();
if(stack.empty()== false) left=stack.top();
else left=-1;
Max=max(Max,heights[mid]*(right-left-1));
}
return Max;
}
};
代码实现二:首尾插入0避免二次检查
首尾插入0,这个一般想不到就记一下就好了,分析一下确实加了0就会把剩余的递增序列都清空的而且left和right也恰到好处,秒啊!
class Solution3 {
public:
int largestRectangleArea(vector<int>& heights) {
//递增栈↑
stack<int> stack;
heights.insert(heights.begin(),0); //-----改变1
heights.push_back(0);
//构建单调栈
stack.push(0);
int Max=0; //int Max=-1; //-----改变2
for(int i=1;i<heights.size();i++){
//1.情况1
if(heights[stack.top()]<heights[i]){
stack.push(i);
continue;
}
//2.情况2
if(heights[stack.top()]==heights[i]){
stack.push(i);
continue;
}
//3.情况3
if(heights[stack.top()]>heights[i]){
while(stack.empty()== false&&heights[stack.top()]>heights[i]){
int mid=stack.top(); stack.pop();
int left;
int right=i;
if(stack.empty()== false) left=stack.top();
else left=-1;
Max=max(Max,heights[mid]*(right-left-1));
}
stack.push(i);
}
}
//-----改变3
如果栈未空,证明里面还有递增序列,相当于这几个值右边没有比他们小的了
那right=height.size()就对了
left就是栈中前一个元素呗刚好
//while(stack.empty()== false){
// int mid=stack.top(); stack.pop();
// int left;
// int right=heights.size();
// if(stack.empty()== false) left=stack.top();
// else left=-1;
// Max=max(Max,heights[mid]*(right-left-1));
//}
return Max;
}
};