每日一练
10.1
- 判断下列说法是否正确:内部排序方法的稳定性是指该排序算法不允许有相同的关键字记录。
A. 正确
B. 错误
【答案】B
10.2
- 下面有关JVM内存,说法错误的是?
A. 程序计数器是一个比较小的内存区域,用于指示当前线程所执行的字节码执行到了第几行,是线程隔离的
B. 虚拟机栈描述的是Java方法执行的内存模型,用于存储局部变量,操作数栈,动态链接,方法出口等信息,是线程隔离的
C. 方法区用于存储JVM加载的类信息、常量、静态变量、以及编译器编译后的代码等数据,是线程隔离的
D. 原则上讲,所有的对象都在堆区上分配内存,是线程之间共享的
【答案】C
10.3
- 下面有关jdbc statement的说法错误的是?
A. JDBC提供了Statement、PreparedStatement 和 CallableStatement三种方式来执行查询语句,其中 Statement 用于通用查询, PreparedStatement 用于执行参数化查询,而 CallableStatement则是用于存储过程
B. 对于PreparedStatement来说,数据库可以使用已经编译过及定义好的执行计划,由于 PreparedStatement 对象已预编译过,所以其执行速度要快于 Statement 对象”
C. PreparedStatement中,“?” 叫做占位符,一个占位符可以有一个或者多个值
D. PreparedStatement可以阻止常见的SQL注入式攻击
【答案】C
10.4
- 已知数据表A中每个元素距其最终位置不远,为节省时间排序,应采用什么方法排序?
A. 堆排序
B. 插入排序
C. 快速排序
D. 直接选择排序
【答案】B
10.5
- 以下哪种操作最适合先进行排序处理?
A. 找最大最小值
B. 计算平均值
C. 找中位数
D. 找出现次数最多的值
【答案】C
10.6
- 下列排序算法中,元素的移动次数与关键字的初始排列次序无关的是 。
A. 直接插入排序
B. 冒泡排序
C. 基数排序
D. 快速排序
【答案】C
10.7
- 判断下列说法是否正确:二叉排序树上结点的关键字的值有可能相同。()
A. 正确
B. 错误
【答案】B
10.8
- 设有序顺序表中有n个数据元素,则利用二分查找法查找数据元素X的最多比较次数不超过()。
A. lgn+1
B. lgn-1
C. lgn
D. lg(n+1)
【答案】D
10.9
- 下面有关SPRING的事务传播特性,说法错误的是?
A. PROPAGATION_SUPPORTS:支持当前事务,如果当前没有事务,就以非事务方式执行
B. PROPAGATION_REQUIRED:支持当前事务,如果当前没有事务,就抛出异常
C. PROPAGATION_REQUIRES_NEW:新建事务,如果当前存在事务,把当前事务挂起
D. PROPAGATION_NESTED:支持当前事务,新增Savepoint点,与当前事务同步提交或回滚
【答案】B
10.10
- 下面有关servlet和cgi的描述,说法错误的是?
A. servlet处于服务器进程中,它通过多线程方式运行其service方法
B. CGI对每个请求都产生新的进程,服务完成后就销毁
C. servlet在易用性上强于cgi,它提供了大量的实用工具例程,例如自动地解析和解码HTML表单数据、读取和设置HTTP头、处理Cookie、跟踪会话状态等
D. cgi在移植性上高于servlet,几乎所有的主流服务器都直接或通过插件支持cgi
【答案】D
10.11
-
对一棵空的字典树依次插入如下单词后,字典树中节点个数为()。
① aba
② abb
③ abc
④ bac
⑤ bad
⑥ bdc
A. 11
B. 12
C. 15
D. 16
【答案】B
【解析】最终的字典树如下所示
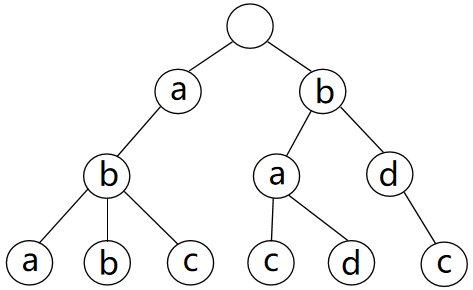
10.12
-
下列关于字典树的叙述中,正确的是()。
① 字典树又称trie树,1981年ACM协会对此数据结构命名以纪念计算机科学先驱Bananaoa Trie
② 向字典树中插入一个长度为n的字符串的时间复杂度为O(n)
③ 字典树本质上是一个确定有限状态自动机(DFA)
A. 仅②
B. 仅 ①、②
C. 仅 ②、③
D. 仅 ①、③
【答案】C
【解析】字典树又称trie,这个术语来自于retrieval。trie的发明者是Edward Fredkin。字典树插入与查找的效率都取决于字符串长度,字典树本质上是一个确定有限状态自动机(DFA)。
10.13
- 对一个存放比特串(串中只包含0或1)的字典树进行m次插入操作,每次插入操作会往字典树中插入一个长度为n的比特串,其算法空间复杂度是()。
A. O(n·m)
B. O(n·2^m)
C. O(min(n·2m, m·2n))
D. O(min(n·m,2n))
【答案】D
【解析】当m远小于2n时,空间复杂度接近于n·m;当m接近或者超过2n时,此字典树深度为i的节点最多有2i个(设根节点深度为0),于是字典树中最多有20+21+…+2n=2n+1-1。