我们在学习数学和编程的时候总会听到一个叫杨辉三角的东西。首先介绍什么是杨辉三角？
杨辉三角，是二项式系数在三角形中的一种几何排列，中国南宋数学家杨辉1261年所著的《详解九章算法》一书中出现。在欧洲，帕斯卡（1623----1662）在1654年发现这一规律，所以这个表又叫做帕斯卡三角形。帕斯卡的发现比杨辉要迟393年，比贾宪迟600年。引自百度百科
为祖先的智慧点赞！！
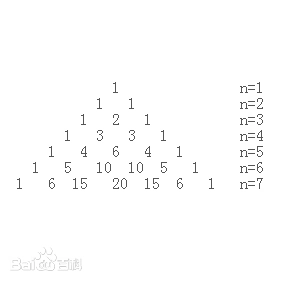
通俗的讲，杨辉三角就是个由数字组成的三角形，三角形的顶是1，三角形的两个侧边也全是1，第几行就存在几个数字。通过观察每一行数字，我们可以发现，出来侧边上数字之外，每个数都是上面两个数字的和。
通过下面一个表来形象的观察，除去侧边，我们来观察橘红色的部分，可以看到每个数都是它上面两个数的和。
到这里，我们已经了解了什么是杨辉三角了，对杨辉三角的一些特性（编写程序时会用到）也基本掌握了。接下来，让我们用代码实现它。代码使用Java语言，使用二维数组和递归两种方式实现。
输出形式
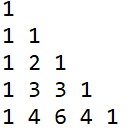
1. 二维数组
这是比较简单好理解的一种方式。首先，我们将杨辉三角想象成一个二维数组a[i][i]，对于侧边总是1的情况分析，左边侧边就是a[i][0]，即当我们的j=0的时候数组值应该是1；同理当为==a[i][j]==中的i=j的时候，为右边上的数字，此时数组的值也为1。如下：
if (j==0 || j==i) {
a[i][j] = 1;
}
对于除去侧边的其它数字的数值是它上面的两个数的和，用数组表示就是
a[i][j] = a[i-1][j] + a[i-1][j-1]
到这里我们对如何使用二维数组表示杨辉三角里面的数字已经很清楚。
全部代码如下：
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
//定义一个数n作为杨辉三角的行数
int n = scanner.nextInt();
/*
* 根据n构建空的二维数组
* 一共n行，一行n个数
*/
int a[][] = new int[n][n] ;
//循环n行
for (int i = 0; i <n; i++) {
//每行有n个数字
for (int j = 0; j <= i; j++) {
//如果是这一行第一个或者最后一个数，设置为1，并存入数组
if (j==0 || j==i) {
a[i][j] = 1;
//否则，该数为上面两数之和，存入二维数组
}else {
a[i][j] = a[i-1][j] + a[i-1][j-1];
}
//输出数字
System.out.print(a[i][j]+" ");
}
//换下一行
System.out.println();
}
}
输入：4
输出：
1
1 1
1 2 1
1 3 3 1
2. 使用递归
使用递归的思想就是构造一个递归函数fun(int i,int j)，传入两个参数分别作为行和列，如果是第一列（j=0）或者最后一列（j=i）则返回1，否则这个数等于上一行的两个数的和，同数组原理差不多：fun(i-1, j) + fun(i-1, j-1)。
//构建递归函数，参数i表示行，j表示列
static private int fun(int i,int j) {
//判断是否是该行第一个数或者最后一个，如果是返回1
if (j==1||i==j) {
return 1;
//否则是上一行上面两数之和
}else {
return fun(i-1, j) + fun(i-1, j-1);
}
}
public static void main(String[] args) {
//定义一个数n作为杨辉三角的行数
int n;
Scanner scanner = new Scanner(System.in);
n = scanner.nextInt();
//此循环是行数
for (int i = 1; i <= n; i++) {
//此循环是列数
for (int j = 1; j <= i; j++) {
//调用构造函数打印即可
System.out.print(fun(i, j)+" ");
}
//换行
System.out.println();
}
}
输入：4
输出：
1
1 1
1 2 1
1 3 3 1
菜鸡冲冲冲！！1