题意
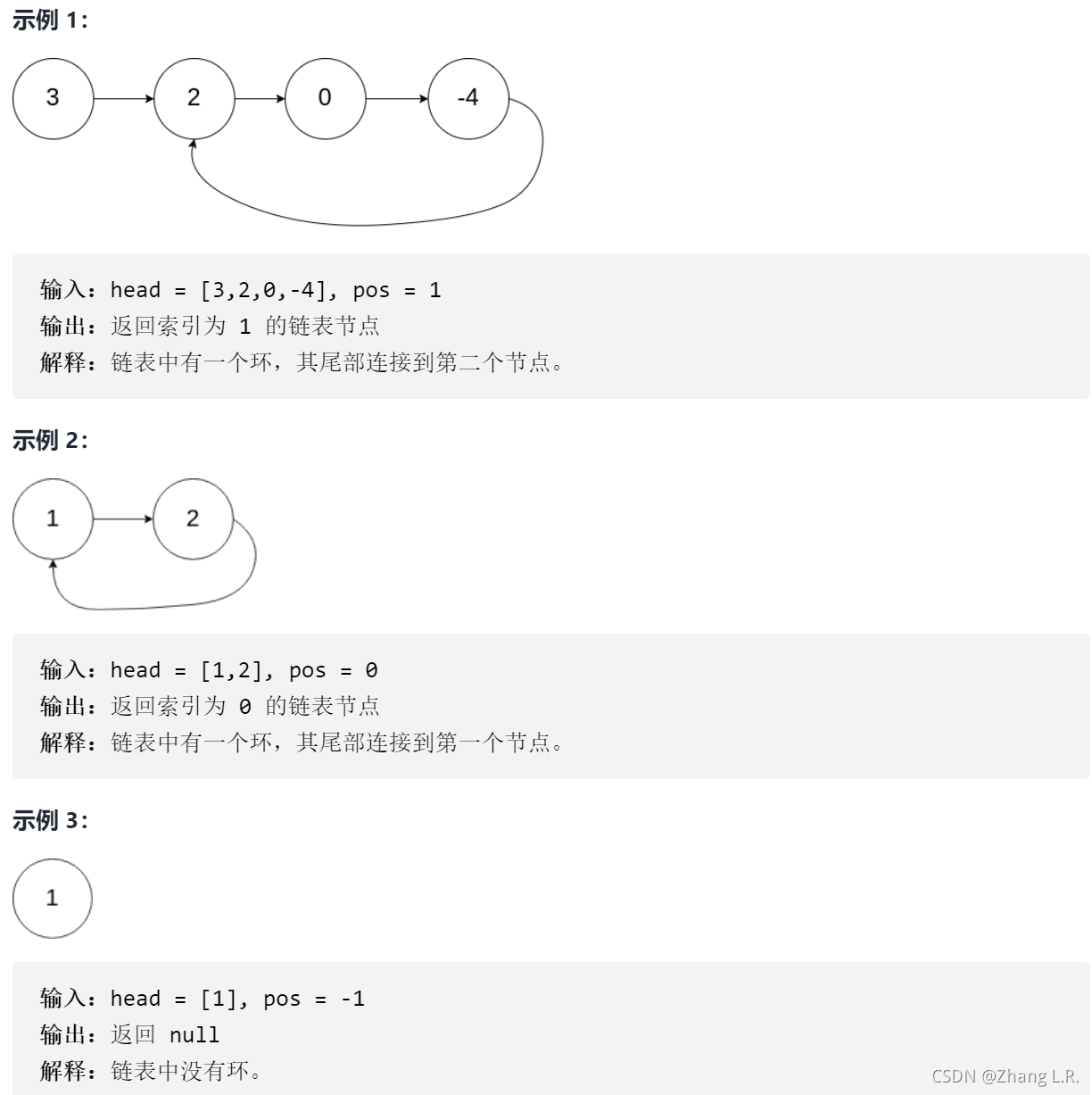
给定一个链表,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。
解题思路
① 设双指针
f
a
s
t
fast
fast 和
s
l
o
w
slow
slow ,其中
f
a
s
t
fast
fast 每次前进2步、
s
l
o
w
slow
slow每次前进1步。如果
f
a
s
t
fast
fast 最终为NULL,那么该链表无环;反之,
f
a
s
t
fast
fast 和
s
l
o
w
slow
slow必会在某一点相遇。
② 设
f
a
s
t
fast
fast 和
s
l
o
w
slow
slow相遇的点为
P
P
P,那么
s
l
o
w
slow
slow从
P
P
P点开始,
f
a
s
t
fast
fast从起始点,两个指针同时每次都前进一步,那两者最终相遇的地方即链表入环的第一个节点。
代码
/**
* 给定一个链表,如果有环路,找出环路的开始点。
*
* @author ZhangLingRan
*/
class ListNode {
int val;
ListNode next;
ListNode(int x) {
val = x;
next = null;
}
}
/**
* @author ZhangLingRan
*/
public class Solution{
public ListNode detectCycle(ListNode head) {
ListNode fast = head, slow = head;
while (fast != null && fast.next != null) {
fast = fast.next.next;
slow = slow.next;
if (fast == slow) {
break;
}
}
// 如果fast走到头,说明没环,那么返回NULL
if (fast == null || fast.next == null) {
return null;
}
//如果有环,那么找到第一次相遇的交点,slow从交点往后走、fast从head往后走,直到相遇即为交点
fast = head;
while (fast != slow) {
fast = fast.next;
slow = slow.next;
}
return fast;
}
}
方法证明
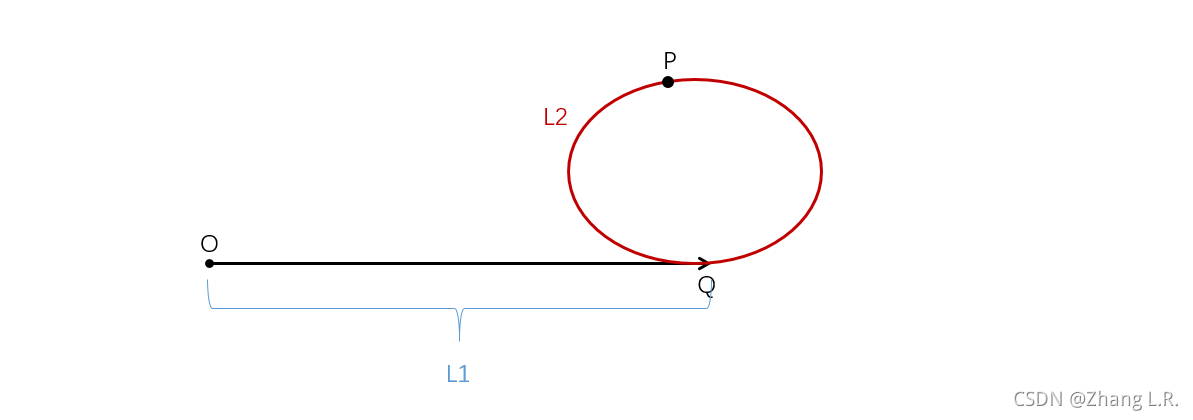
假设这是一个带有环的链表;其中
O
Q
OQ
OQ的长度为
L
1
L1
L1,环的长度为
L
2
L2
L2;两个指针在
P
P
P点相遇,那么当指针
s
l
o
w
slow
slow走到了
P
P
P点,其走过的路程为
∣
O
P
∣
=
L
1
+
∣
Q
P
∣
|OP| = L1+|QP|
∣OP∣=L1+∣QP∣,那么
f
a
s
t
fast
fast指针走过的路程为
2
∣
O
P
∣
=
L
1
+
L
2
+
∣
Q
P
∣
2|OP| = L1+L2+|QP|
2∣OP∣=L1+L2+∣QP∣。
由此可知:
2
∣
O
P
∣
=
L
1
+
L
2
+
∣
Q
P
∣
=
2
(
L
1
+
∣
Q
P
∣
)
2|OP| = L1+L2+|QP| = 2(L1+|QP|)
2∣OP∣=L1+L2+∣QP∣=2(L1+∣QP∣)
化简得
L
2
?
∣
Q
P
∣
=
L
1
,
即
∣
P
Q
∣
=
L
1
L2-|QP| = L1,即|PQ| = L1
L2?∣QP∣=L1,即∣PQ∣=L1
其中
∣
Q
P
∣
|QP|
∣QP∣表示从
Q
Q
Q点到
P
P
P点走过的路程,
∣
P
Q
∣
|PQ|
∣PQ∣表示从
P
P
P点到
Q
Q
Q的走过的路程。
由
∣
P
Q
∣
=
L
1
|PQ| = L1
∣PQ∣=L1可知,从
P
P
P点和
O
O
O点同时开始,每次前进一步,相遇点即链表的入环点。
-------------------我是分界线-----------------------
代码更新:
public ListNode detectCycle(ListNode head) {
ListNode fast = head, slow = head;
// 如果fast走到头,说明没环,那么返回NULL
do{
if (fast == null || fast.next == null) {
return null;
}
fast = fast.next.next;
slow = slow.next;
}while (fast != slow);
//如果有环,那么找到第一次相遇的交点,slow从交点往后走、fast从head往后走,直到相遇即为交点
fast = head;
while (fast != slow) {
fast = fast.next;
slow = slow.next;
}
return fast;
}