目录
题目:
用龙贝格算法计算下面积分:?
?
描述:
实际问题中对于难以计算的定积分,我们往往采用数值积分的方法实现,其中龙贝格求积公式就是一种 好用的数值积分算法,在龙贝格算法中,是在步长逐次分半的过程中,反复利用复化求积公式进行计算。
主要步骤:
1、二分次求得梯形值
2、外推法进一步提升精度
龙贝格算法公式:
实现代码:
#define _CRT_SECURE_NO_WARNINGS 1
#include <iostream>
#include <vector>
#include <cmath>
#include <string>
using namespace std;
//龙贝格算法计算 积分 I=0-1上x^3/2次方dx
class Romberg
{
public:
Romberg(int k,int a, int b, double e)
{
this->m_a = a;
this->m_b = b;
this->m_h = b - a;
this->m_k = k;
this->m_e = e;
double T0_0 = (pow(a, 1.5) + pow(b, 1.5)) * this->m_h / 2.0;
t.push_back(T0_0);
}
void getT0()
{
//double T0_1 = t[0] / 2.0 + this->m_h / 2.0 * pow(this->m_a + this->m_h / 2.0, 1.5);
for (int i = 1; i <= 5; i++)
{
double temp = 0;
for (int j = 1; j <= (int)pow(2,i-1); j++)
{
double num = this->m_a * 1.0 + (2.0*j-1.0) * (double)(this->m_h /pow(2,i));
temp += pow(num, 1.5);
}
double T0_i = t[i - 1] / 2.0 + this->m_h /pow(2,i-1) / 2.0 * temp;
t.push_back(T0_i);
//this->m_h /= 2.0;
}
}
void getT1()
{
for (int i = 1; i <= 5; i++)
{
double T1_i = pow(4, 1) * t[i] / (pow(4, 1) - 1.0) - t[i - 1] / (pow(4, 1) - 1);
t1.push_back(T1_i);
}
}
void getT2()
{
for (int i = 1; i <= 4; i++)
{
double T2_i = pow(4, 2) * t1[i] / (pow(4, 2) - 1.0) - t1[i - 1] / (pow(4, 2) - 1);
t2.push_back(T2_i);
}
}
void getT3()
{
for (int i = 1; i <= 3; i++)
{
double T3_i = pow(4, 3) * t2[i] / (pow(4, 3) - 1.0) - t2[i - 1] / (pow(4, 3) - 1);
t3.push_back(T3_i);
}
}
void getT4()
{
for (int i = 1; i <= 2; i++)
{
double T4_i = pow(4, 4) * t3[i] / (pow(4, 4) - 1.0) - t3[i - 1] / (pow(4, 4) - 1);
t4.push_back(T4_i);
}
}
void getT5()
{
for (int i = 1; i <= 1; i++)
{
double T5_i = pow(4, 5) * t4[i] / (pow(4, 5) - 1.0) - t4[i - 1] / (pow(4, 5) - 1);
t5.push_back(T5_i);
}
}
int m_k;
int m_h;
int m_a;
int m_b;
int m_e;
vector<double> t;
vector<double> t1;
vector<double> t2;
vector<double> t3;
vector<double> t4;
vector<double> t5;
};
int main()
{
Romberg r(0,0,1,0.0001);
r.getT0();
string T = "012345";
for (int i = 0; i < 6; i++)
{
cout << "T0_"<<T[i]<<" = " << r.t[i] << endl;
}
system("pause");
system("cls");
string T1 = "12345";
r.getT1();
cout << "-----------------------------------------------------" << endl;
cout << "加速一次" << endl;
for (int i = 1; i <= 5; i++)
{
cout << "T1_" << T1[i-1] << " = " << r.t1[i-1] << endl;
}
system("pause");
system("cls");
r.getT2();
string T2 = "1234";
cout << "-----------------------------------------------------" << endl;
cout << "加速二次" << endl;
for (int i = 1; i <= 4; i++)
{
cout << "T2_" << T2[i - 1] << " = " << r.t2[i - 1] << endl;
}
system("pause");
system("cls");
r.getT3();
cout << "-----------------------------------------------------" << endl;
cout << "加速三次" << endl;
for (int i = 1; i <= 3; i++)
{
cout << "T3_" << T[i - 1] << " = " << r.t3[i - 1] << endl;
}
system("pause");
system("cls");
r.getT4();
cout << "-----------------------------------------------------" << endl;
cout << "加速四次" << endl;
for (int i = 1; i <= 2; i++)
{
cout << "T4_" << T[i - 1] << " = " << r.t4[i - 1] << endl;
}
system("pause");
system("cls");
r.getT5();
cout << "-----------------------------------------------------" << endl;
cout << "加速五次" << endl;
for (int i = 1; i <= 1; i++)
{
cout << "T4_" << T[i - 1] << " = " << r.t5[i - 1] << endl;
}
system("pause");
system("cls");
return 0;
}运行结果:
梯形值:
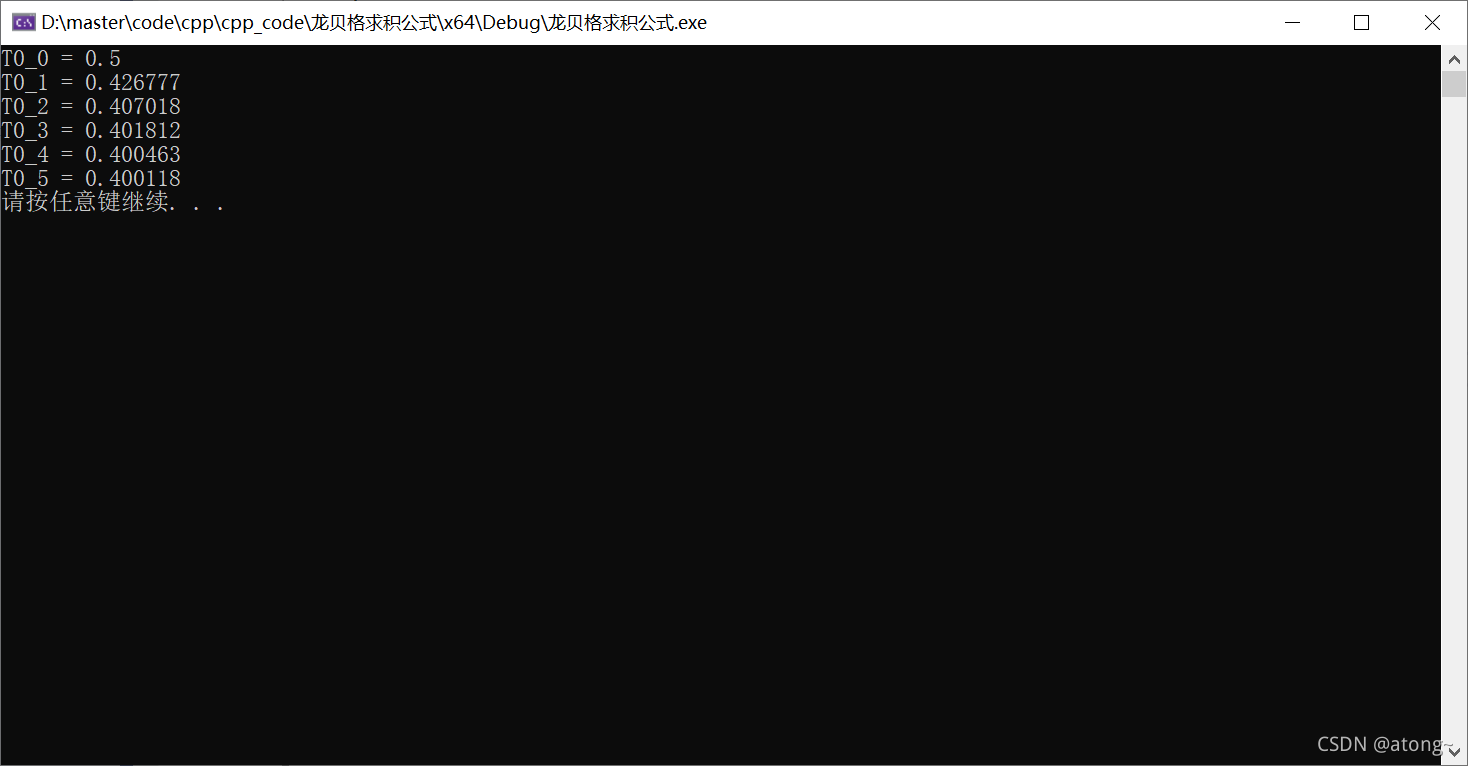
加速一次:
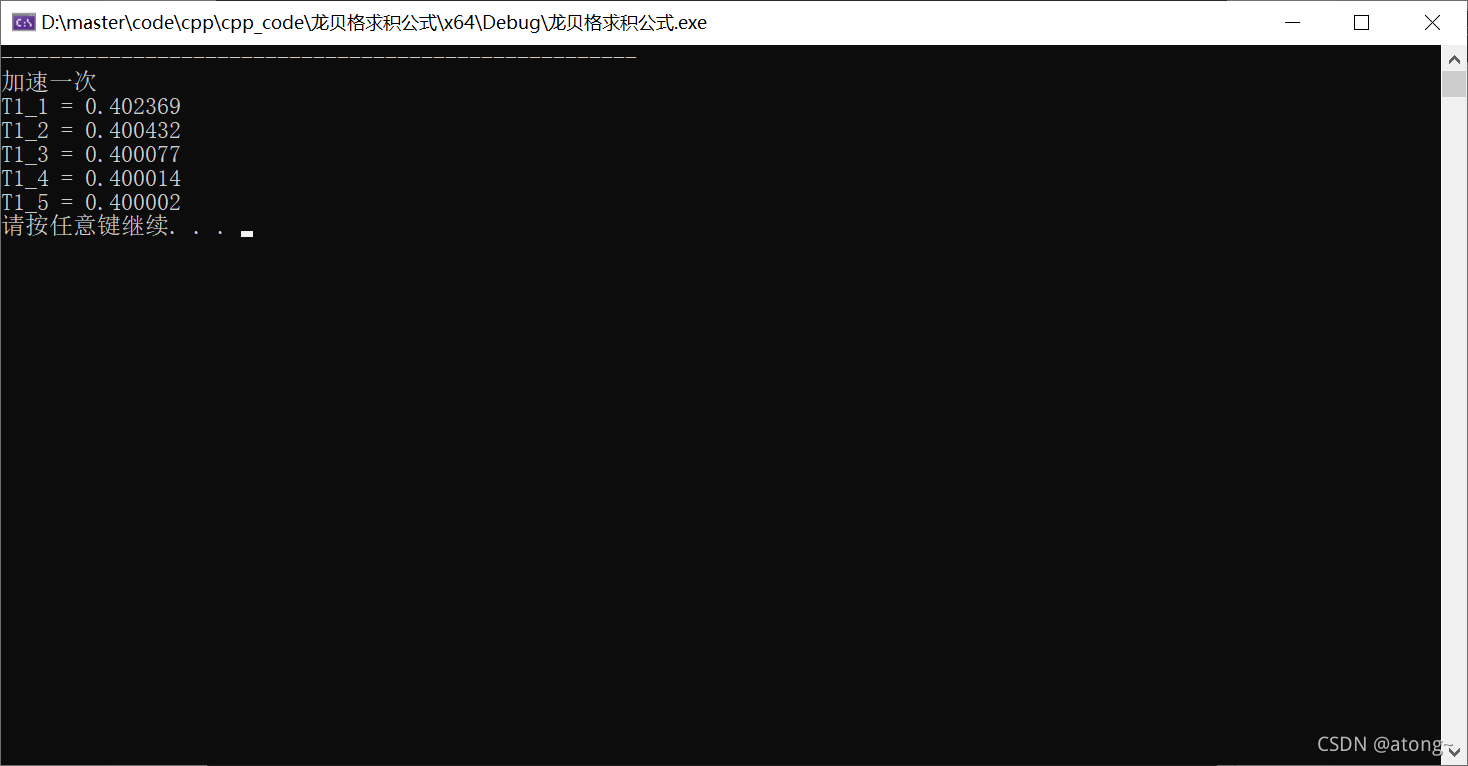
加速两次:
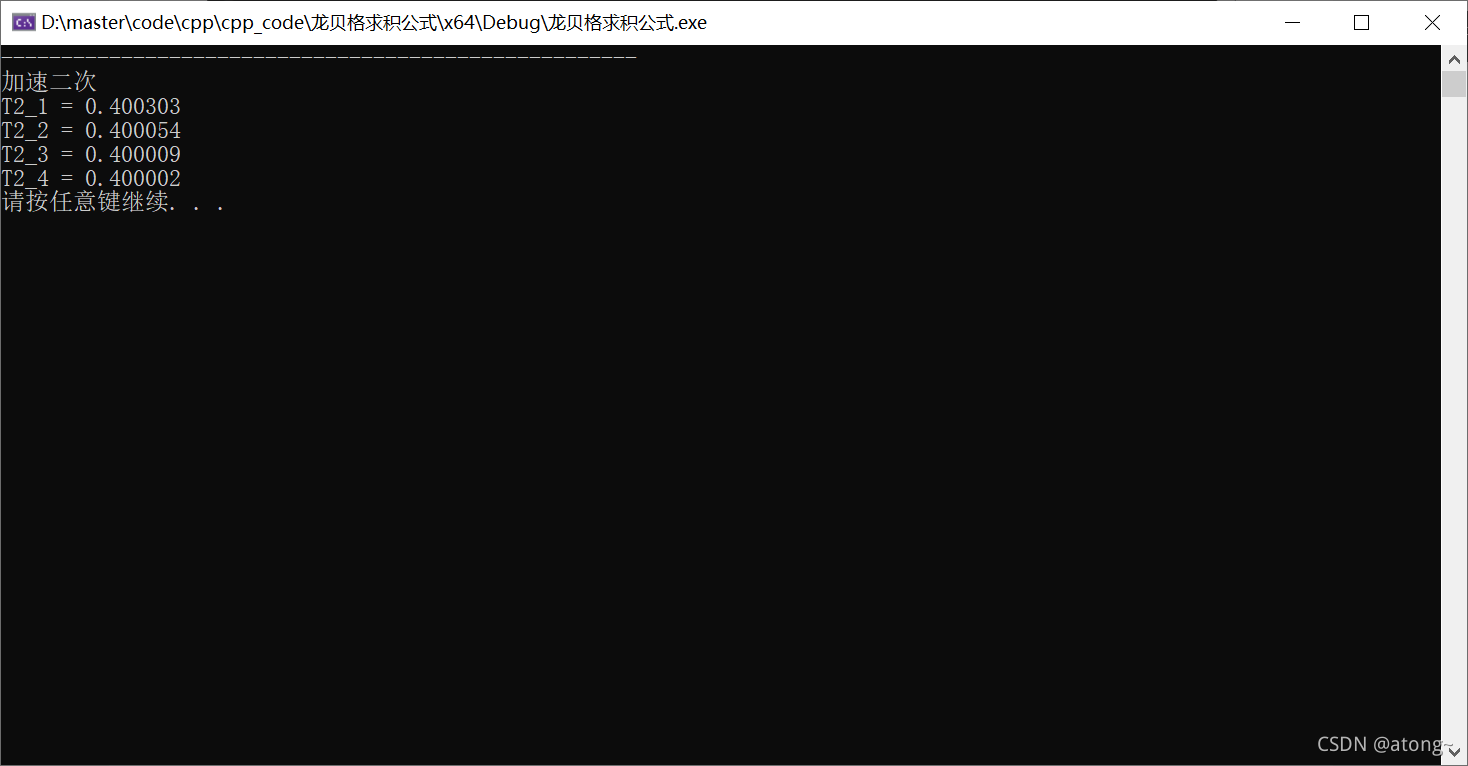
加速三次:
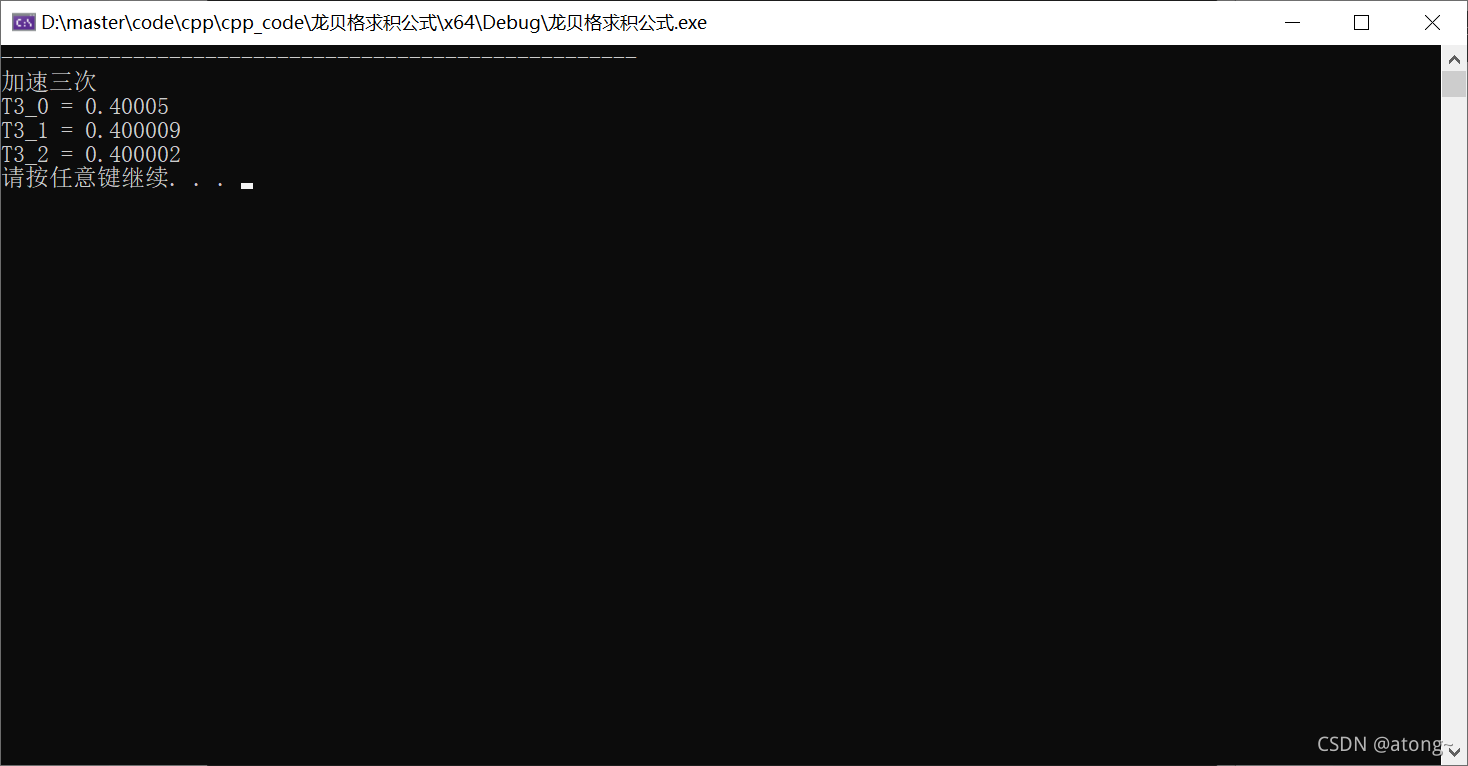
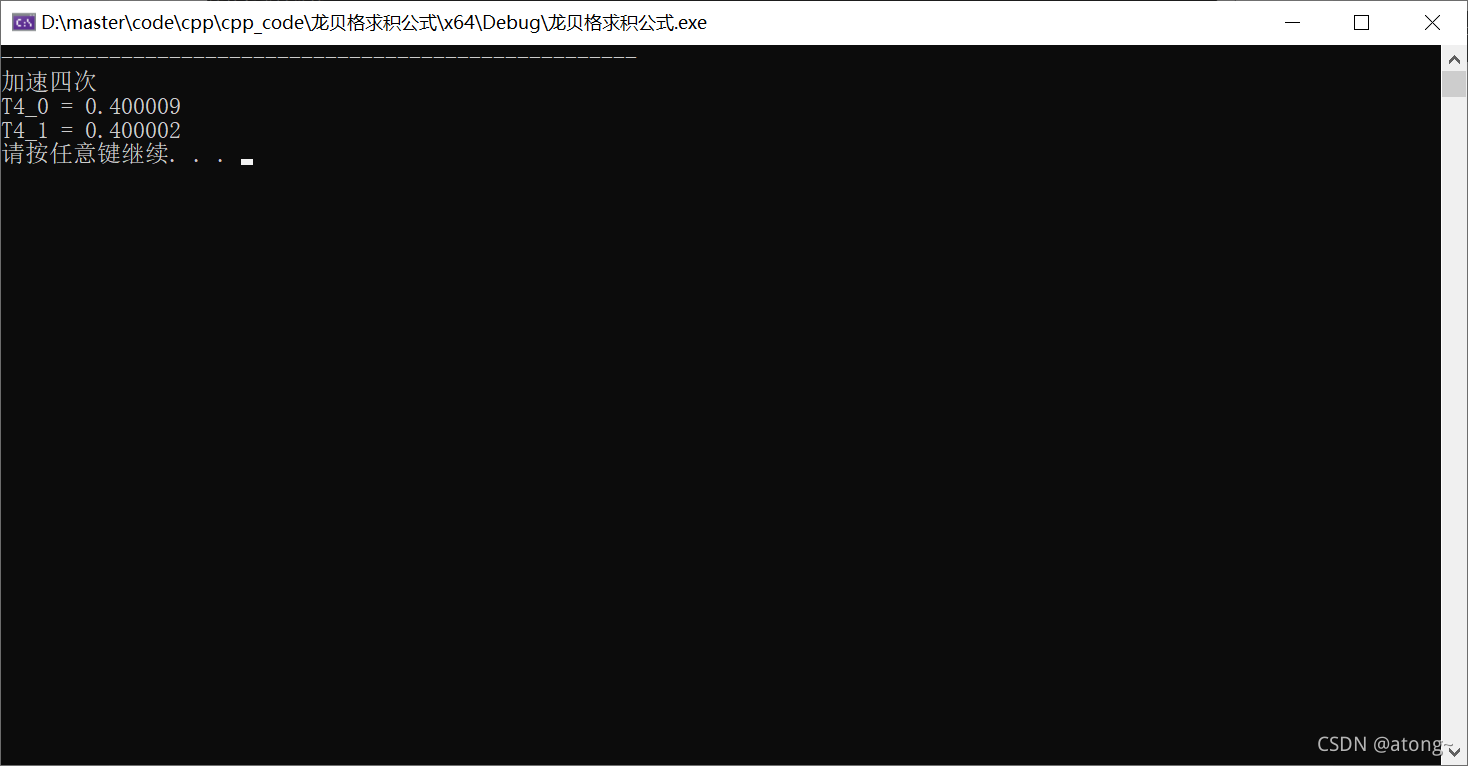
加速四次:?
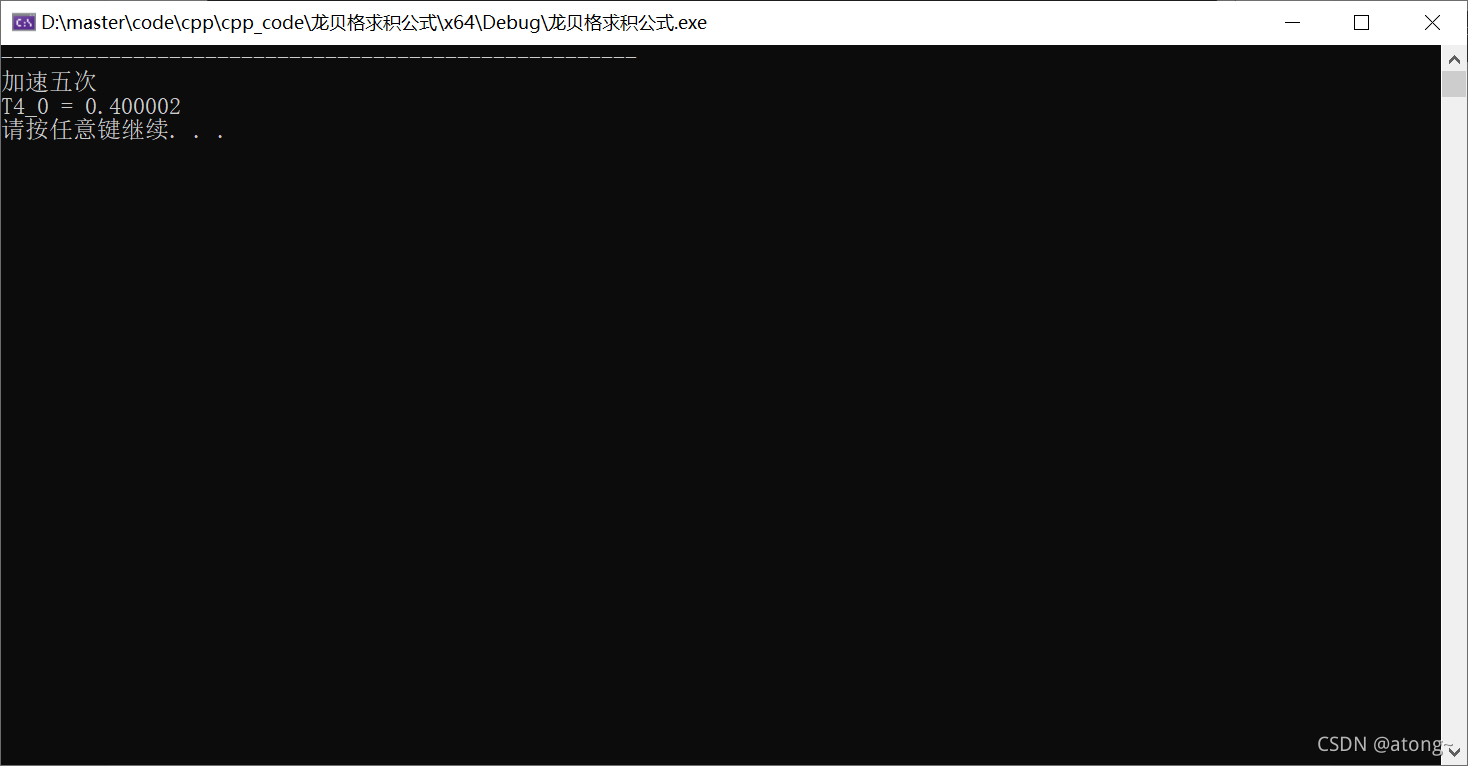
加速5次:
计算结果:
| k | ||||||
| 0 | 0.500000 | |||||
| 1 | 0.426777 | 0.402369 | ||||
| 2 | 0.407018 | 0.400432 | 0.400302 | |||
| 3 | 0.401812 | 0.400077 | 0.400054 | 0.400050 | ||
| 4 | 0.400463 | 0.400014 | 0.400009 | 0.400009 | 0.400009 | |
| 5 | 0.400118 | 0.400002 | 0.400002 | 0.400002 | 0.400002 | 0.400002 |
优化相关:
本文并未做程序优化,程序相当冗余并且,没啥普适性,优化建议如下:
1、加速值写成循环结构
2、根据预设精度判断二分次数
3、能不能把函数封装一下