??本文记录了一些有关树这种数据结构相对初阶的知识。
??如果你是已经有一定的树这种数据结构的基础想知道为什么研究树要重点研究二叉树,可以去看目录 13、树、森林与二叉树的转化;如果你是和我一样的小白想循序了解一些树的有关知识,可以从头看起。
文章目录
?1.树的定义
??树是n个节点的有限集。n=0时称为空树。在任意一颗非空树中:
- 有且仅有一个特定的称为根(Root)的结点;
- 当n>1时,其余结点可以分为m(m>0)个互不相交的有限集T1、T2、…、Tm,其中每个集合本身又是一颗树,并且称为根的子树(SubTree)。
??这个定义用了递归的概念,在树的知识中,这种定义方法非常常见。
?2.结点的度 叶结点 树的度
🍛1. 结点的度(Degree)
??结点拥有的子树数称为结点的度。
🍛2. 叶结点(Leaf)
??度为0的结点.
🍛3. 树的度
??树的度是树内部各结点的度的最大值。
?3.结点间的关系
??节点的子树的根称为节点的孩子(Child),相应的,该节点称为孩子的双亲。
??同一个双亲的孩子之间互称兄弟。
??结点的祖先是从根到该结点所经分支上的所有结点。
??以某结点为根的子树中的任一节点都称为该结点的子孙。
?4.树的其他概念
结点的层次
如果将树中结点的各子树看成从左至右是有次序的,不能互换的,则称该树为有序树,否则称为无序树。
森林是m课互不相交的树的集合。
?5.树的存储结构
🥘1. 双亲表示法
//双亲表示法
#define MAXSIZE 100//最多的节点个数
typedef int TDatatype;//方便后续修改
//单个结点
typedef struct {
TDatatype data;//数据域
int parent;//双亲域
int firstchild;//长子
int rightsub;//右兄弟域
}Node;
//具体要怎么设计节点中的内容可以根据基于该存储结构的运算是否合适是否方便来决定。
//整个树的空间
typedef struct {
int root;//根的位置
int n;//节点数
Node nodes[MAXSIZE];
}PTree;
🥘2. 孩子表示法
#define MAXSIZE 100//本树的最多的节点个数
//树的孩子表示法
//首先用一个链表表示树中一个结点的所有孩子节点
//这个链表的节点(非头结点)
typedef struct NODE{
int child;
struct NODE* next;
}*childptr;
//这个链表的头结点的内容是这个节点的数据和它的第一个孩子
typedef struct {
TDatatype data;
childptr firstchild;
}treeelement;
//把这个头结点再组成一个数组。
typedef struct {
treeelement nodes[MAXSIZE];
int root;
int n;//节点数
}CTree;
🥘3. 孩子兄弟表示法
/孩子兄弟表示法
//观察发现,对于一个二叉树来说,他的长子和右兄弟如果存在那么一定唯一 所以我们可以这样设计
typedef struct CBNode {
TDatatype data;
CBNode* firstchild;
CBNode* rightbro;
CBNode* parent;//加这个方便搜索自己的双亲
}CBTnode,*CBTree;
//这样的好处是我们把一个复杂的书变成了一棵二叉树 就可以充分的利用二叉树的性质来计算了
?6.二叉树的存储结构
🍲1.顺序存储
按照补全程对应完全二叉树的号来存,不存在的位置则存空。由于太浪费空间,所以一般只用来存完全二叉树。
🍲2.链式存储
存自己的左孩子,右孩子,如果需要快速查双亲信息则再加一个双亲域
//二叉树的链式存储
typedef struct BiTNode {
TDatatype data;
BiTNode* leftchild;
BiTNode* rightchild;
BiTNode* parent;
}BiTNode,*BiTree;
?7.二叉树的遍历
??二叉树的遍历是指从根节点出发,按照某种次序一次访问二叉树中的所有结点,使得每个节点被访问一次且仅被访问一次。
🥫1.前序遍历
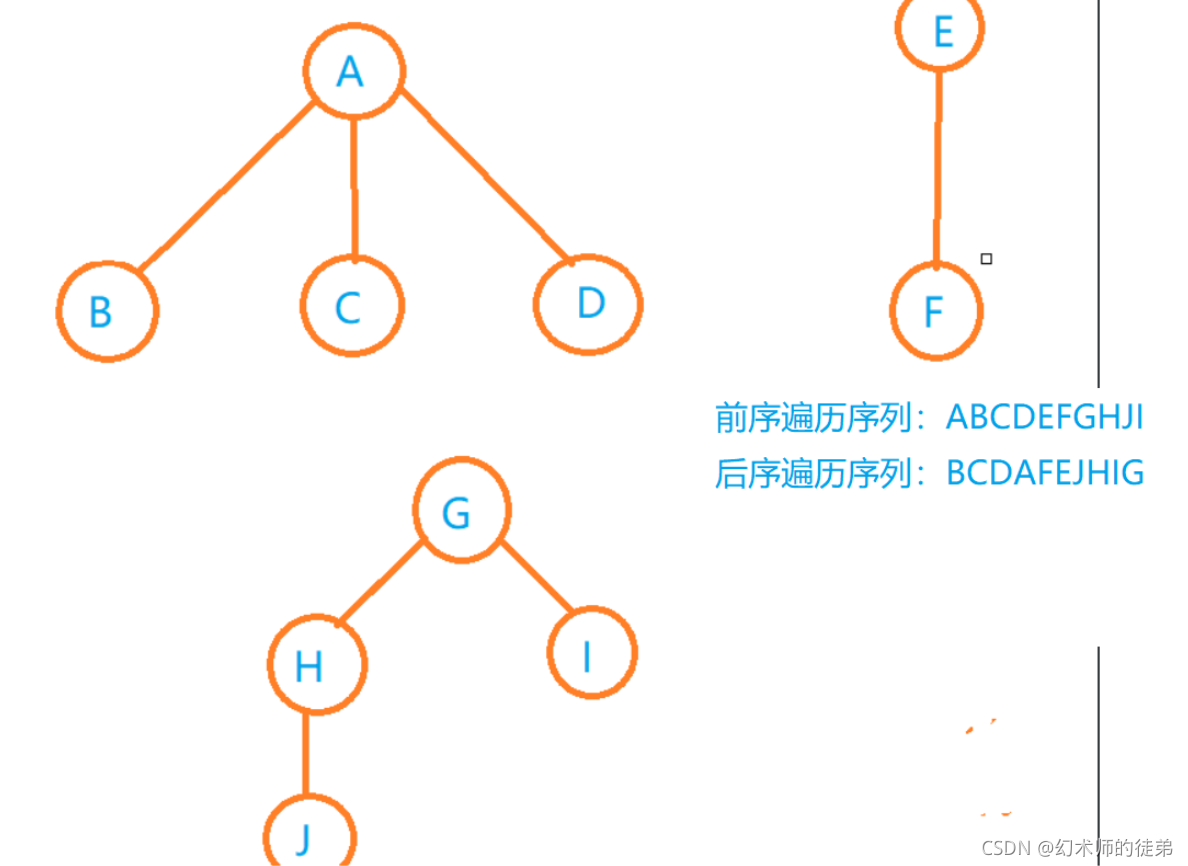
??规则是若二叉树为空,则空操作并返回;否则先访问根节点,然后前序遍历左子树,再前序遍历右子树。
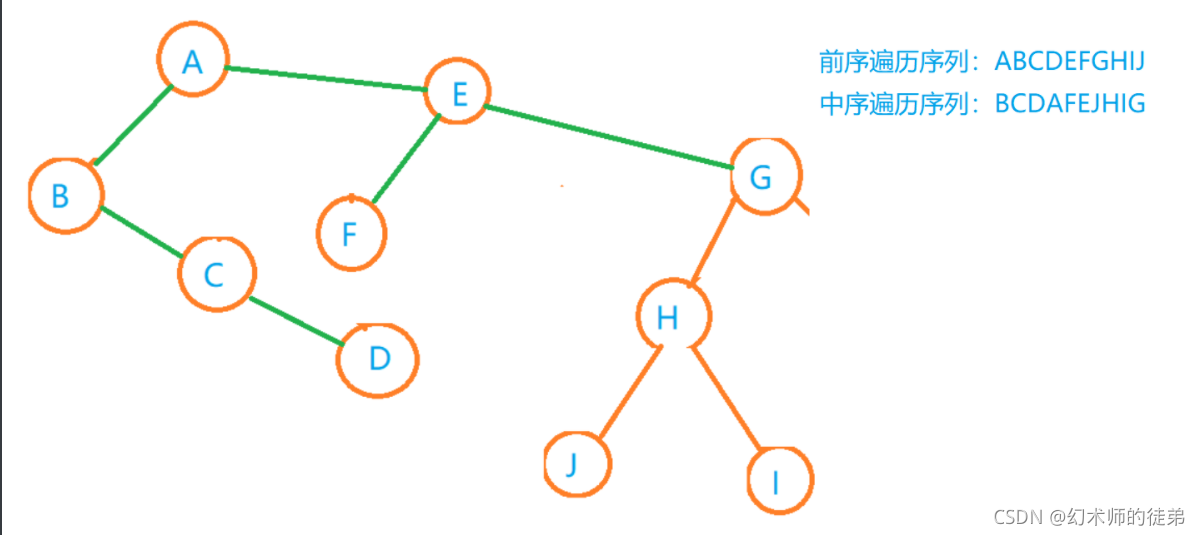
🥫2.中序遍历
??规则是若树为空,则空操作返回;否则从根节点开始,中序遍历根节点的左子树,然后访问根节点,然后中序遍历右子树。
🥫3.后序遍历
??规则是若树是空的,那么就空操作且返回,否则从左到右先叶子后节点的方式遍历左右子树,最后是访问根节点。
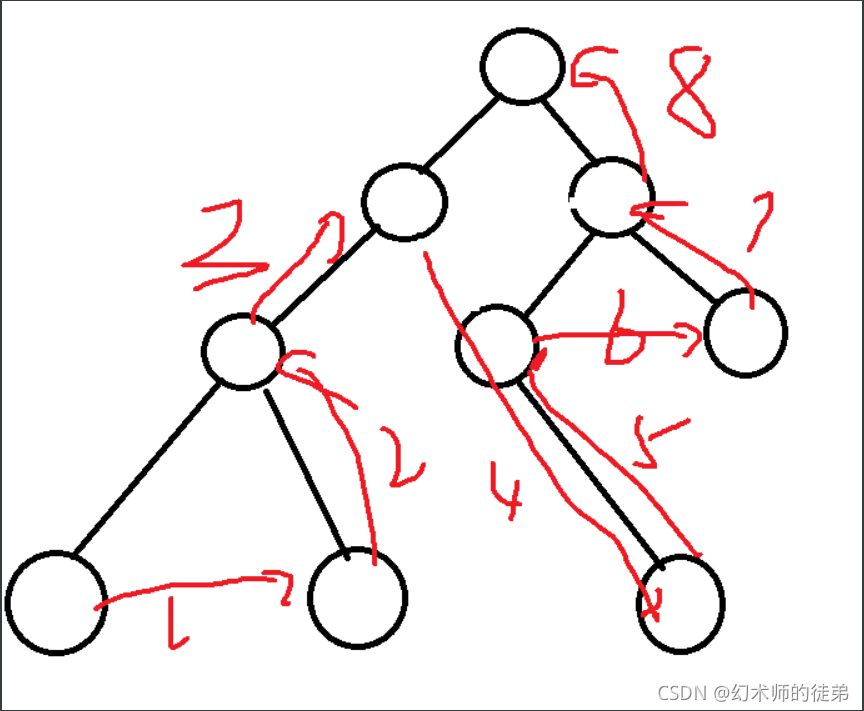
🥫4.层次遍历
??从上到下,从左到右依次遍历。
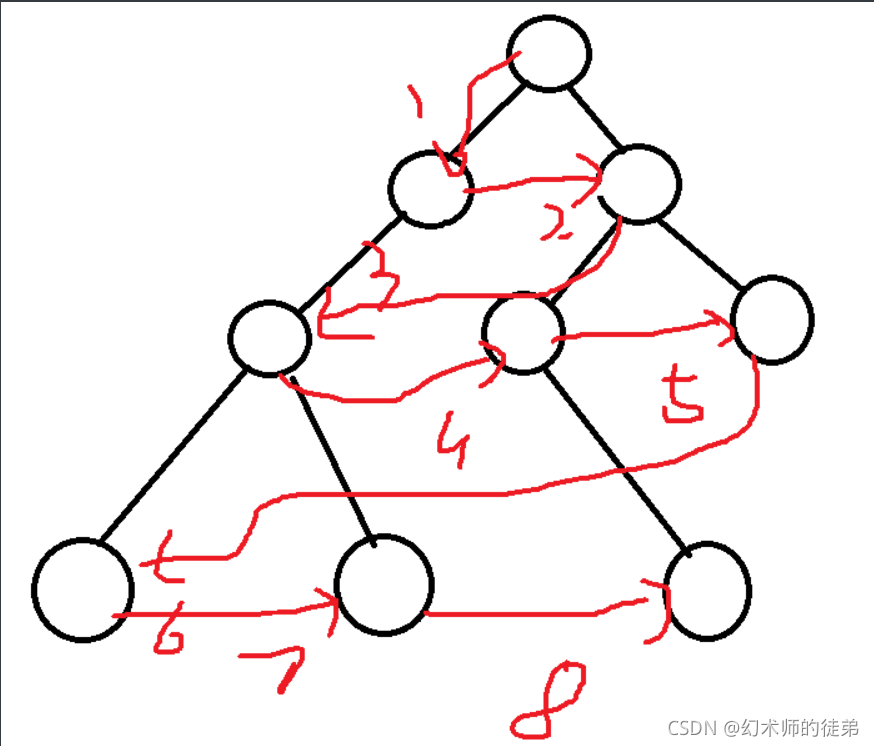
?8. 二叉树的遍历算法
🍜1.前序遍历算法
void PreOrderTraverse(BiTree T)
{
if (T == NULL)
{
return;
}
printf("%d ", T->data);
PreOrderTraverse(T->leftchild);
PreOrderTraverse(T->rightchild);
}
🍜2.中序遍历算法
void InOrderTraverse(BiTree T)
{
if (T == NULL)
{
return;
}
InOrderTraverse(T->leftchild);
printf("%d ", T->data);
InOrderTraverse(T->rightchild);
}
🍜3.后序遍历算法
void PostOrderTraverse(BiTree T)
{
if (T == NULL)
{
return;
}
PostOrderTraverse(T->leftchild);
PostOrderTraverse(T->rightchild);
printf("%c ", T->data);
}
??这个所谓的序,就是实际“访问”节点的顺序在访问结点对应左子树 访问结点对应的右子树的前面、中间、后面。
?9. 二叉树遍历结果的意义
- 已知前序遍历序列和中序遍历序列,可以唯一确定一颗二叉树。
- 已知中序遍历序列和后续遍历序列,可以唯一确定一颗二叉树。
??前序和后序在本质上都是将父节点与子结点进行分离,但并没有指明左子树和右子树的能力,(没有说明到哪里左子树遍历结束,到哪里右子树遍历结束)因此得到这两个序列只能明确父子关系,而不能确定一个二叉树。
??已知前序排列或者已知后续排列某种程度上都是会知道根是谁,前序会知道谁是自己的左孩子,后序会知道谁是自己的右孩子,但它们都没有严格指明左子树遍历到哪里结束,右子树遍历到哪里结束,而再加上中序排列会知道左子树在哪里遍历结束(因为会打印自己的节点),会知道右子树在哪里开始遍历(因为知道根),会知道右子树在哪里结束(因为中序打印完右子树会打印自己双亲节点,而这某种程度上是一种根,通过前序和后续都可以知道),因此我们知道了根在那和左右子树在那开始在哪结束,然后每个子树可以这样递归下去,因此就唯一确定了一颗子树。
??已知前序遍历序列和后序遍历序列,无法唯一确定一颗二叉树。
??如前序遍历结果ABC,后序遍历序列CBA
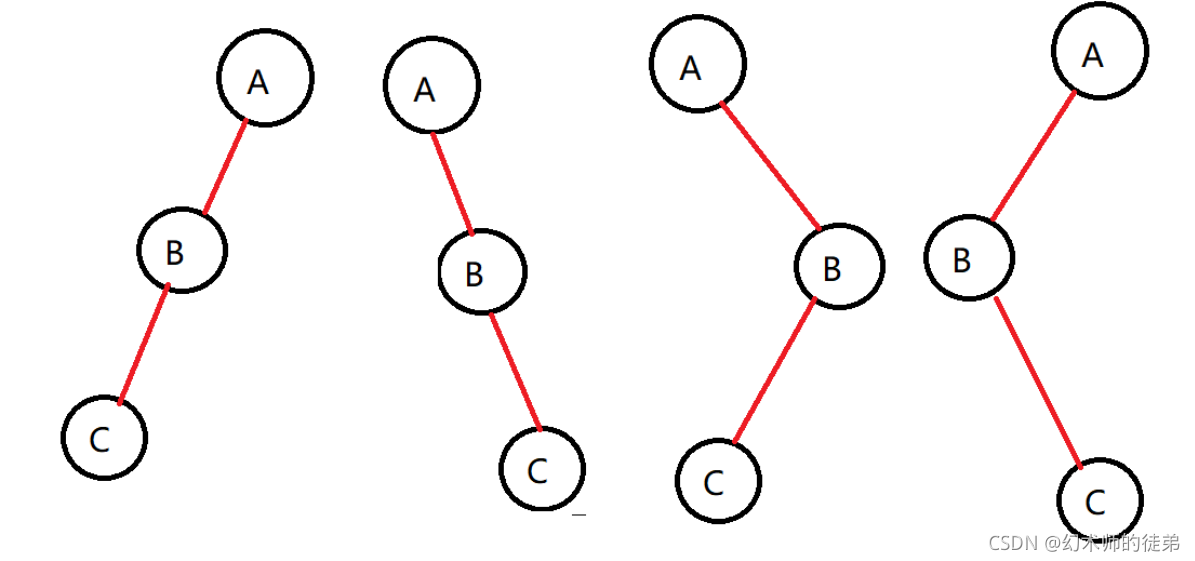
?10. 二叉树的建立
??我们利用了一个原理,拓展二叉树可以用先序或后序序列唯一确定一颗二叉树,而中序不可以
Proof:
??所谓拓展二叉树,就是保证除’#‘结点外,每个节点都有左孩子和右孩子,如果缺少左孩子或右孩子,就用’#'补上。
??对于先序排列,我根据先序排列会知道谁是根,谁是我的左孩子,加上拓展二叉树后,我会知道左子树在哪里结束(因为结尾肯定是##),也就知道了右子树在哪开始(即右孩子的位置),然后也会知道右子树的结束位置(##),以此递归,我就会唯一确定整颗子树。
??对于中序排列,其实我的拓展二叉树已经交待了区分左右子树的方法,但是你不能告诉我根,所以我们确定不了
??对于后序排列,我根据后序排列知道谁是根,谁是我的右孩子,加上了拓展二叉树后,我会知道右子树在哪里结束(结尾肯定是从右往左数经过两个##),也就知道了左子树在哪里开始(即左孩子的位置),也会知道左子树结束的位置(##),以此递归,我就会唯一确定整颗二叉树。
所以我们考虑用拓展二叉树的先序排列创建一棵二叉树。
int index = 0;//用一个全局变量来表示遍历到那个序列的哪个位置了
void CreateBiTree(BiTree* T,char* arr)
{
char ch = arr[index++];
if (ch == '#')
{
*T = NULL;
}
else
{
BiTree tmp = (BiTree)malloc(sizeof(BiTNode));
if (tmp == NULL)
{
printf("malloc fault\n");
exit(-1);
}
*T = tmp;
(*T)->data = ch;
CreateBiTree(&((*T)->leftchild),arr);
CreateBiTree(&((*T)->rightchild),arr);
}
}
?11. 二叉树的汇总
//BiTree.h
//二叉树的链式存储
#pragma once
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define MAXSIZE 1000
typedef char TDatatype;
typedef struct BiTNode {
TDatatype data;
struct BiTNode* leftchild;
struct BiTNode* rightchild;
struct BiTNode* parent;
}BiTNode,*BiTree;
//前序遍历算法
void PreOrderTraverse(BiTree T);
//中序遍历算法
void InOrderTraverse(BiTree T);
//后续遍历算法
void PostOrderTraverse(BiTree T);
//利用拓展二叉树(#法)的先序排列确定一棵二叉树
void CreateBiTree(BiTree* T,char* arr);
//int index = 0;//用来表示这个先序序列走到哪一位了
//BiTree.c
#include "BiTree.h"
void PreOrderTraverse(BiTree T)
{
if (T == NULL)
{
return;
}
printf("%c ", T->data);
PreOrderTraverse(T->leftchild);
PreOrderTraverse(T->rightchild);
}
void InOrderTraverse(BiTree T)
{
if (T == NULL)
{
return;
}
InOrderTraverse(T->leftchild);
printf("%c ", T->data);
InOrderTraverse(T->rightchild);
}
void PostOrderTraverse(BiTree T)
{
if (T == NULL)
{
return;
}
PostOrderTraverse(T->leftchild);
PostOrderTraverse(T->rightchild);
printf("%c ", T->data);
}
int index = 0;//用一个全局变量来表示遍历到那个序列的哪个位置了
void CreateBiTree(BiTree* T,char* arr)
{
char ch = arr[index++];
if (ch == '#')
{
*T = NULL;
}
else
{
BiTree tmp = (BiTree)malloc(sizeof(BiTNode));
if (tmp == NULL)
{
printf("malloc fault\n");
exit(-1);
}
*T = tmp;
(*T)->data = ch;
CreateBiTree(&((*T)->leftchild),arr);
CreateBiTree(&((*T)->rightchild),arr);
}
}
/
#include "BiTree.h"
void test1()
{
BiTree testree;
printf("请输入这棵二叉树的拓展二叉树(#法)的先序排列\n");
char arr[2 * MAXSIZE + 2] = { 0 };
scanf("%s", arr);
CreateBiTree(&testree,arr);
PreOrderTraverse(testree);
printf("\n");
InOrderTraverse(testree);
printf("\n");
PostOrderTraverse(testree);
}
int main()
{
test1();
return 0;
}
?12.线索二叉树
🌳1.提出背景
typedef char TDatatype;
typedef struct BiTNode {
TDatatype data;
struct BiTNode* leftchild;
struct BiTNode* rightchild;
struct BiTNode* parent;
}BiTNode,*BiTree;
??观察我们的二叉树的节点结构,其实有很多空间都被我们浪费了,因为有的节点没有左孩子,有的结点没有右孩子,叶结点没有左右孩子,我们是否可以利用一下空闲的空间呢,比如我们让空闲的左孩子指针指向创建当前二叉树所用遍历序列的前继,让空闲的右孩子指针指向创建当前二叉树的遍历序列的后继。
??但是,我们还是有一些问题,我们怎么确定这个右(左)孩子指针指的是自己的右(左)孩子还是后继(前继)呢?
??我们可以再创建两个布尔量,0表示此指针是正常指向自己的孩子的,1表示此指针是指向自己的后继或前继,为了方便,干碎用一个枚举变量,Link(链)表示此指针是指向自己孩子的链,Thread表示此指针是指向自己前继或后继的线。
🌳2.线索二叉树的存储结构
typedef enum {
Link,
Thread
}PointerTag;
typedef struct BiThrNode {
TDatatype data;
struct BiThNode* leftchild;
struct BiThNode* rightchild;
PointerTag LTag;
PointerTag RTag;
}BiThrNode,*BiThrTree;
🌳3.中序序列线索二叉树的建立
🎃3.1 建立二叉树
int index1 = 0;
void createBiThrTree(BiThrTree* T, char* arr)
{
char ch = arr[index1++];
if (ch == '#')
{
*T = NULL;
}
else
{
BiThrTree tmp = (BiThrTree)malloc(sizeof(BiThrNode));
if (tmp == NULL)
{
printf("malloc fault\n");
exit(-1);
}
*T = tmp;
(*T)->data = ch;
(*T)->LTag = Link;
(*T)->RTag = Link;
createBiThrTree(&((*T)->leftchild), arr);
createBiThrTree(&((*T)->rightchild), arr);
}
}
🎃3.2 二叉树线索化
extern BiThrTree pre;
//把二叉树按中序遍历序列线索化
void InThreading(BiThrTree p)
{
if (p)
{
InThreading(p->leftchild);
if (!p->leftchild)
{
p->LTag = Thread;
p->leftchild = pre;
}
if (pre!=NULL)
{
if (!pre->rightchild)
{
pre->RTag = Thread;
pre->rightchild = p;
}
}
pre = p;
InThreading(p->rightchild);
}
}
🎃3.3 插入头结点
//为二叉树插入头结点
void addhead_IN(BiThrTree* T)
{
BiThrTree head = (BiThrTree)malloc(sizeof(BiThrNode));
head->LTag = Link;
head->RTag = Thread;
head->leftchild = (*T);
BiThrTree p = *T;
//先把中序遍历的第一个结点的前继指针指向头结点
while (p->LTag == Link)
{
p = p->leftchild;
}
p->leftchild = head;
//下面我们让p指向中序遍历序列的最后一个结点
while (p->rightchild != NULL)
{
while (p->LTag == Link)
p = p->leftchild;
while (p->RTag == Thread && p->rightchild != NULL)
{
p = p->rightchild;
}
p = p->rightchild;//进入它的右子树
}
p->rightchild = head;
p->RTag = Thread;
head->rightchild = p;
*T = head;
}
🎃3.4 遍历线索二叉树
//中序遍历线索二叉树
void InOrderTraverse_Thr(BiThrTree T)
{
BiThrTree p;
p = T->leftchild;
if (p == NULL)
{
printf("线索二叉树为空\n");
return;
}
while (p != T)
{
while (p->LTag == Link)
p = p->leftchild;
printf("%c ", p->data);
while (p->RTag == Thread && p != T)
{
p = p->rightchild;
if (p == T)
{
break;
}
printf("%c ", p->data);
}
//到这里说明左子树遍历完了 该进入右子树了
if (p != T)
{
p = p->rightchild;
}
}
}
🌳4.前序序列线索二叉树的建立
extern BiThrTree pre1;
//按照前序遍历序列线索化二叉树
void PreThreading(BiThrTree p)
{
if (p != NULL)
{
if (p->leftchild == NULL)
{
p->LTag = Thread;
p->leftchild = pre1;
}
if (pre1 != NULL)
{
if (pre1->rightchild == NULL)
{
pre1->RTag = Thread;
pre1->rightchild = p;
}
}
pre1 = p;
if (p->LTag == Link)
{
PreThreading(p->leftchild);
}
if (p->RTag == Link)
{
PreThreading(p->rightchild);
}
}
}
//插头结点
void addhead_Pre(BiThrTree* T)
{
BiThrTree head = (BiThrTree)malloc(sizeof(BiThrNode));
if (head == NULL)
{
printf("malloc fault\n");
return;
}
head->LTag = Link;
head->leftchild = *T;
head->RTag = Thread;
BiThrTree p = *T;
while (p->rightchild != NULL)
{
while (p->LTag==Link)
p = p->leftchild;
while (p->RTag == Thread && p->rightchild!=NULL)
p = p->rightchild;
}
p->RTag = Thread;
head->rightchild = p;
p->rightchild = head;
*T = head;
}
//前序遍历线索二叉树
void PreOrderTraverse_Thr(BiThrTree T)
{
BiThrTree p = T->leftchild;
printf("%c ", p->data);
while (p != T)
{
//printf("%c ", p->data);
while (p->LTag == Link)
{
p = p->leftchild;
printf("%c ", p->data);
}
while (p->RTag == Thread && p!=T)
{
p = p->rightchild;
if (p != T)
{
printf("%c ", p->data);
}
}
}
}
🌳5.后序序列线索二叉树的建立(遍历函数待研究)
extern BiThrTree pre2;
void PostThreading(BiThrTree p)
{
if (p)
{
PostThreading(p->leftchild);
PostThreading(p->rightchild);
if (p->leftchild == NULL)
{
p->LTag = Thread;
p->leftchild = pre2;
}
if (pre2 != NULL)
{
if (pre2->rightchild == NULL)
{
pre2->RTag = Thread;
pre2->rightchild = p;
}
}
pre2 = p;
}
}
void addhead_Post(BiThrTree* T)
{
BiThrTree head = (BiThrTree)malloc(sizeof(BiThrNode));
if (head == NULL)
{
printf("malloc fault\n");
return;
}
head->LTag = Link;
head->leftchild = *T;
head->RTag = Thread;
BiThrTree p = *T;
while (p->LTag == Link)
p = p->leftchild;
p->LTag = Thread;
p->leftchild = head;
head->rightchild = *T;
if ((*T)->rightchild == NULL)
{
(*T)->rightchild = head;
}
*T = head;
}
void PostOrderTraverse_Thr(BiThrTree T)
//开发失败 寄了
{
BiThrTree p;
p = T->leftchild;
if (p == NULL)
{
printf("线索二叉树为空\n");
return;
}
while (p != T)
{
while (p->LTag == Link)
p = p->leftchild;
printf("%c ", p->data);
while (p->RTag == Thread && p != T)
{
p = p->rightchild;
if (p == T)
{
break;
}
printf("%c ", p->data);
}
//到这里说明左子树遍历完了 该进入右子树了
if (p != T)
{
p = p->rightchild;
}
}
}
🌳6. 线索二叉树的汇总
//BiThrTree.h
#pragma once
//线索二叉树
typedef enum {
Link,
Thread
}PointerTag;
typedef struct BiThrNode {
TDatatype data;
struct BiThNode* leftchild;
struct BiThNode* rightchild;
PointerTag LTag;
PointerTag RTag;
}BiThrNode,*BiThrTree;
void createBiThrTree(BiThrTree* T,char* arr);
void print(BiThrTree T);
//按照中序遍历序列给把二叉树线索化
BiThrTree pre;
void InThreading(BiThrTree p);
void addhead_IN(BiThrTree* T);
void InOrderTraverse_Thr(BiThrTree T);
//按照前序遍历序列把二叉树线索化
BiThrTree pre1;
void PreThreading(BiThrTree p);
void addhead_Pre(BiThrTree* T);
//中序遍历线索二叉树
void PreOrderTraverse_Thr(BiThrTree T);
//按照后序遍历序列把二叉树线索化
BiThrTree pre2;
//按照拓展二叉树的后续遍历序列创建二叉树
void createBiThrTree_Post(BiThrTree* T, char* str);//待研究
void PostThreading(BiThrTree p);
void addhead_Post(BiThrTree* T);
void PostOrderTraverse_Thr(BiThrTree T);//待研究
//BiThrTree.c
#include "BiThrTree.h"
int index1 = 0;
void createBiThrTree(BiThrTree* T, char* arr)
{
char ch = arr[index1++];
if (ch == '#')
{
*T = NULL;
}
else
{
BiThrTree tmp = (BiThrTree)malloc(sizeof(BiThrNode));
if (tmp == NULL)
{
printf("malloc fault\n");
exit(-1);
}
*T = tmp;
(*T)->data = ch;
(*T)->LTag = Link;
(*T)->RTag = Link;
createBiThrTree(&((*T)->leftchild), arr);
createBiThrTree(&((*T)->rightchild), arr);
}
}
void print(BiThrTree T)
{
if (T == NULL)
{
return;
}
printf("%c ", T->data);
print(T->leftchild);
print(T->rightchild);
}
extern BiThrTree pre;
//把二叉树按中序遍历序列线索化
void InThreading(BiThrTree p)
{
if (p)
{
InThreading(p->leftchild);
if (!p->leftchild)
{
p->LTag = Thread;
p->leftchild = pre;
}
if (pre!=NULL)
{
if (!pre->rightchild)
{
pre->RTag = Thread;
pre->rightchild = p;
}
}
pre = p;
InThreading(p->rightchild);
}
}
//为二叉树插入头结点
void addhead_IN(BiThrTree* T)
{
BiThrTree head = (BiThrTree)malloc(sizeof(BiThrNode));
head->LTag = Link;
head->RTag = Thread;
head->leftchild = (*T);
BiThrTree p = *T;
//先把中序遍历的第一个结点的前继指针指向头结点
while (p->LTag == Link)
{
p = p->leftchild;
}
p->leftchild = head;
//下面我们让p指向中序遍历序列的最后一个结点
while (p->rightchild != NULL)
{
while (p->LTag == Link)
p = p->leftchild;
while (p->RTag == Thread && p->rightchild != NULL)
{
p = p->rightchild;
}
p = p->rightchild;//进入它的右子树
}
p->rightchild = head;
p->RTag = Thread;
head->rightchild = p;
*T = head;
}
//中序遍历线索二叉树
void InOrderTraverse_Thr(BiThrTree T)
{
BiThrTree p;
p = T->leftchild;
if (p == NULL)
{
printf("线索二叉树为空\n");
return;
}
while (p != T)
{
while (p->LTag == Link)
p = p->leftchild;
printf("%c ", p->data);
while (p->RTag == Thread && p != T)
{
p = p->rightchild;
if (p == T)
{
break;
}
printf("%c ", p->data);
}
//到这里说明左子树遍历完了 该进入右子树了
if (p != T)
{
p = p->rightchild;
}
}
}
extern BiThrTree pre1;
//按照前序遍历序列线索化二叉树
void PreThreading(BiThrTree p)
{
if (p != NULL)
{
if (p->leftchild == NULL)
{
p->LTag = Thread;
p->leftchild = pre1;
}
if (pre1 != NULL)
{
if (pre1->rightchild == NULL)
{
pre1->RTag = Thread;
pre1->rightchild = p;
}
}
pre1 = p;
if (p->LTag == Link)
{
PreThreading(p->leftchild);
}
if (p->RTag == Link)
{
PreThreading(p->rightchild);
}
}
}
//插头结点
void addhead_Pre(BiThrTree* T)
{
BiThrTree head = (BiThrTree)malloc(sizeof(BiThrNode));
if (head == NULL)
{
printf("malloc fault\n");
return;
}
head->LTag = Link;
head->leftchild = *T;
head->RTag = Thread;
BiThrTree p = *T;
while (p->rightchild != NULL)
{
while (p->LTag==Link)
p = p->leftchild;
while (p->RTag == Thread && p->rightchild!=NULL)
p = p->rightchild;
}
p->RTag = Thread;
head->rightchild = p;
p->rightchild = head;
*T = head;
}
//前序遍历线索二叉树
void PreOrderTraverse_Thr(BiThrTree T)
{
BiThrTree p = T->leftchild;
printf("%c ", p->data);
while (p != T)
{
//printf("%c ", p->data);
while (p->LTag == Link)
{
p = p->leftchild;
printf("%c ", p->data);
}
while (p->RTag == Thread && p!=T)
{
p = p->rightchild;
if (p != T)
{
printf("%c ", p->data);
}
}
}
}
//int index2;
//void createBiThrTree_Post(BiThrTree* T, char* str)
//{
// char ch = str[index2++];
// if (ch == '#')
// {
// *T = NULL;
// }
// else
// {
// createBiThrTree_Post(&((*T)->leftchild), str);
// createBiThrTree_Post(&((*T)->rightchild), str);
// BiThrTree tmp = (BiThrTree)malloc(sizeof(BiThrNode));
// if (tmp == NULL)
// {
// printf("malloc fault\n");
// return;
// }
// tmp->data = ch;
// tmp->LTag = Link;
// tmp->RTag = Link;
// *T = tmp;
// }
//
//}
extern BiThrTree pre2;
void PostThreading(BiThrTree p)
{
if (p)
{
PostThreading(p->leftchild);
PostThreading(p->rightchild);
if (p->leftchild == NULL)
{
p->LTag = Thread;
p->leftchild = pre2;
}
if (pre2 != NULL)
{
if (pre2->rightchild == NULL)
{
pre2->RTag = Thread;
pre2->rightchild = p;
}
}
pre2 = p;
}
}
void addhead_Post(BiThrTree* T)
{
BiThrTree head = (BiThrTree)malloc(sizeof(BiThrNode));
if (head == NULL)
{
printf("malloc fault\n");
return;
}
head->LTag = Link;
head->leftchild = *T;
head->RTag = Thread;
BiThrTree p = *T;
while (p->LTag == Link)
p = p->leftchild;
p->LTag = Thread;
p->leftchild = head;
head->rightchild = *T;
if ((*T)->rightchild == NULL)
{
(*T)->rightchild = head;
}
*T = head;
}
//void PostOrderTraverse_Thr(BiThrTree T)
开发失败 寄了
//{
// BiThrTree p;
// p = T->leftchild;
// if (p == NULL)
// {
// printf("线索二叉树为空\n");
// return;
// }
// while (p != T)
// {
// while (p->LTag == Link)
// p = p->leftchild;
// printf("%c ", p->data);
// while (p->RTag == Thread && p != T)
// {
// p = p->rightchild;
// if (p == T)
// {
// break;
// }
// printf("%c ", p->data);
// }
// //到这里说明左子树遍历完了 该进入右子树了
// if (p != T)
// {
// p = p->rightchild;
// }
// }
//}
//test.c
#include "BiThrTree.h"
void test2()
{
BiThrTree testtree;
printf("请输入这棵二叉树的拓展二叉树(#法)的前序排列\n");
char arr[2 * MAXSIZE + 2] = { 0 };
scanf("%s", arr);
createBiThrTree(&testtree, arr);
print(testtree);
InThreading(testtree);
addhead_IN(&testtree);
printf("\n");
InOrderTraverse_Thr(testtree);
}
void test3()
{
BiThrTree testtree;
printf("请输入这棵二叉树的拓展二叉树(#法)的前序排列\n");
char arr[2 * MAXSIZE + 2] = { 0 };
scanf("%s", arr);
createBiThrTree(&testtree, arr);
print(testtree);
PreThreading(testtree);
addhead_Pre(&testtree);
printf("\n");
PreOrderTraverse_Thr(testtree);
}
void test4()
{
BiThrTree testtree;
printf("请输入这棵二叉树的拓展二叉树(#法)的前序排列\n");
char arr[2 * MAXSIZE + 2] = { 0 };
scanf("%s", arr);
createBiThrTree(&testtree, arr);
print(testtree);
PostThreading(testtree);
addhead_Post(&testtree);
}
int main()
{
test2();
test3();
test4();
return 0;
}
?13.树、森林与二叉树的转化
??我们费了那么大力气研究二叉树不仅仅是因为二叉树是一种很基础的树,更是因为树和森林都可以在某种程度上转化为二叉树,并且树、森林的前序遍历、后序遍历结果与我们转化出来的二叉树的前序遍历、中序遍历是一样的,下面我们来介绍这块的内容。
🌴1.树转化为二叉树
步骤:
- 加线:在所有兄弟节点之间加一条连线。
- 去线:对于树的每个节点,只保留它和第一个孩子结点的连线,删除它与其他孩子结点之间的连线。
- 层次调整:以树的根节点为轴心,将整棵树顺时针旋转一定的角度,使之结构层次分明。注意第一个孩子是二叉树结点的左孩子,兄弟转过来的孩子是结点的右孩子。
如图:
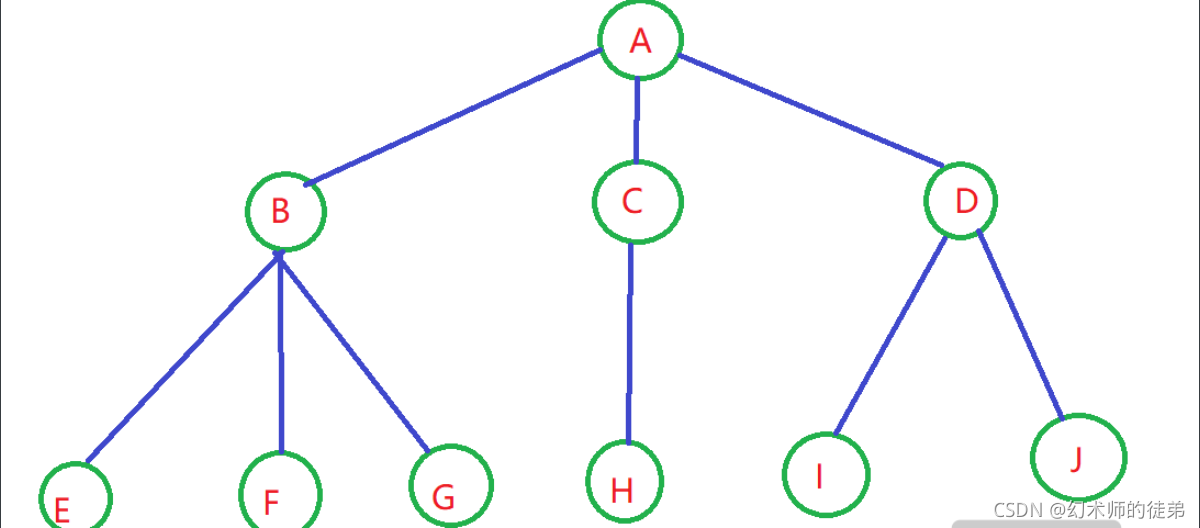
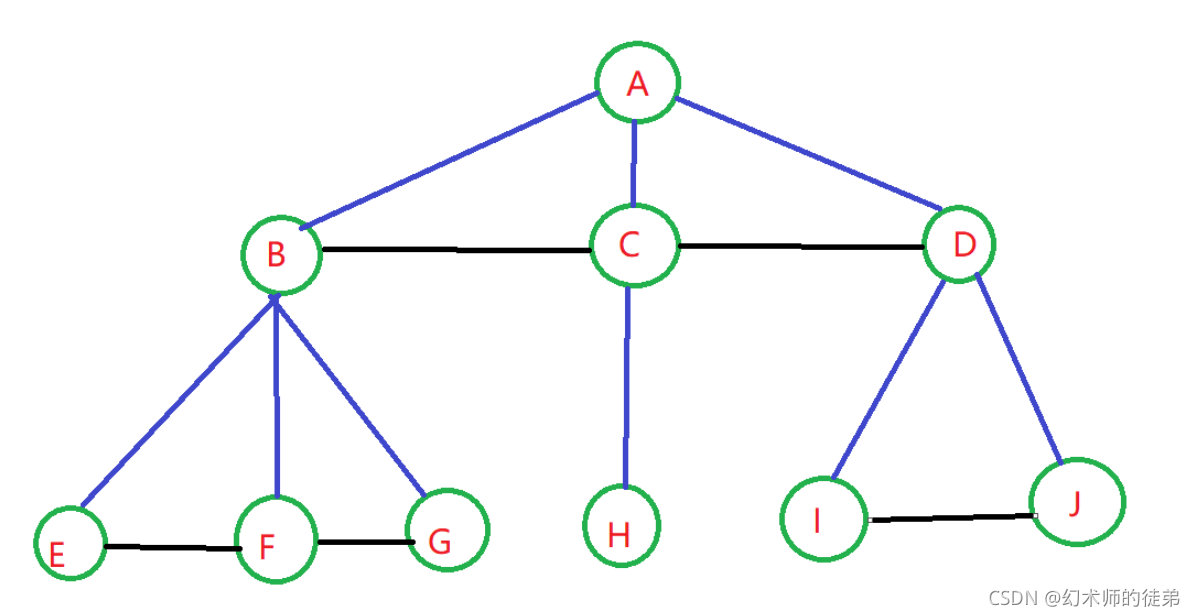
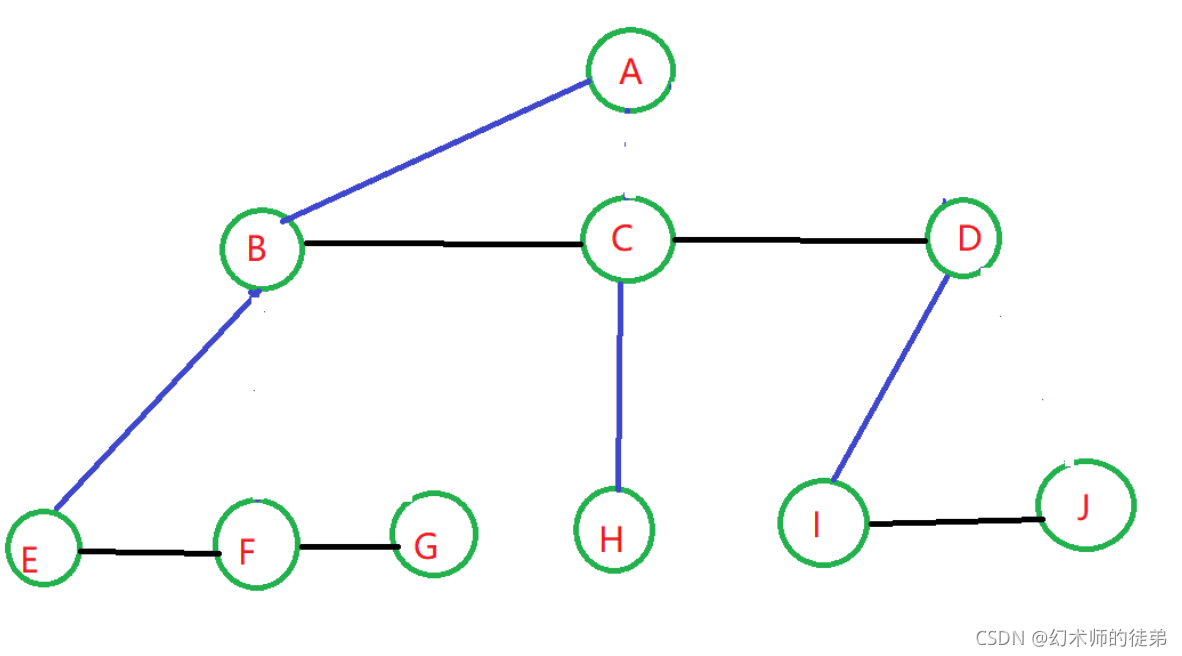
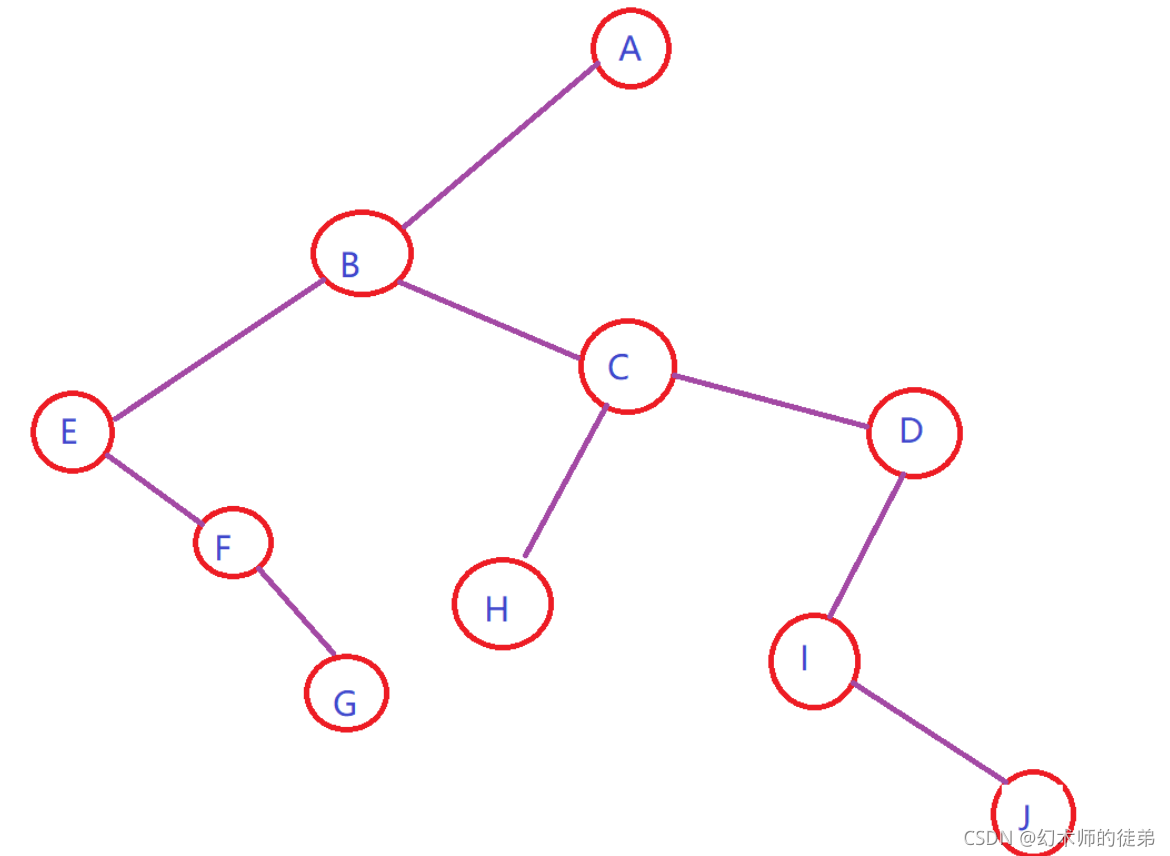
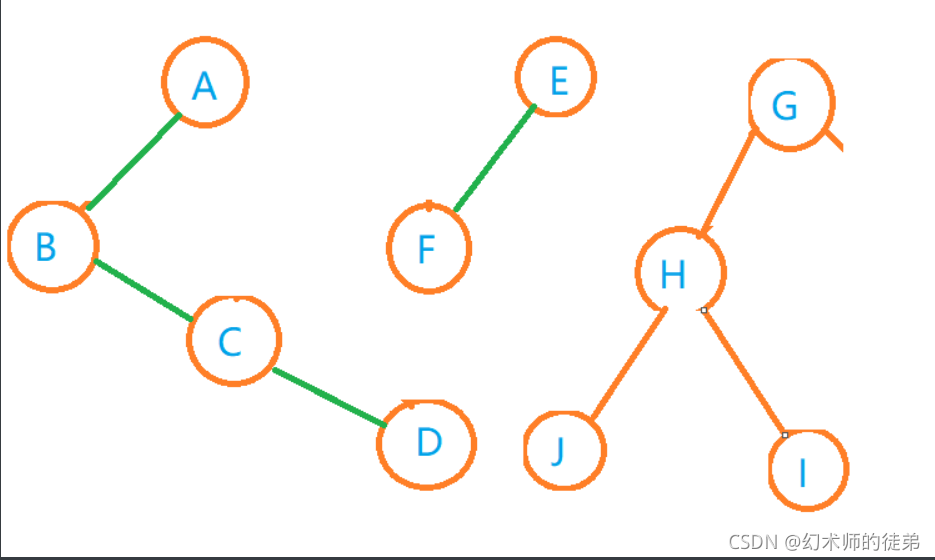
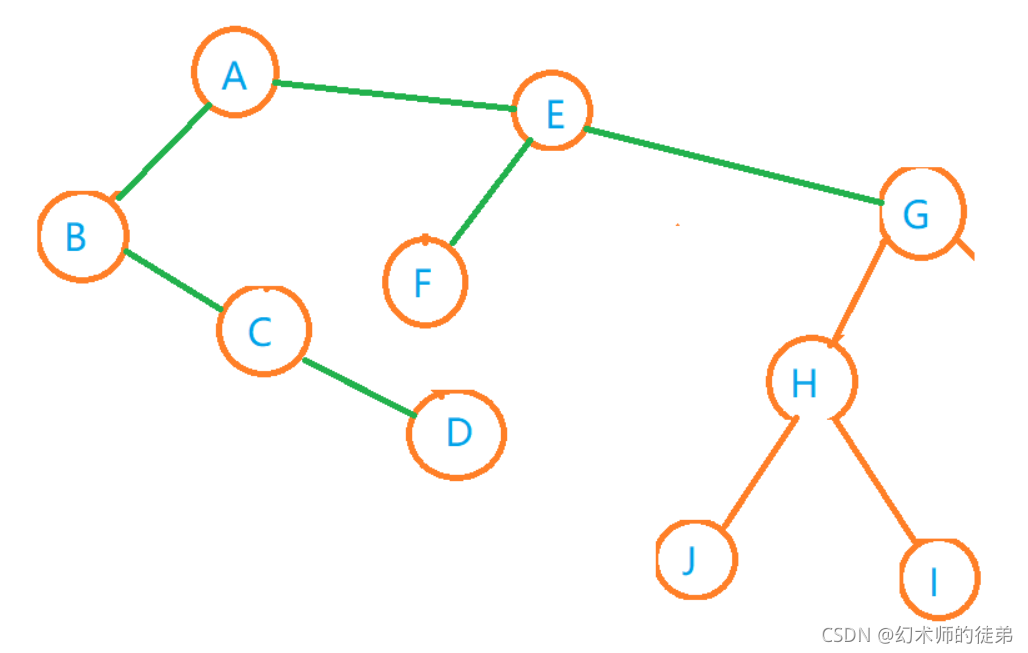
🌴2.森林转化为二叉树
- 把每个树转化为二叉树
- 第一棵树不动,从第二棵二叉树开始,依次把后一刻二叉树的根节点作为前一棵二叉树根节点的右孩子,用线连起来。
观察到这种转化转化出来的二叉树的根节点只有左孩子。
如图:
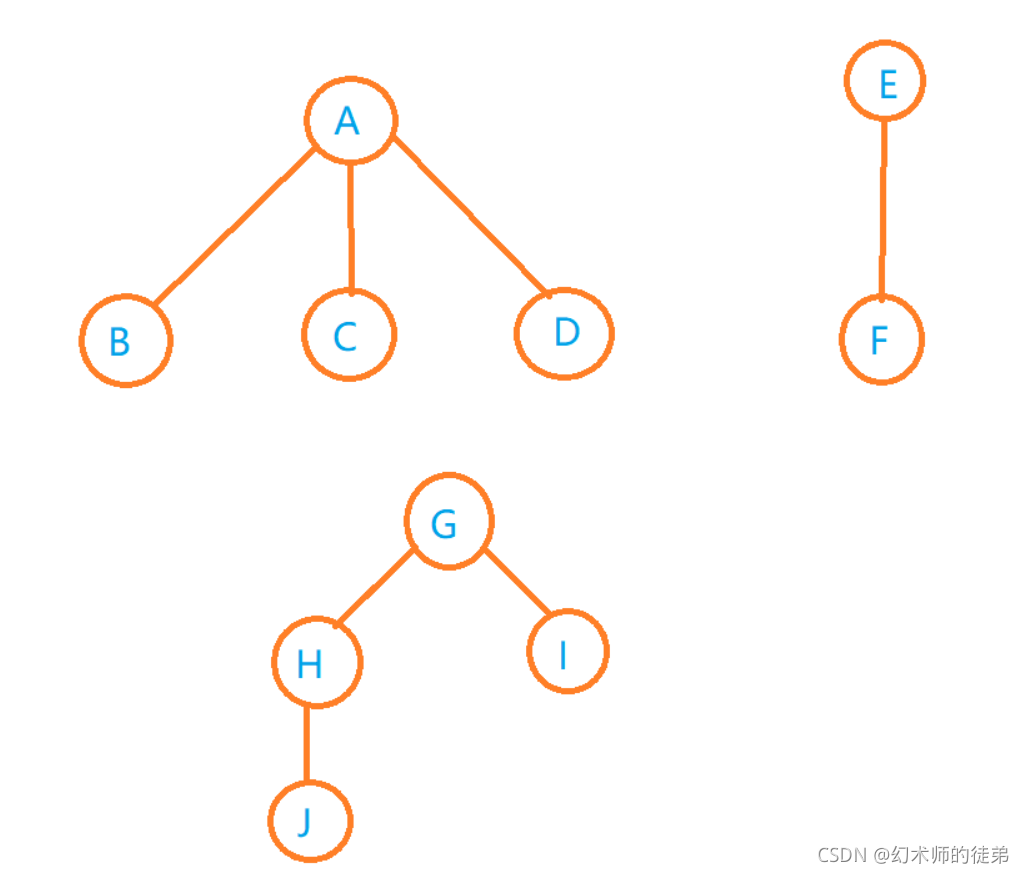
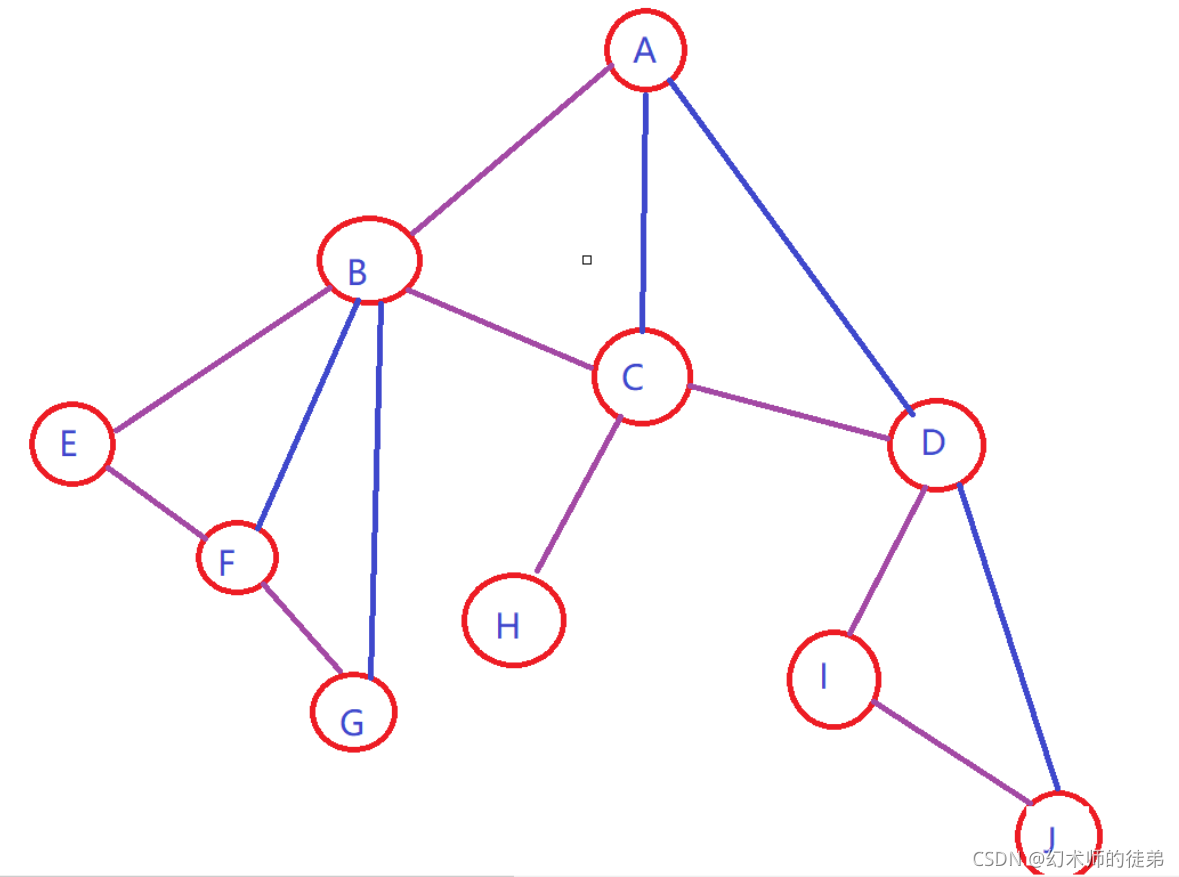
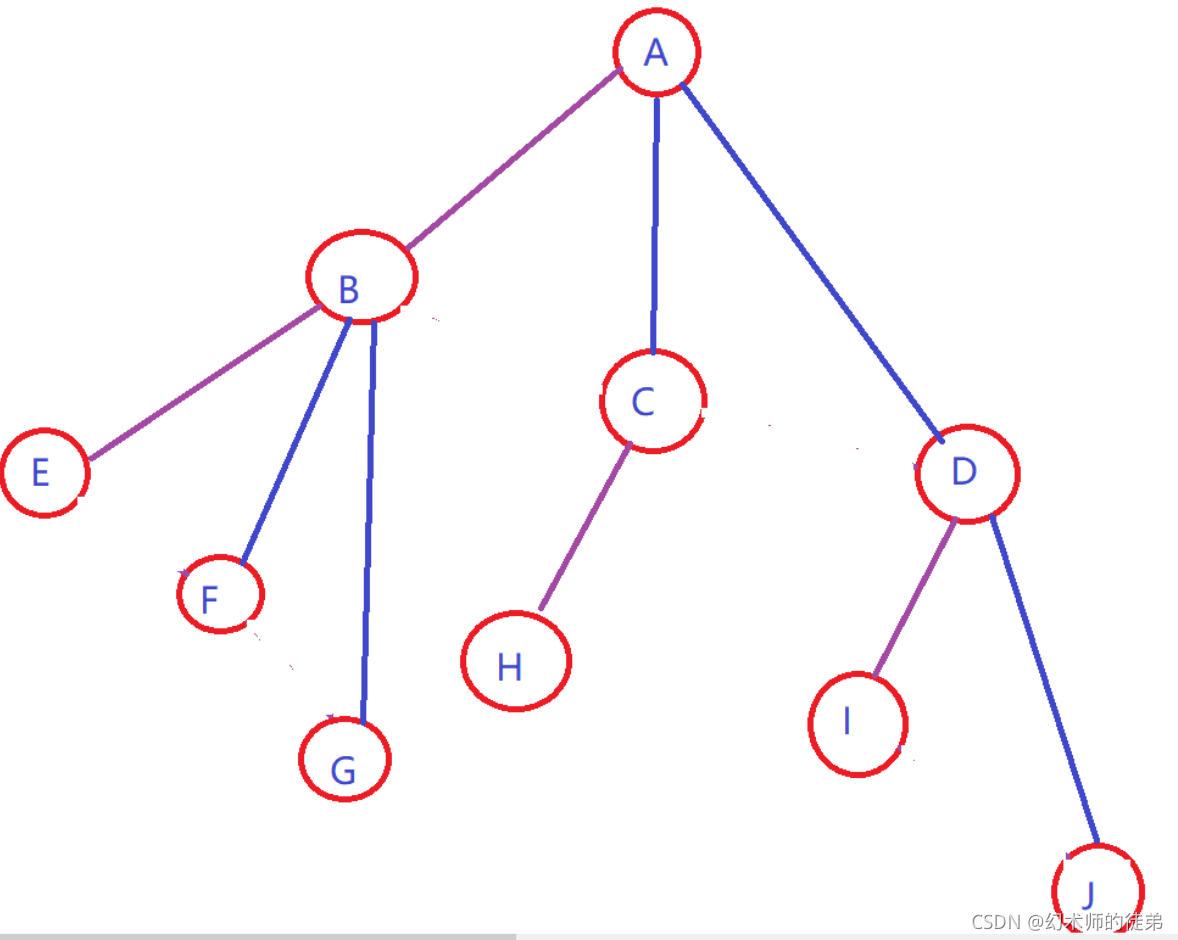
🌴3.二叉树转化为树
- 加线:若某结点的左孩子存在,在把这个左孩子的右孩子,左孩子的右孩子的右孩子。。。。左孩子的n层右孩子都作为此节点的孩子,并且连线连起来。
- 去线:删除原二叉树中所有结点与其右孩子的连线。
- 次序调整。
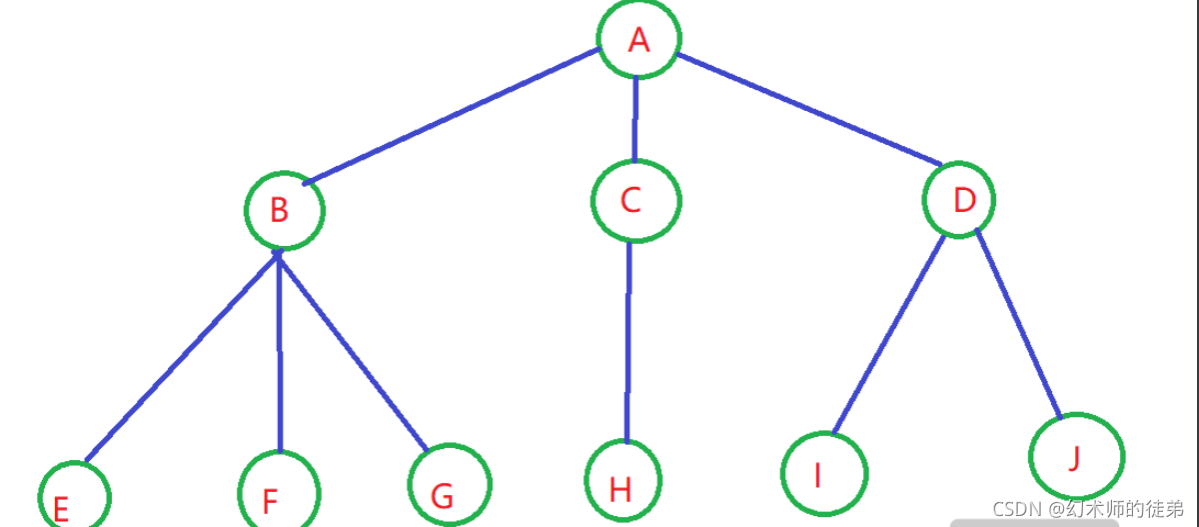
🌴4.二叉树转化为森林
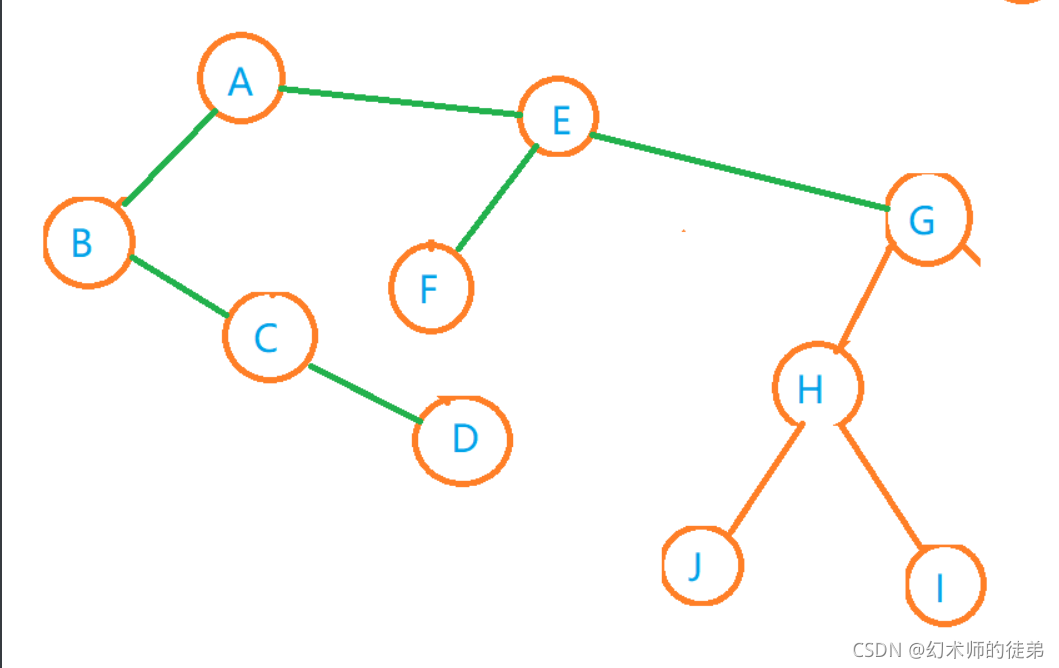
??首先要判断一棵二叉树是否能转化为一棵森林,很简单,只要看这棵二叉树的根节点有没有右孩子,如果有,那就是森林,如果没有,就是一棵树。
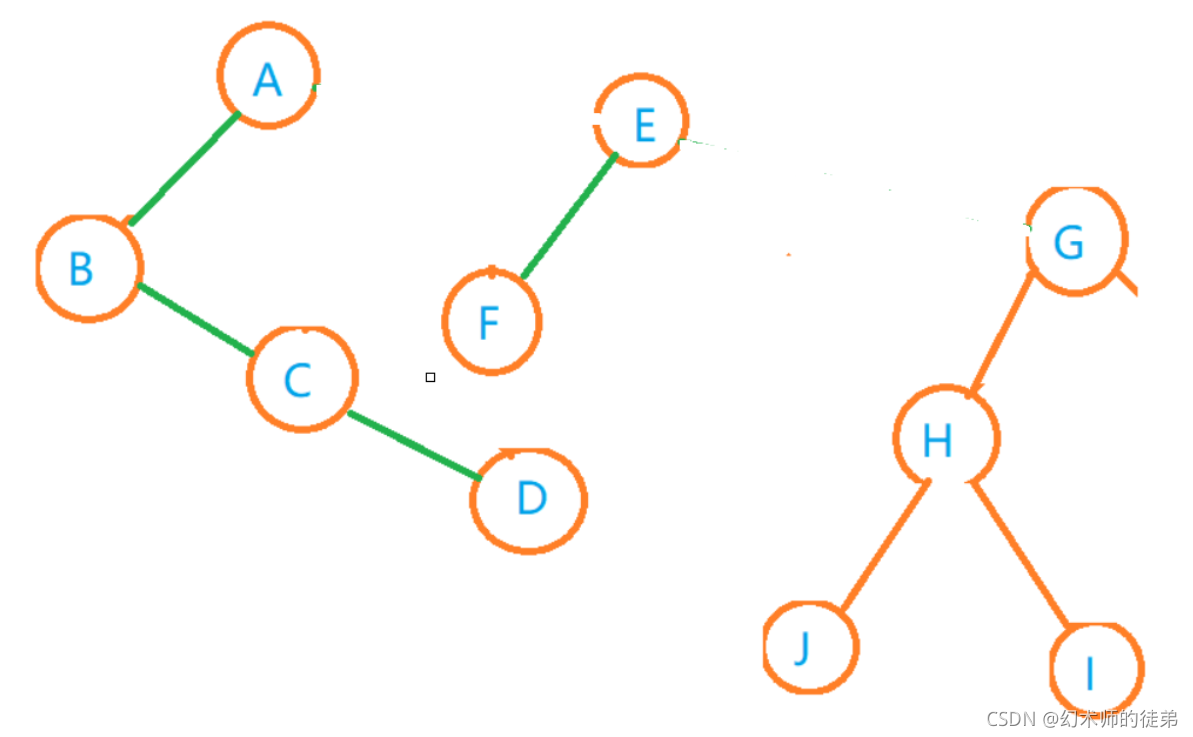
- 从根结点开始,如果右孩子存在,就把与右孩子结点的连线删除。
- 看去除后的二叉树,重复第一步,直到没有右孩子为止。
- 把每棵二叉树转化回普通的树。
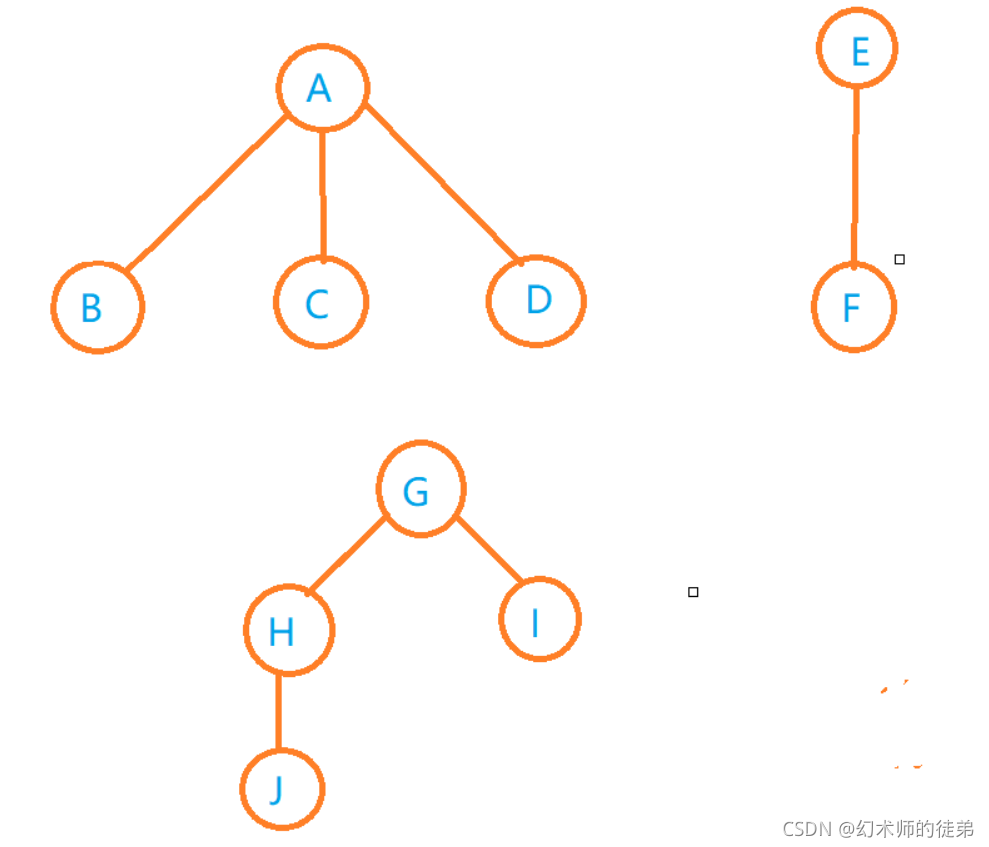
🌴5.树与森林的遍历
🔥5.1 树的遍历
🐱5.1.1 先根遍历
??先访问树的根结点,然后依次先根遍历根的每棵子树。
🐱5.1.2 后根遍历
??先依次后根遍历每棵子树,然后再访问根结点。
🔥5.2 森林的遍历
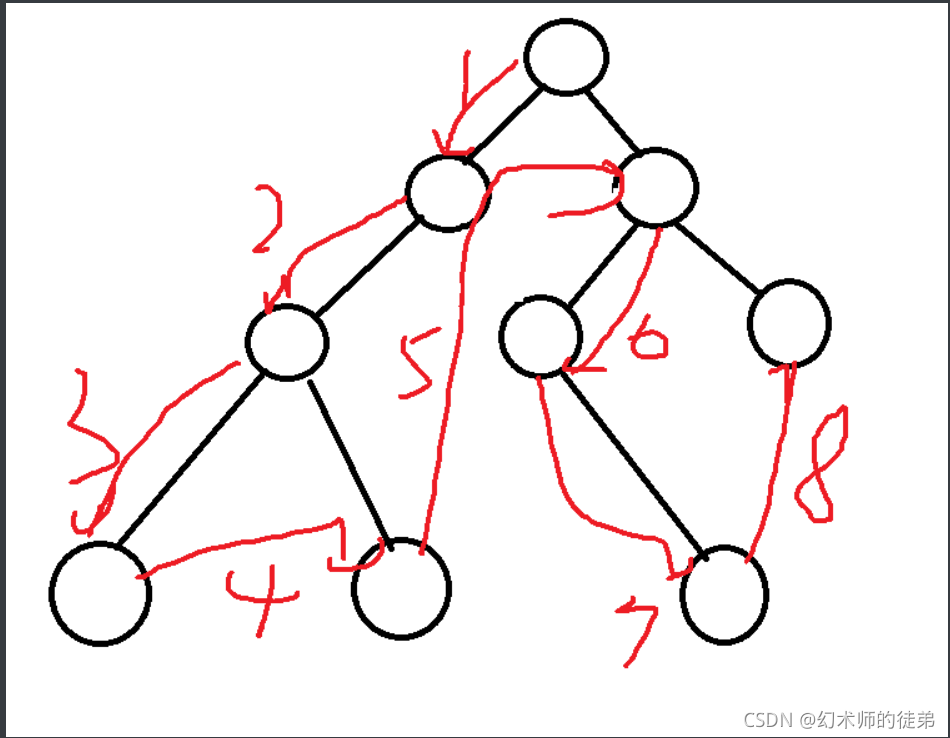
🐬5.2.1 前序遍历
??先访问森林中第一棵树的根结点,然后再依次先根遍历根的每棵子树,然后再依次遍历森林中的其他的树。
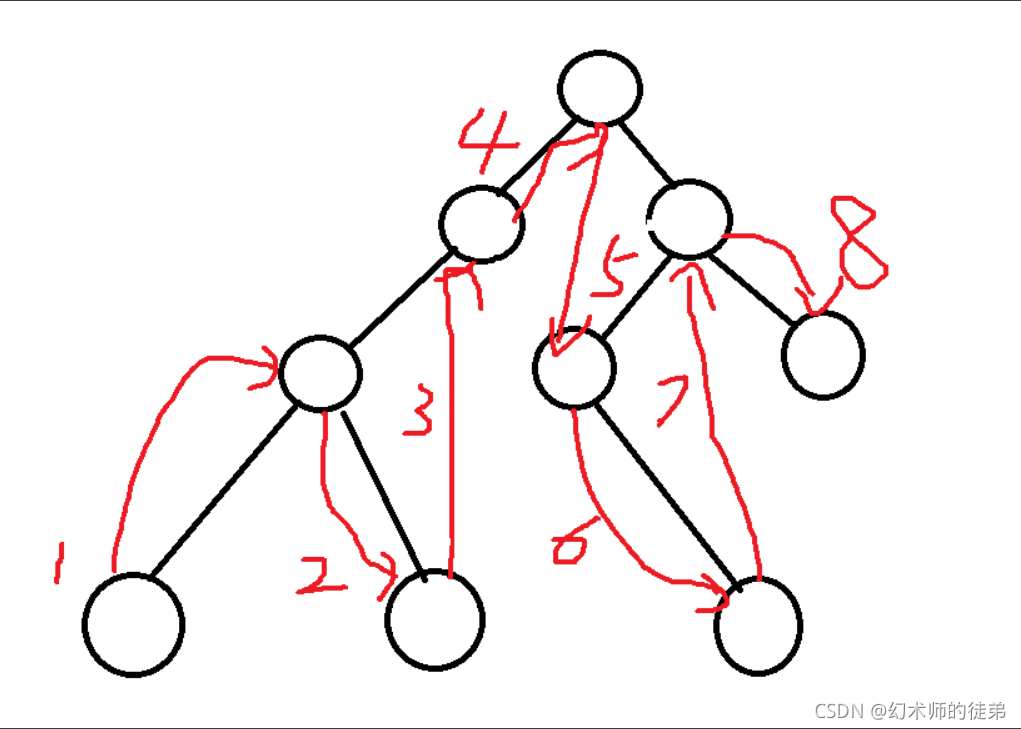
🐬5.2.2 后序遍历
??依次后根遍历森林中的每棵子树。
我们用个例子来说明树的先根遍历等价于转化出来的二叉树的前序遍历、树的后根遍历等价于转化出来的二叉树的中序遍历。
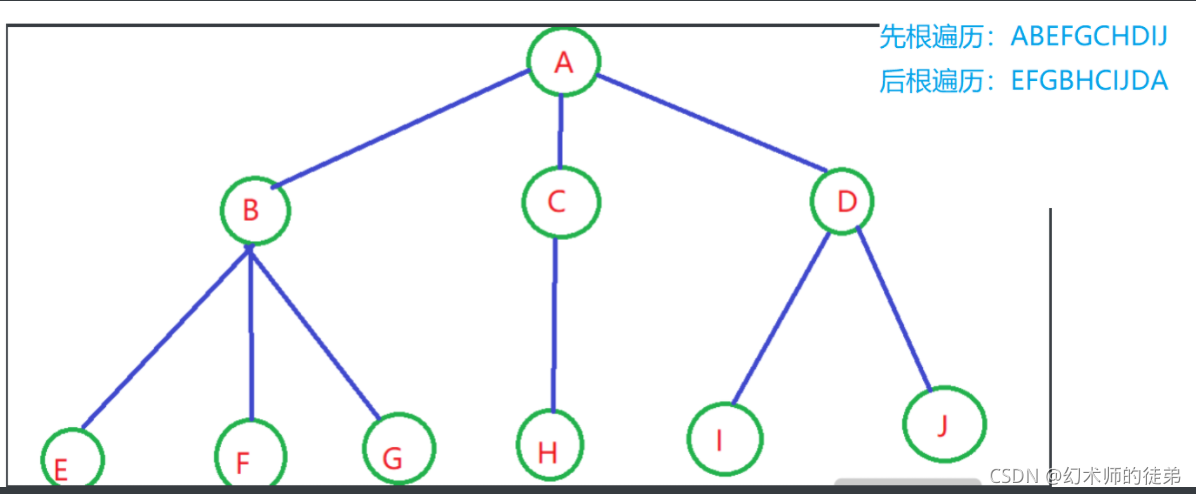
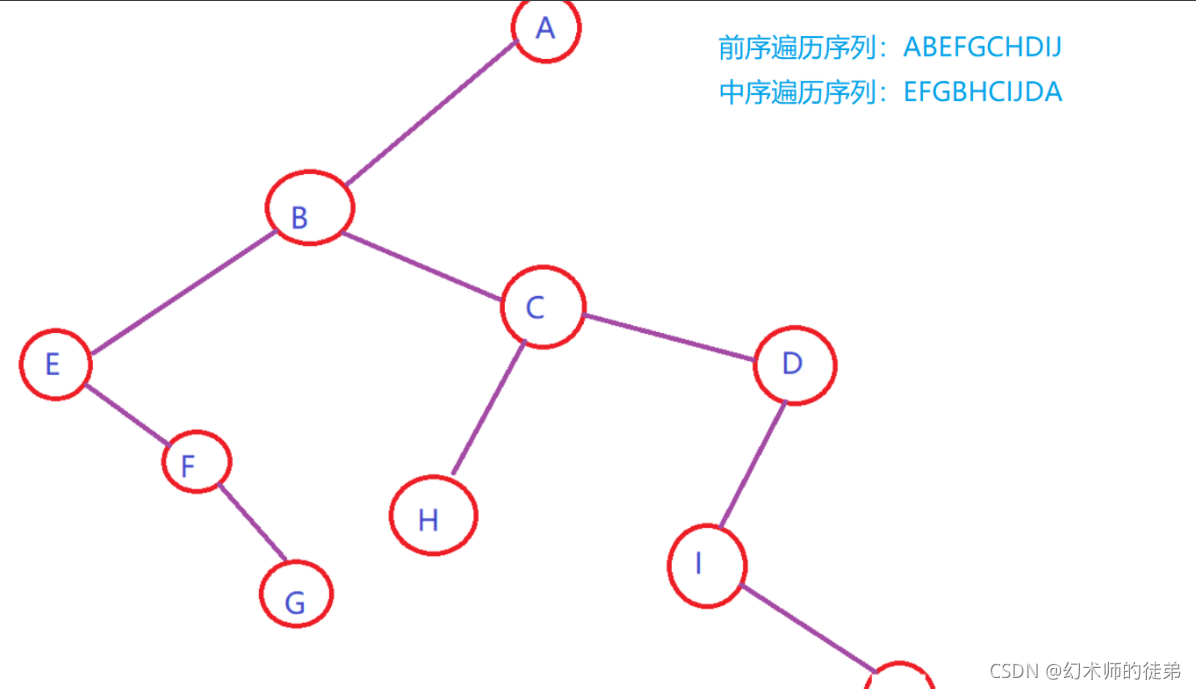
??再用一个例子说明森林的前序遍历序列等价于转化出的二叉树的前序遍历序列,森林的后序遍历序列等价于转化出的二叉树的中序遍历序列。