学习目标:
- 熟悉树的定义、表示方法、有关术语和基本概念。
- 掌握二叉树的递归定义、二叉树的性质。
- 掌握二叉树的两种存储方法、特点及适用范围。
- 掌握二叉树的各种次序的遍历。
树
1.树的定义
它是由n(n>=1)个有限节点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。(如下图)

树(tree)是包含n(n>0)个结点的有穷集,其中:
(1)每个元素称为结点(node);
(2)有一个特定的结点被称为根结点或树根(root)。
(3)除根结点之外的其余数据元素被分为m(m≥0)个互不相交的集合T1,T2,……Tm-1,其中每一个集合Ti(1<=i<=m)本身也是一棵树,被称作原树的子树(subtree)
2.树的表示方法
树形表示方法、嵌套集合表示、凹形表表示、广义表表示
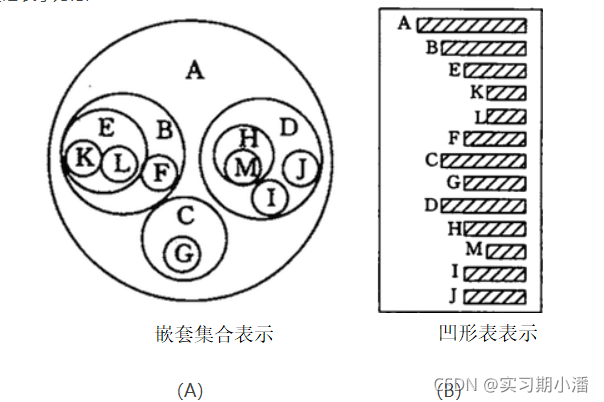

3.基本术语
为了更清晰看懂,就从下面这张图来理解

- 度:一棵树中结点的最大度数称为该树的度;
- 叶子结点(终端结点):度数为零的节点;
- 双亲(父结点):若一个节点含有子节点,则这个节点称为其子节点的父节点;
- 孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点;
- 兄弟节点:具有相同父节点的节点互称为兄弟节点;
- 节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
- 树的高度或深度:树中节点的最大层次;
- 森林:由m(m>=0)棵互不相交的树的集合称为森林;
二叉树
1.二叉树的定义
二叉树,就是度不差过2的树(节点最多有两个叉)

2.两种特殊的二叉树
-
满二叉树
一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。 -
完全二叉树
叶节点只能出现在最下层和次下层,并且最下面一层的结点都集中在该层最左边的若干位置的二叉树(只有左边有枝干)

3.二叉树的性质
- 性质1:二叉树第i层上的结点数目最多为 “2的i-1次方”个结点 (i≥1)。
- 性质2:深度为k的二叉树至多有 “2的k次方-1”个结点(k≥1)。
- 性质3:包含n个结点的二叉树的高度至少为log2 (n+1)。
- 性质4:在任意一棵二叉树中,若终端结点的个数为n0,度为2的结点数为n2,则n0=n2+1。
4.二叉树的存储方法
- 4.1 顺序存储结构(仅适用于完全二叉树)
在顺序存储一棵具有n结点的完全二叉树,只要从树根开始自上到下,每层从左至右地给该树中每个结点进行编号(假定编号从0开始),就能够得到一个反映整个二叉树结构地线性序列。

- 4.2 链式存储结构
在二叉树地链式存储表示中,通常采用地方法:每个结点设置三个域,即值域、左指针域和右指针域,用data表示值,lchild和rchild分别表示指向左右子树(孩子)地指针域。

5.二叉树地遍历
- 5.1递归遍历
递归算法定义:
a.前序遍历:根——左——右
b.中序遍历:左——根——右
c.后序遍历:左——右——根
有图来理解:
前序遍历:

遍历的结果是:GEDACHS。
中序遍历:

遍历的结果是:DEAGHCS
后序遍历:

遍历的结果是:DAEHSCG
- 5.非递归遍历
恭喜你耐着性子读完这篇博客啦~

学习建议:
茅盾在他总结自己的读书经验时说:“读名著起码要读三遍,
第一遍最好很快地把它读完,这好像在飞机上鸟瞰桂林城全景;
第二遍要慢慢地读,细细地咀嚼,注意到各章各段的结构;
第三遍要细细地一段一段地读、领会、运用,这时要注意它的炼字炼句。”