? ? ? ? 利用MATLAB完成一维搜索方法的黄金分割法、斐波那契法和二分法,为了完成作业查阅了大量资料,将其修改为了像我这种学渣差不多可以看明白的版本,同时符合老师的要求,查看时请参考下方链接,代码仅进行微改。
? ? ? ? 一维搜索方法:一维搜索,又称一维优化,是指求解一维目标函数 f(X) 最优解的过程,分为试探法和插值法。
? ? ? ? 黄金分割法:属于一维搜索方法中的试探法,适用于[a,b]区间上的任何单谷函数求极小值问题。
? ? ? ? 斐波那契(Fibonacci)法:基于斐波那契(Fibonacci)数列,关于fei数斐波那契以百度,在这就不说了。斐波那契方法是一种计算最值的方法,其基本思想类似二分法,不断缩小区间,从而实现计算最小值。
? ? ? ? 二分法:比较简单,这里不再赘述
以课本例7.1为例:
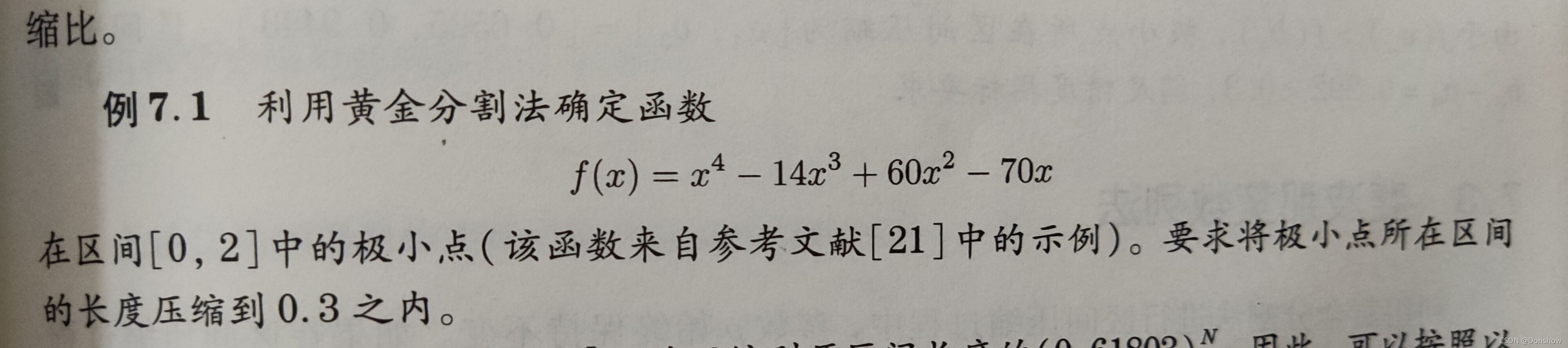
1、黄金分割法
clear all;close all;clc;
format compact
%% 定义函数和初始化
f = @(x)x^4-14*x^3+60*x^2-70*x; % 所求函数
a = 0;b = 2; % 初始搜索区间
accuracy = 0.3; % 收敛精度
r = (sqrt(5)-1)/2; % 给r赋值0.618
%% 算法部分
a1 = b - r*(b-a);
a2 = a + r*(b-a);
y1 = feval(f,a1);
y2 = feval(f,a2);
Iterations = 0; % 迭代次数初始化
%循环部分
while abs((b-a)/b) >= accuracy || abs((y2-y1)/y2) >= accuracy
Iterations = Iterations + 1;
if y1 >= y2
a = a1;
a1 = a2;
y1 = y2;
a2 = a+r*(b-a);
y2 = feval(f,a2);
else
b = a2;
a2 = a1;
y2 = y1;
a1 = b - r*(b-a);
y1 = feval(f,a1);
end
end
%% 输出
xn = (a+b)/2;
yn = feval(f,xn);
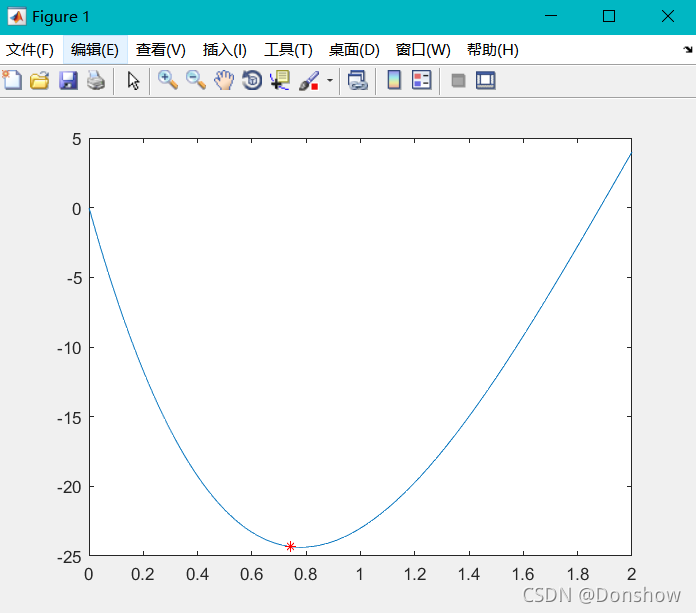
fprintf('程序经过%d次迭代得到函数极小值点为(%d,%d)\n极小点所在区间压缩为[%d,%d]',Iterations,xn,yn,a,b)
%% 绘制函数图像
x = 0:0.01:2;
y = x.*x.*x.*x-14*x.*x.*x+60*x.*x-70*x;
plot(x,y)
hold on
plot(xn,yn,'r*') % 在图像中标出极小值点运行结果:
程序经过5次迭代得到函数极小值点为(7.426458e-01,-2.432387e+01)
极小点所在区间压缩为[6.524758e-01,8.328157e-01]>>?
?2、斐波那契法
clear all;close all;clc;
format compact
%% 定义函数和初始化
f = @(x)x^4-14*x^3+60*x^2-70*x; % 所求函数
a = 0;b = 2; % 初始搜索区间
accuracy = 0.15; % 收敛精度
c = (b-a)/accuracy;
n = 1;
%% 算法部分
while fibonacci(n) < c % 确定迭代次数
n = n+1;
end
x1 = a+fibonacci(n-2)/fibonacci(n)*(b-a);
x2 = a+fibonacci(n-1)/fibonacci(n)*(b-a);
F1 = feval(f,x1);
F2 = feval(f,x2);
%%循环部分
for k=1:n-1
if F1<F2
b = x2;
x2 = x1;
F2 = F1;
x1 = a+fibonacci(n-k-2)/fibonacci(n-k)*(b-a);
F1 = feval(f,x1);
elseif F1 >= F2
a = x1;
x1 = x2;
F1 = F2;
x2 = a+fibonacci(n-k-1)/fibonacci(n-k)*(b-a);
F2 = feval(f,x2);
end
end
%% 输出
if F1<F2
b = x2;
x2 = x1;
F2 = F1;
elseif F1 >= F2
a = x1;
end
x1 = x2-0.1*(b-a);
F1 = feval(f,x1);
if F1<F2
xn = 0.5*(a+x2);
elseif F1 == F2
xn = 0.5*(x1+x2);
elseif F1>F2
xn = 0.5*(x1+b);
end
yn=feval(f,xn);
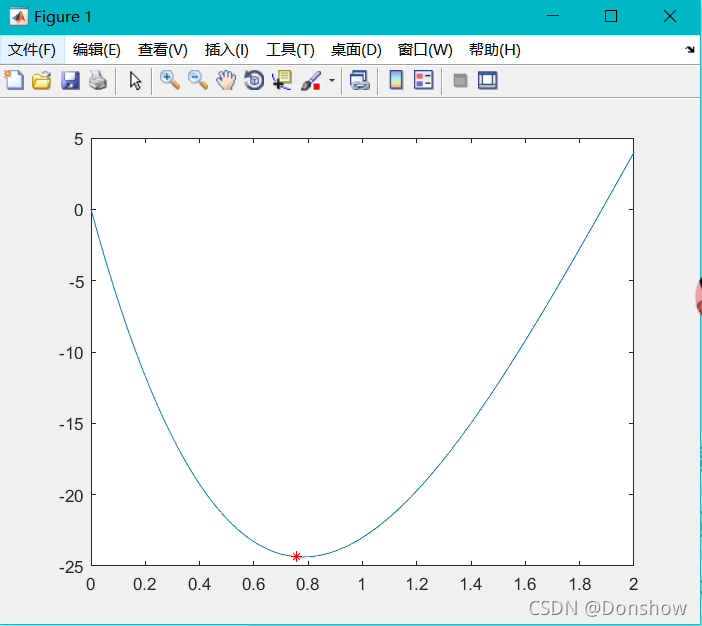
fprintf('程序经过%d次迭代得到函数极小值点为(%d,%d)\r\n',n,xn,yn)
%% 绘制函数图像
x = 0:0.01:2;
y = x.*x.*x.*x-14*x.*x.*x+60*x.*x-70*x;
plot(x,y)
hold on
plot(xn,yn,'r*') % 在图像中标出极小值点
%% 函数部分
function f=fibonacci(n)
% 用于产生斐波那契数
n=n+1;
if n>=0
a=(1+sqrt(5))/2;
b=(1-sqrt(5))/2;
c=a.^n-b.^n;
f=c/sqrt(5);
else
error('输入有误!请输入正整数(列)');
end
end运行结果:
程序经过7次迭代得到函数极小值点为(7.571429e-01,-2.435206e+01)
?3、二分法
clear all;close all;clc;
format compact
%% 定义函数和初始化
f1 = @(x)x^4-14*x^3+60*x^2-70*x; % 所求函数
f2 = @(x)4*x^3-42*x^2+120*x-70; %所求函数的一阶导数
a = 0;b = 2; % 初始搜索区间
accuracy = 0.3; % 收敛精度
fa_down = feval(f2,a);
fb_up = feval(f2,b);
n = 0;
%% 算法部分
%%循环部分
while(fa_down * fb_up < 0)
c = 0.5*(b + a);%求区间(a,b)的中点c
fc = feval(f2,c);%计算f(c)
n = n+1;
if( fc*fa_down < 0 )
b = c;% 若f(a)·f(c)<0,则令b=c
else
a = c;%若f(c)·f(b)<0,则令a=c
end
if( abs(b-a) < accuracy ) %确定区间[a,b],验证f(a)·f(b)<0,给定精确度ξ
break;
end
end
%% 输出
xn = 0.5*(b + a);
yn = feval(f1,xn);
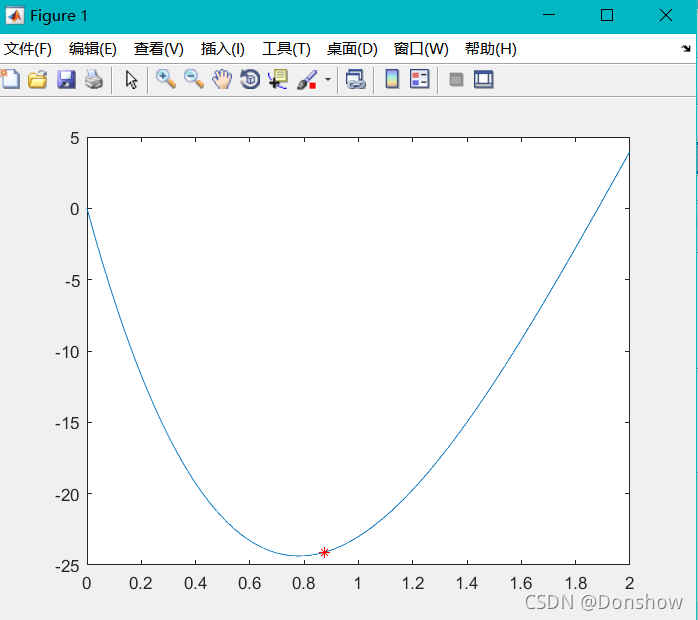
fprintf('程序经过%d次迭代得到函数极小值点为(%d,%d)\r\n',n,xn,yn)
%% 绘制函数图像
x = 0:0.01:2;
y = x.*x.*x.*x-14*x.*x.*x+60*x.*x-70*x;
plot(x,y)
hold on
plot(xn,yn,'r*') % 在图像中标出极小值点运行结果:
程序经过3次迭代得到函数极小值点为(8.750000e-01,-2.410522e+01)
?以上就是三种方法对例题的计算了,可以进行观察他们之间的差别,同时感谢各位大佬分享的知识与源代码,再次声明:以上代码改自以下三位大佬的文章,如有侵权请联系删除: