目录
决策分类树
一、决策树的介绍
分类型决策树在叶子节点上的决策规则是少数服从多数,
在一个叶子节点上,如果某一类标签所占的比例较大,那所有进入这个叶子节点的样本都回被认为是这一类别。
如果叶子节点的样本有90%都是类别0(叶子比较纯),那新进入叶子节点的测试样本的类别也很有可能是0。但是,如果51%的样本是0,49%的样本是1(极端情况),叶子节点还是会被认为是0类叶子节点,但此时此刻进入这个叶子的测试样本点几乎有一半的可能性应该是类别1。从数学上来说,类分布为(0,100%)的结点具有零不纯性,而均衡分布(50%,50%)的结点具有最高的不纯性。如果叶子本身不纯,那测试样本判断错误的概率就很大,相对的叶子越纯,那判断出错的概率就越小。
二、ID3算法构建决策树
2.1 评价指标
ID3算法的评价指标是:信息增益(Information Gain)
信息增益的计算方法可用Entropy推导,即最为人熟知的信息熵,又叫做香农熵,其计算公式如下:

其中 c 表示叶子节点上标签类别的个数,c-1 表示标签的索引。注意在这里,是从第0类标签开始计算,所以最后的标签类别应该是总共c个标签,c-1为最后一个标签的索引。在计算Entropy时设定 
2.2 案例说明
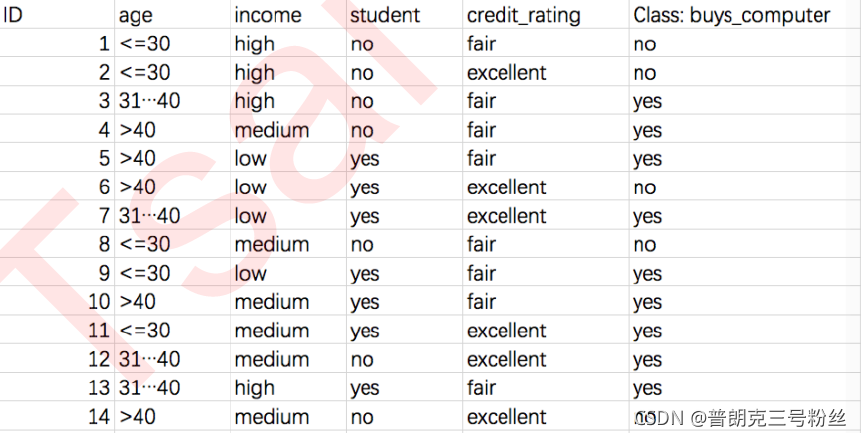
假设现在有如下数据集,是一个消费者个人属性和信用评分数据,标签是”是否会发生购买电脑行为“,这显然是个二分类问题。
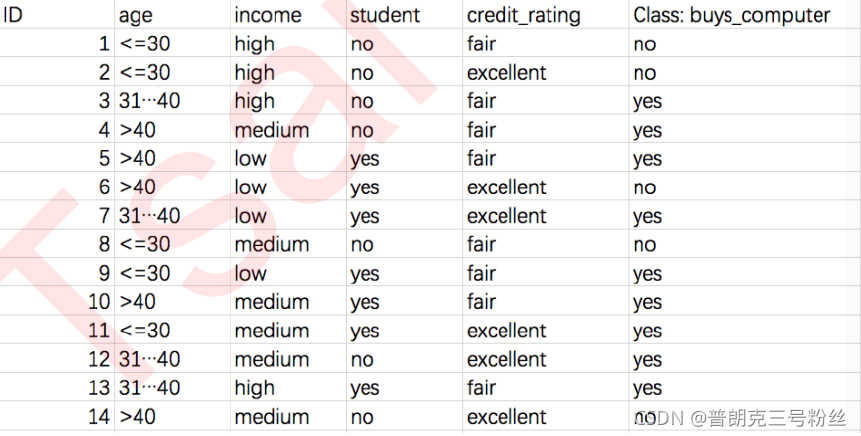
首先对于根节点而言,信息熵可用 I(s1,s2) 来表示,其中s下标1和2代表两个分类水平, 和则代表分类水平下的对应样本个数,其计算公式如下所示:

即在不进行任何切分前,总信息熵为0.940。
然后我们依次选取各特征来尝试进行切分,并计算切分完成后的子节点信息熵是多少。
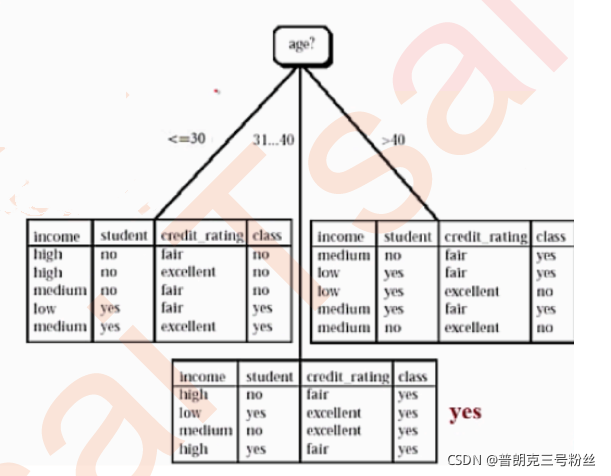
首先选取age列进行切分,age是三分类的离散变量,因此若用age对根节点进行切分,将有三个分支,每个分支分别对应一个age的取值,分支所指向的子节点为对应的切分后的数据集:
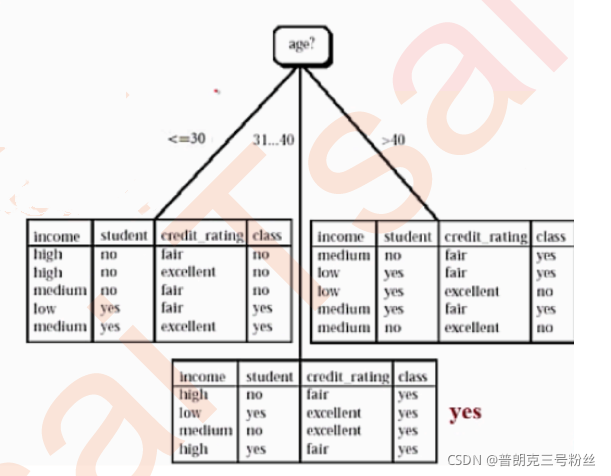
然后我们计算子节点的信息熵:
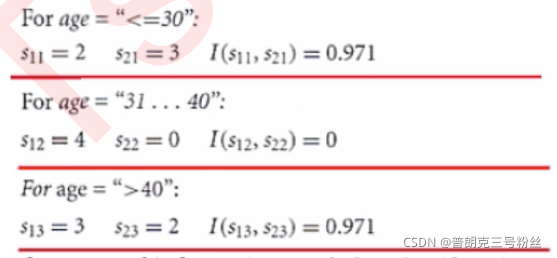
属性年龄的信息熵为:
即对于age属性而言,在根节点上切分一次之后子节点的信息熵为0.694,由此我们可计算age的信息增益,即局部最优化判别指标:

以此类推,我们还能计算其他几个特征的信息增益,最终计算结果如下Gain(income) = 0.029,Gain(student) = 0.15,Gain(credit_rating) = 0.048,很明显,第一次切分过程将采用age字段进行切分,第一次切分完成后,分成了三个数据集,其中age=“31…40"分类指标所指向的数据集纯度为1,因此不用再进行切分,而其他两个数据集则需要进一步进行切分。
age="<=30"数据集

age=">40"数据集

第一次切分完成后,分成了三个数据集,其中age=“31…40"分类指标所指向的数据集纯度为1,因此不用再进行切分,而其他两个数据集则需要进一步进行切分。
以age="<=30"的数据集为例:
I(s1,s2) = I(3,2) = -(3/5)log2(3/5) -(2/5)log2(2/5) = 0.971
在不进行任何切分前,总信息熵为0.971。
计算子节点的信息熵:
Entropy(high) = -(2/2)log2(2/2) = 0
Entropy(medium) = -(1/2)log2(1/2) - (1/2)log2(1/2)= 1
Entropy(low) = -1log2(1) = 0
计算income属性的信息熵:
Entropy(income) = (2/5)*Entropy(high)+(2/5)*Entropy(medium)+(1/5)Entropy(low) = 0.4
计算income属性的信息增益:
Gain(income) = I(s1,s2) - Entropy(income) =0.971 - 0.4= 0.571
同理,求出Entropy(Student) = 0,Entropy(credit_rating) = 0.951
得到:Gain(Student)= 0.971,Gain(credit_rating)= 0.02
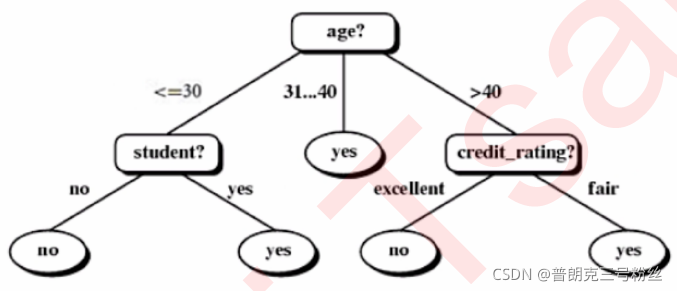
所以age="<=30"的数据集 继续以Student 属性划分下去。
同理,age=">40"的数据集则采用credit_rating字段进行切分。
最终ID3决策树模型如下所示:
2.3 ID3的局限性
不能直接处理连续型变量,若要使用ID3处理连续型变量,则首先需要对连续变量进行离散化;
对缺失值较为敏感,使用ID3之前需要提前对缺失值进行处理;
没有剪枝的设置,容易导致过拟合,即在训练集上表现很好,测试集上表现很差。
所以想在主流的决策树是由C4.5算法 & CART算法构建的。
三、C4.5算法构建决策树
3.1 评价指标
算法的评价指标是:之前的信息增益除以分支度作为选取切分字段的参考指标,该指标被称作Gain Ratio(获利比例,或增益率),计算公式如下:
其中 IV:Information Value(在《数据挖掘导论》一书中被称为划分信息度)的概念,来对信息增益的计算方法进行修正。

增益比例是我们决定对哪一列进行分枝的标准,我们分枝的是数字最大的那一列,本质是信息增益最大,分支度又较小的列(也就是纯度提升很快,但又不是靠着把类别分特别细来提升的那些特征)。IV越大,即某一列的分类水平越多,Gain ratio实现的惩罚比例越大。当然,我们还是希望GR越大越好。
3.2 案例说明
例如上个案例中,以年龄的属性来进行划分:
由于根据age字段切分后,3个分支分别有5个、4个和5个样例数据,因此age的IV指标计算过程如下:

进而可计算age列的GR:

然后可进一步计算其他各字段的GR值,并选取GR值最大的字段进行切分。
四、CART算法构建决策树
4.1 评价指标
CART算法的评价指标是 Gini?增量, 选择Gini?增量最大的属性来划分。

Gini(基尼)指数,主要用于CART决策树的不纯度判定,其计算公式如下:
4.2 案例说明
使用同一例子:
首先对于根节点而言,分裂前的基尼指数:可用 Gini(s1,s2) 来表示,其中s下标1和2代表两个分类水平, 和则代表分类水平下的对应样本个数,其计算公式如下所示:
Gini(s1,s2)= Gini(9,5)= 1-(9/14)^2 -(5/14)^2 = 0.4592
首先选取age列进行切分,age是三分类的离散变量:
当age<=30时:Gini(s11) = 1-(3/5)^2 -(2/5)^2 = 0.48;
当30<age<=40时:Gini(s12) = 1-(1)^2 = 0;
当age>40"时:Gini(s13) = 1-(3/5)^2 -(2/5)^2 = 0.48;
所以
Gini(Age) =5/14Gini(s11)+4/14Gini(s12)+5/14*Gini(s13)=0.3429
增量 = Gini(s1,s2)-Gini(Age)=0.4592-0.3429=0.1163
再分别计算出 :
Gini(s1,s2)-Gini(income);
Gini(s1,s2)-Gini(student);
Gini(s1,s2)-Gini(credit_rating)
的增量,选择增量的属性进行划分。
决策回归树
五、案例说明
下表为训练数据集,特征向量只有一维,根据此数据表建立回归决策树。

- 首先将属性的数据从小到大依此进行排列
- 然后计算俩俩相邻的数据的均值
- 按均值所在的点,对连续性变量进行二分(变成数字形式的,第一类是>均值,第二类是<均值)
- 计算指标的值,选择最佳的指标
- 选择最佳的切点进行划分
六、CART算法构建回归树
6.1 原理
在每一次划分完之后,计算均方误差MSE的值,选择误差最小的点进行划分。
MSE是真实值与预测值的差值的平方然后求和平均。

6.2 过程
- 首先将属性的数据从小到大依此进行排列,数据本身就是有序的。
- 然后计算俩俩相邻的数据的均值,一共9个切分点
{ 1.5,2.5,3.5,4.5,5.5,6.5,7.5,8.5,9.5} - 当s=1.5时,两个子区域 R_1={ 1 },
R_2={ 2,3,4,5,6,7,8,9,10 },

同理,得到其他各切分点的子区域输出值,列表如下:

- 计算损失函数值,找到最优切分点

同理,计算得到其他各切分点的损失函数值,列表如下:

易知,取s=6.5时,损失函数值最小。因此,第一个划分点为s=6.5
划分的结果为:

对于R_1,取切分点{ 1.5,2.5,3.5,4.5,5.5 },计算得到单元输出值为:

损失函数值为:

L(3.5)最小,取s=3.5为划分点。
后面同理。
七、C4.5算法构建回归树
7.1 原理
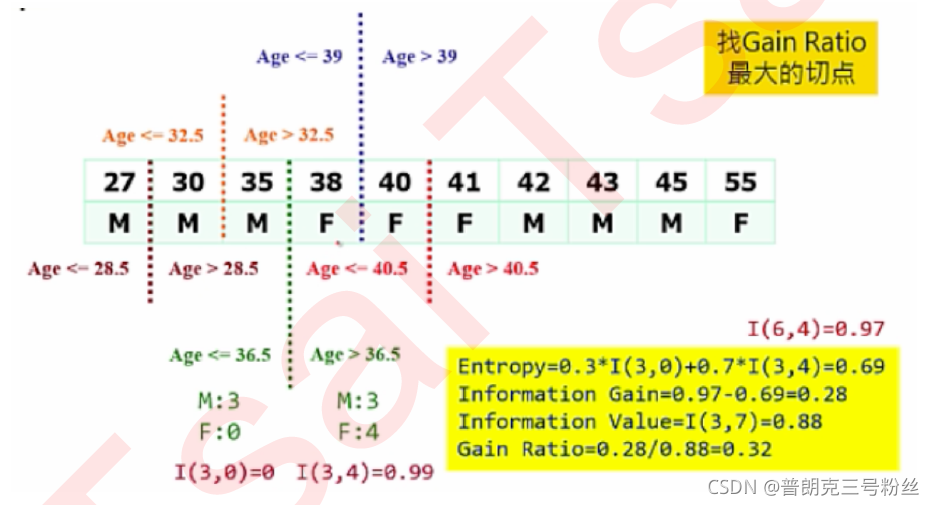
7.2 过程
除了判断标准为 Gain Ratio,其余过程与CART算法构建回归树相同。
总结
每次划分逐一考察当前集合中所有特征的所有取值,根据平方误差最小化准则选择其中最优的一个作为切分点。
这种切分方法,每次切分之后,并没有消费掉一列,只消费掉了一个备选点。在我们分类树的切分方法中,ID3每次切分就会消费掉一整个列,但实际上,我们可以只关注每次分类的时候,对信息熵的减少贡献最多的那个分类。按分类树例子来说,我们在分类age的时候,最关注的是31~40岁的那一个分类,我们完全可以实现,
31~40一类,其他算一类,然后我们再对“其他”这个类别进行相似的二分类。