[数据结构与算法]基础数据结构与算法之11种排序算法-C语言实现

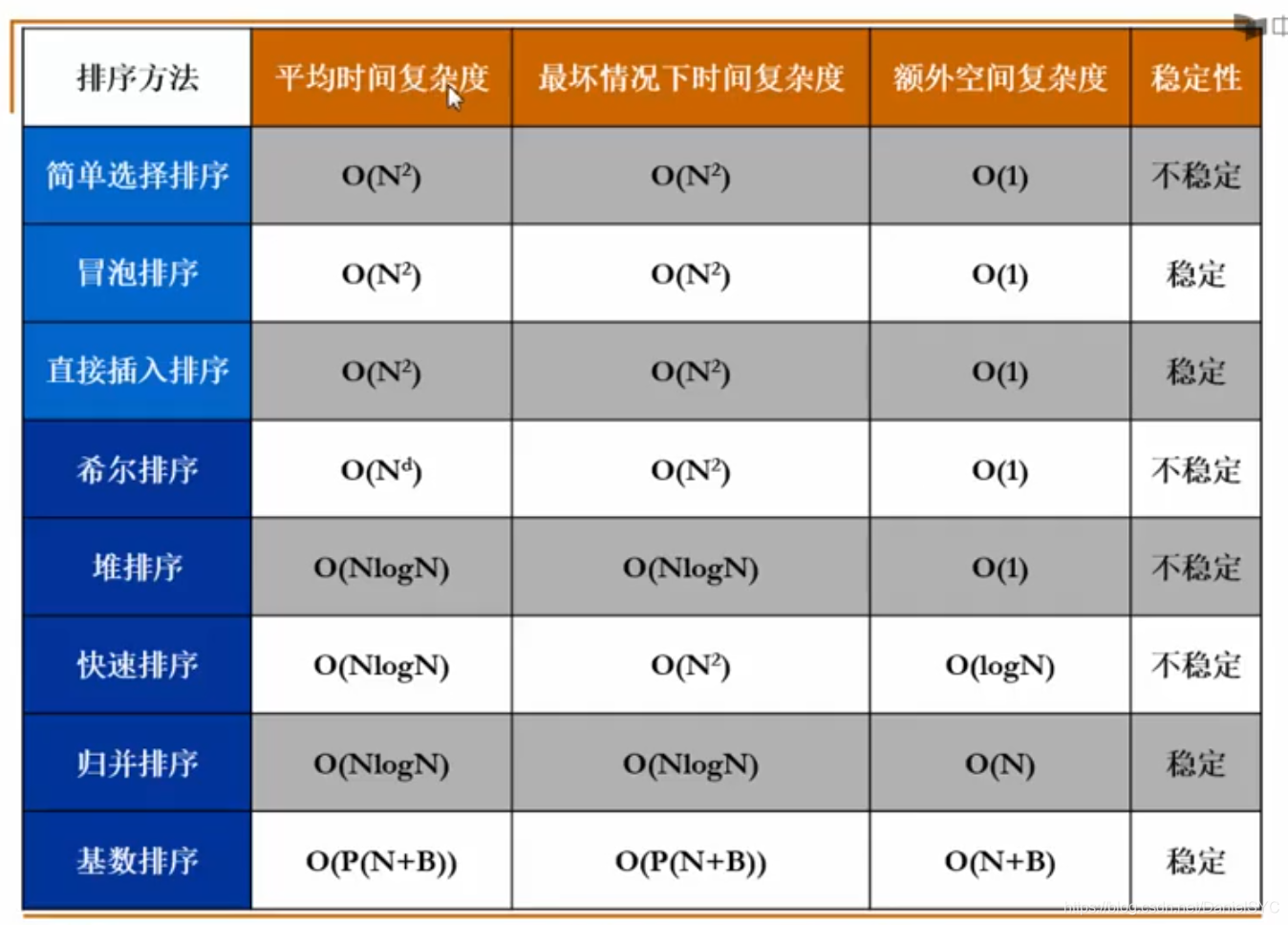
0-概述

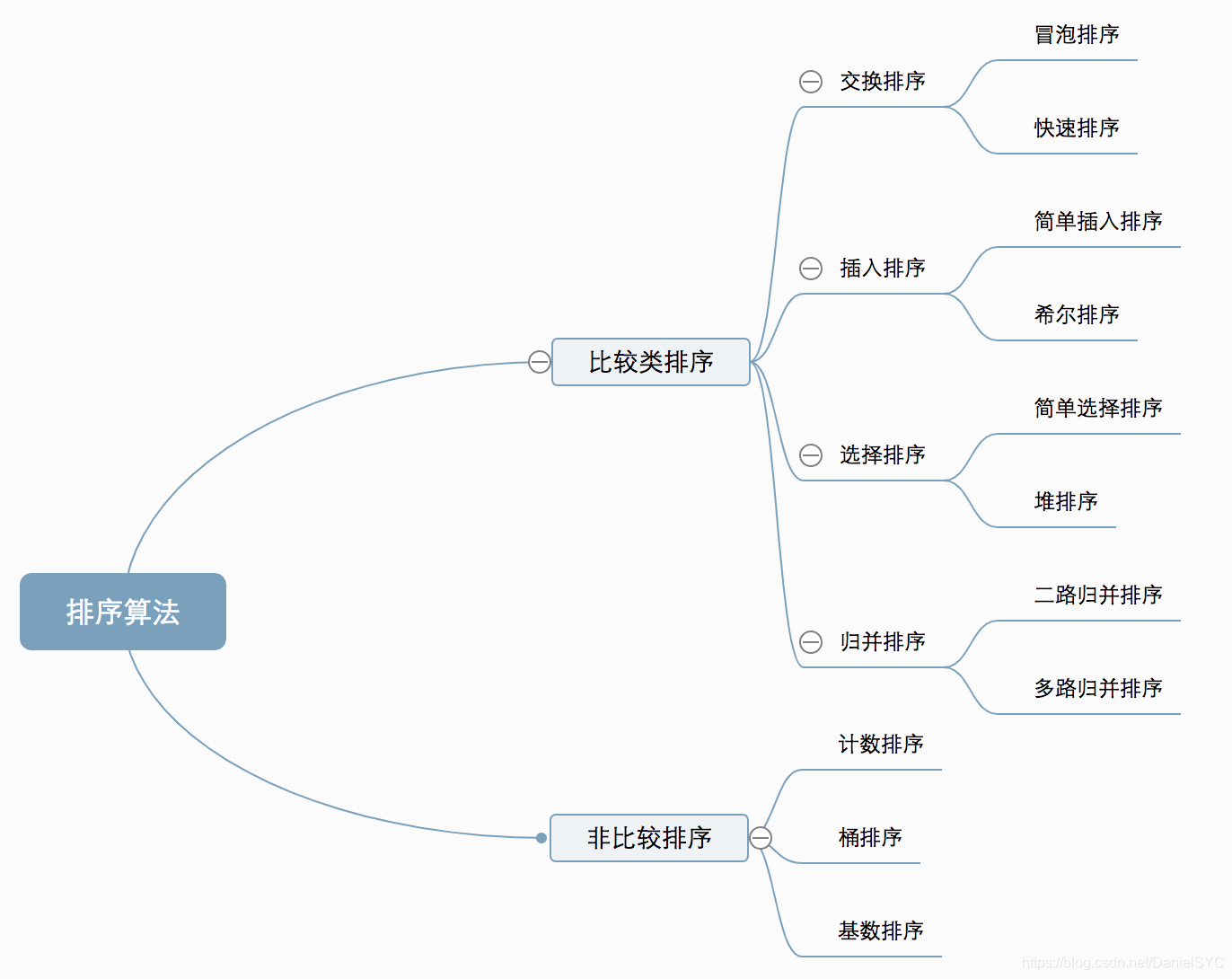
排序算法分类

常见的排序算法可以分为以下两大类：

• 比较类排序：通过比较来决定元素间的相对次序，由于其时间复杂度不能突破O(n*logn)，因此也称为非线性时间比较类排序。
• 非比较类排序：不通过比较来决定元素间的相对次序，它可以突破基于比较排序的时间下界，以线性时间运行，因此也称为线性时间非比较类排序。

对于比较类排序，其时间复杂度不能突破O(n*logn)，因为所有的比较动作可以构成一棵比较树（三叉树，每个分支对应<,=,>），N个元素的全排列数目为N!，即树中节点的个数为N!，则树高为log3(N!)，而数学上可以证明：log3(N!)=Ω(n*logn)，这就是基于比较的排序算法的时间复杂度下界。

对于非比较类排序，其可以达到线性时间复杂度，不过这一般是通过牺牲空间来换取的。

我们约定下面要讨论的排序算法的接口规范为：
void X_Sort(SortElemType A[],int N);，其中X是指排序算法的名称，并且约定：

• N是正整数，表示数组长度；
• 只讨论基于比较的排序（<,=,>有定义），而且为简单起见，只讨论从小到大的整数排序；
• 只讨论内部排序；

根据上述约定，我们的排序算法接口如下：

typedef int SortElemType;

//冒泡排序
void Bubble_Sort(SortElemType A[], int N);
//直接插入排序
void Insertion_Sort_directly(SortElemType A[], int N);
//折半插入排序
void Insertion_Sort_binary(SortElemType A[], int N);
//希尔排序
void Shell_Sort(SortElemType A[], int N);
//选择排序
void Selection_Sort(SortElemType A[], int N);
//堆排序
void Heap_Sort(SortElemType A[], int N);
//归并排序，递归版
void Merge_Sort_recursively(SortElemType A[], int N);
//归并排序，非递归版
void Merge_Sort_iteratively(SortElemType A[], int N);
//快速排序
void Quick_Sort(SortElemType A[], int N);
//计数排序
void Counting_Sort(SortElemType A[], int N);
//基数排序
void Radix_Sort(SortElemType A[], int N);

下面是一些不会提供给用户的辅助函数，只会被排序算法调用，其中有的很重要，是一些排序算法的core，而有的见名知意即可：

//交换两个数
static void swap(SortElemType* a, SortElemType* b);

//选择排序的核心：找到最小元
static int scanForMin(SortElemType* A, int begin, int end);
//堆排序的核心：向下过滤节点
static void percDown(SortElemType* A, int begin, int end);

//有序子列的归并
static void Merge(SortElemType A[], SortElemType TempA[], int L, int R, int RightEnd);
//归并排序的core
static void MSort(SortElemType A[], SortElemType TmpA[], int begin, int end);
//归并排序非递归算法核心
static void Merge_pass(SortElemType A[], SortElemType TempA[], int N, int length);
//为非递归归并排序服务的归并函数，与Merge相比，这个函数最后不会将元素倒回A中，只完成归并
static void Merge_simple(SortElemType A[], SortElemType TempA[], int L, int R, int RightEnd);

//选主元
static SortElemType Median3(SortElemType A[], int low, int high);
//划分
static int partition(SortElemType A[], int low, int high);
//快排核心
static void Quicksort(SortElemType A[], int low, int right);

//测试各种排序算法运行需要的ticks
static void testRunTime(void (*func)(SortElemType*, int), SortElemType* A, int N);
//检查数组是否已经排好序，这样就不用人工检查了
static void checkIsSorted(SortElemType A[], int N);

测试文件test.c

一个测试程序，可以通过测量排序函数运行所需的ticks（机器时钟打点数）来粗略比较各种排序算法性能的优劣。

首先从外部文件random_nums.c引入三个全局数组，里面存的是随机数，数组的size分别为200，2000，20000。

//从外部引入random_nums.c文件中的数组
extern int A_200[];
extern int A_2000[];
extern int A_20000[];

通过命令行参数指定要排序的数组（指针数组）和选用的排序算法（函数指针数组），格式如下：

$ ./x_sort 2 3
checkIsSorted:false
Selection_Sort:function ptr=0x55f266c14ccf,ticks=923723
checkIsSorted:true
$ ./x_sort 2 4
checkIsSorted:false
Heap_Sort:function ptr=0x55f17ec78d62,ticks=6165
checkIsSorted:true
./x_sort 2 5
checkIsSorted:false
Merge_Sort_recursively:function ptr=0x556822ea6e07,ticks=6550
checkIsSorted:true

第一个参数指定要排序的数组，0表示选用大小为200的随机数组A_200，1表示选用大小为2000的随机数组A_2000，2表示选用大小为20000的的随机数组A_20000。

第二个参数指定选用的排序算法，0表示冒泡排序，1表示插入排序……以此类推，具体的对应关系写在下面代码的注释中了。

主函数代码实现：

int main(int argc, char* argv[]) {
    //从外部引入random_nums.c文件中的数组
    extern int A_200[];
    extern int A_2000[];
    extern int A_20000[];
    /*
        在命令行参数中输入要选用的数组：
            0-A_200
            1-A_2000
            2-A_20000
    */
    int A_array_index = atoi(argv[1]);

    /*
        在命令行参数中输入要选用的排序算法：
            0-冒泡排序
            1-直接插入排序
            2-折半插入排序
            3-希尔排序
            4-选择排序
            5-堆排序
            6-归并排序递归版
            7-归并排序非递归版
            8-快速排序
            9-计数排序
            10-基数排序
        如果参数缺省会引发段错误，暂时就不必考虑健壮性了
    */
    int sort_algorithm_array_index = atoi(argv[2]);

    //指针数组，分别指向那三个A数组
    int* A_array[3] = {A_200, A_2000, A_20000};
    //函数指针数组，分别指向不同的排序算法函数
    void (*sort_algorithm_array[11])(SortElemType*, int);

    sort_algorithm_array[0] = Bubble_Sort;
    sort_algorithm_array[1] = Insertion_Sort_directly;
    sort_algorithm_array[2] = Insertion_Sort_binary;
    sort_algorithm_array[3] = Shell_Sort;
    sort_algorithm_array[4] = Selection_Sort;
    sort_algorithm_array[5] = Heap_Sort;
    sort_algorithm_array[6] = Merge_Sort_recursively;
    sort_algorithm_array[7] = Merge_Sort_iteratively;
    sort_algorithm_array[8] = Quick_Sort;
    sort_algorithm_array[9] = Counting_Sort;
    sort_algorithm_array[10] = Radix_Sort;

    int* A = A_array[A_array_index];
    int A_size = (int)200 * pow(10, A_array_index);

    checkIsSorted(A, A_size);
    //调用相应的函数并测量运行ticks
    testRunTime(sort_algorithm_array[sort_algorithm_array_index], A, A_size);
    checkIsSorted(A, A_size);

#ifdef PRINT_RESULT
    for (int i = 0; i < A_size; ++i) {
        printf("%d\t", A[i]);
    }
#endif

    return 0;
}

编译时需要将两个文件联编并且链接数学库，编译命令：

gcc test.c random_nums.c -o main -Wall -g -lm。如果调试时需要查看排序结果，可在编译时向程序中动态注入宏PRINT_RESULT，即添加编译选项-DPRINT_RESULT。

1-冒泡排序

算法思路

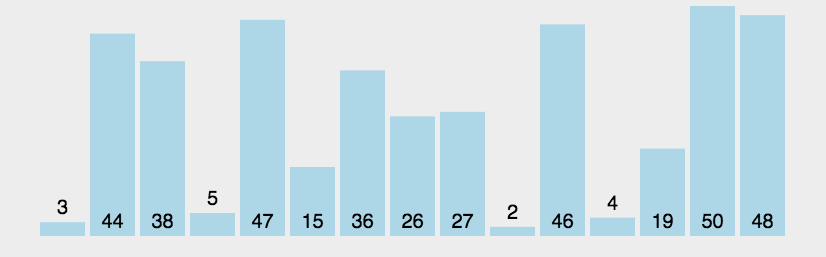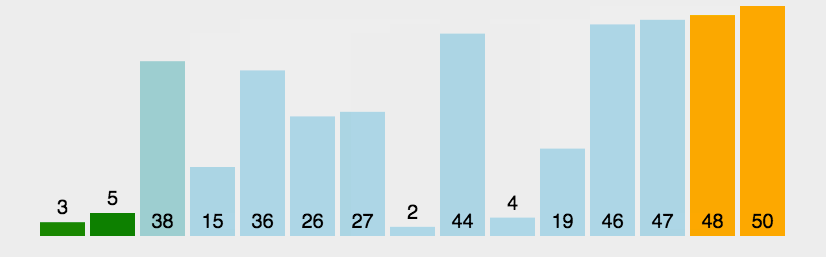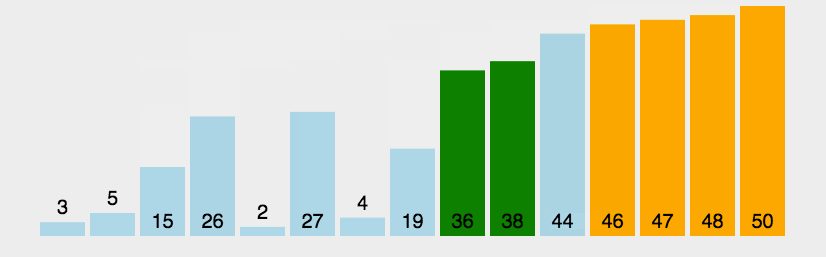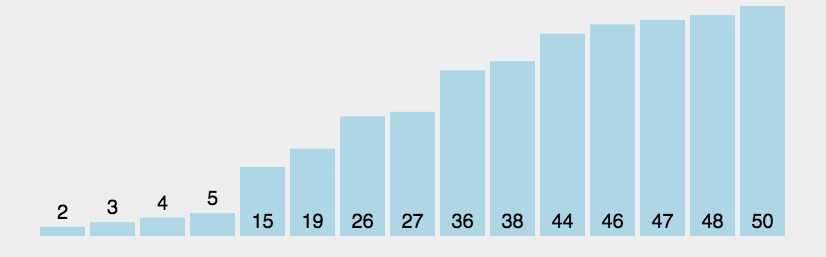
首先我们定义一个已排好序的标志int sorted=0，表示初始时未排好序；
只要!sorted，进入while循环：

1. 首先假设已经排好序：sorted=1;
2. 然后进入for循环从1开始向后扫描数组，一旦发现前面的比后面的大A[i-1]>A[i]，就交换两个数，同时sorted=0，这样，经过一轮循环，最大的元素就一定放在了最后面。
3. 将待排数组规模减一N--，进入下一次while循环。

若for循环扫描一遍后发现没有发生任何交换，说明数组已经有序sorted=1，!sorted不再满足，跳出while循环。

代码实现

void Bubble_Sort(SortElemType A[], int N) {
    printf("%s:", __func__);
    int sorted = 0;
    while (!sorted) {
        sorted = 1;
        for (int i = 1; i < N; ++i) {
            if (A[i - 1] > A[i]) {
                swap(&A[i - 1], &A[i]);
                sorted = 0;
            }
        }
        N--;
    }
    return;
}

复杂度分析

• The best time complexity=O(n);
• The worst time complexity=O(n^2);
• Space complexity=O(1);

2-直接插入排序

算法思路

初始时将待排序列第一个元素看做一个有序序列，把第二个元素到最后一个元素当成是未排序序列。

然后从头到尾依次扫描未排序序列for (p = 1; p < N; ++p)，取出未排序部分的第一个元素到tmp，并将tmp插入到前面有序序列的适当位置：i从p开始，只要i > 0 && tmp < A[i - 1]，就不断地将A[i-1]向后移动 A[i] = A[i - 1];。

跳出内层for循环时，说明tmp已经找到了合适的位置，将其插入A[i] = tmp;。

可见插入排序对于链表是比较方便的，数组还要不断的挪动空间。

代码实现

void Insertion_Sort(SortElemType A[], int N) {
    printf("%s:", __func__);
    int tmp = 0;
    int p, i;

    for (p = 1; p < N; ++p) {
        //外层循环每次取未排序部分的首个元素
        tmp = A[p];
        //从排好序的最后一个元素开始向前比较，只要tmp小，就将元素向后移
        for (i = p; i > 0 && tmp < A[i - 1]; i--) {
            A[i] = A[i - 1];
        }
        //就位
        A[i] = tmp;
    }
    return;
}

复杂度分析

• The best time complexity=O(n);
• The worst time complexity=O(n^2);
• Space complexity=O(1);

3-折半插入排序

算法思路

整体思路与直接插入排序一样，但是由于前p个元素已经有序，在前向寻找插入位置时可以采用二分查找，这样就减少了关键字的比较次数。

代码实现

void Insertion_Sort_binary(SortElemType A[], int N) {
    printf("%s:", __func__);
    int low, mid, high;
    int p;
    for (p = 1; p < N; ++p) {
        low = 0;
        high = p - 1;
        while (low <= high) {
            mid = (low + high) / 2;
            if (A[p] <= A[mid]) {
                high = mid - 1;
            } else {
                low = mid + 1;
            }
        }
        //跳出折半查找过程，low所指的位置就是待插入的位置
        int tmp = A[p];
        //将low..p的元素后移一位
        for (int j = p; j > low; --j) {
            A[j] = A[j - 1];
        }
        A[low] = tmp;
    }
}

复杂度分析

• The best time complexity=O(n);
• The worst time complexity=O(n^2);
• Space complexity=O(1);

4-希尔排序

算法思路

希尔排序是对插入排序的一种改进，其时间复杂度有所优化，但希尔排序是不稳定的。

原理概述：将无序数组分割为若干个子序列，子序列不是逐段分割的，而是相隔特定的增量的子序列，对各个子序列进行插入排序；然后再选择一个更小的增量，再将数组分割为多个子序列进行排序。最后选择增量为1，即使用直接插入排序，使最终数组成为有序。

希尔排序的效果与选用的增量序列有关，效果比较好的是Sedgewick增量序列，这里为了简单起见这里我们用N/2,N/4……来充当增量序列。

举例来说，我们有下面10个待排数据，利用for循环for (D = N >> 1; D > 0; D >>= 1)产生增量序列。首先进行D=5间隔的插入排序：

p指向增量序列的下一个元素，取到tmp中，然后向前执行插入排序，只不过把原来插入排序-1的地方都换成了-D，表示D间隔的插入排序。

然后同理进行2间隔的插入排序，最后进行1间隔的插入排序，也就是传统的插入排序，但是由于序列此时已经基本有序，执行起来要快得多。

代码实现

void Shell_Sort(SortElemType A[], int N) {
    printf("%s:", __func__);
    int D = 0;
    int tmp = 0;
    int p, i;
    // D为原始希尔序列
    for (D = N >> 1; D > 0; D >>= 1) {
        //执行D间隔的插入排序
        for (p = D; p < N; p++) {
            tmp = A[p];
            for (i = p; i >= D && tmp < A[i - D]; i -= D) {
                A[i] = A[i - D];
            }
            A[i] = tmp;
        }
    }
    return;
}

复杂度分析

• The best time complexity≈O(n^1.3);
• The worst time complexity=O(n^2);
• Space complexity=O(1);

其最好时间复杂度和平均时间复杂度与选用的增量序列有关，精确的表达式在数学上尚未得到解决。

5-选择排序

算法思路

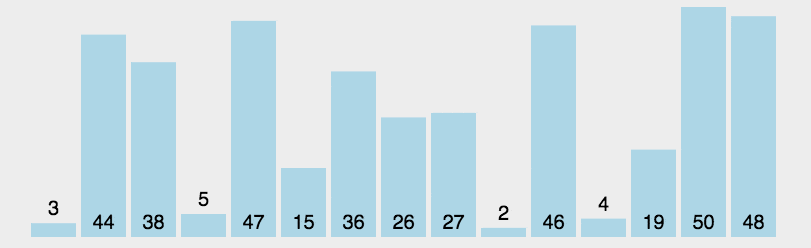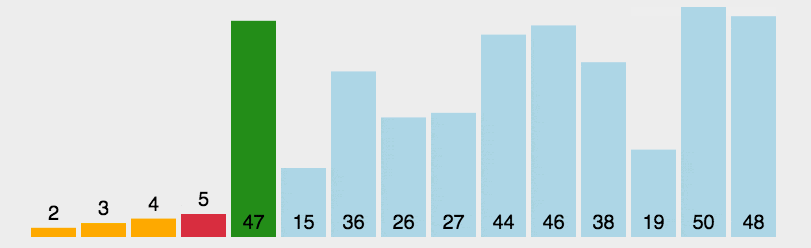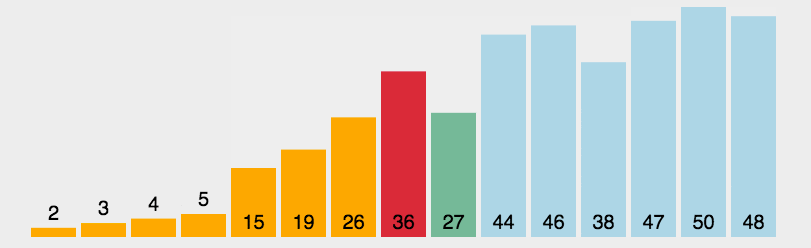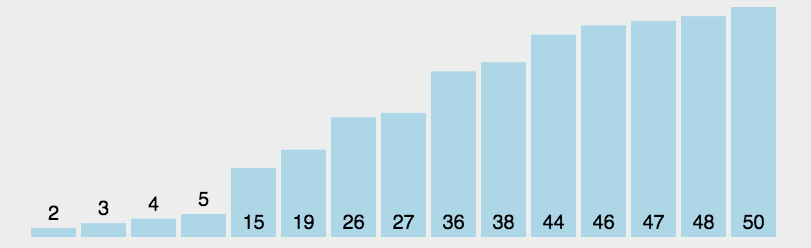
选择排序还是比较直观的：每次从未排序部分选出一个最小元，将其与未排序部分第一个元素交换即可。

代码实现

void Selection_Sort(SortElemType A[], int N) {
    printf("%s:", __func__);
    int minPositon = 0;
    for (int i = 0; i < N; ++i) {
        minPositon = scanForMin(A, i, N - 1);
        swap(&A[i], &A[minPositon]);
    }
    return;
}

其中scanForMin是寻找子列中最小元位置的函数，实现如下：

static int scanForMin(SortElemType* A, int begin, int end) {
    int minPosition = begin;
    int minElem = A[begin];
    for (int i = begin; i <= end; ++i) {
        if (A[i] < minElem) {
            minElem = A[i];
            minPosition = i;
        }
    }
    return minPosition;
}

复杂度分析

• Time complexity=O(n^2);
• Space complexity=O(1);

6-堆排序

算法思路

堆排序是对选择排序的改进。由上面选择排序的分析可知，其时间复杂度无论如何都是稳定的O(n^2)，关键在于scanForMin的时间复杂度太高，达到了O(n)，而堆排序就是利用堆的特性将scanForMin的过程优化为了O(logn)。

堆排序原理：
对于原始待排字母序列：

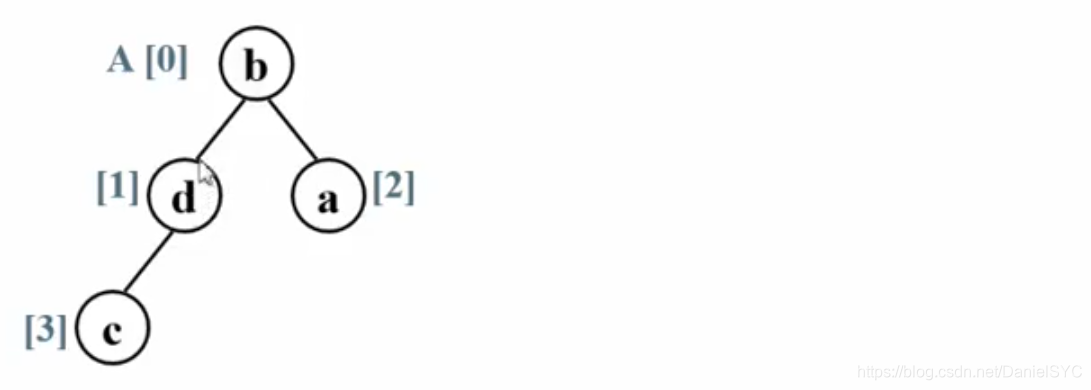
首先将其调整为一个大顶堆：

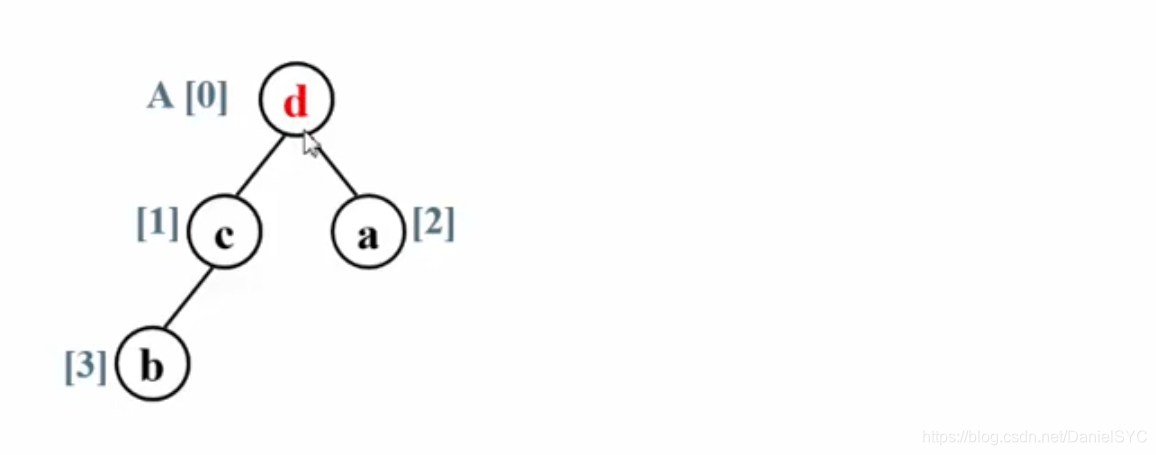
根据从小到大的排序规则，将堆顶元素（最大元素）与最后一个元素互换，这样就完成了最后一个数据的就位：

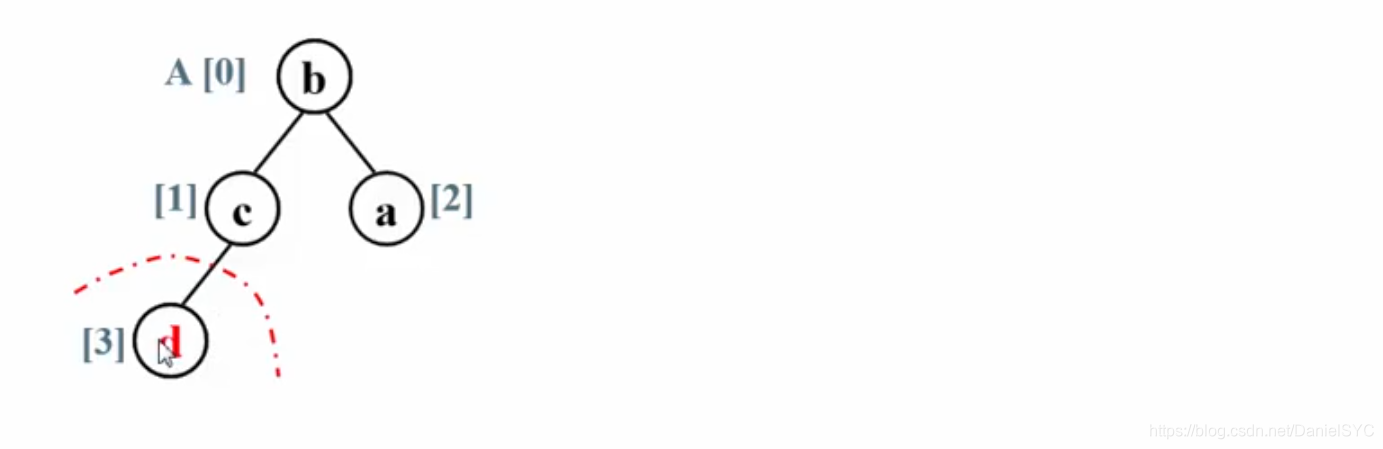
将待排数据的规模减一（红色虚线分割线），再将剩下的前三个元素调整为大顶堆：

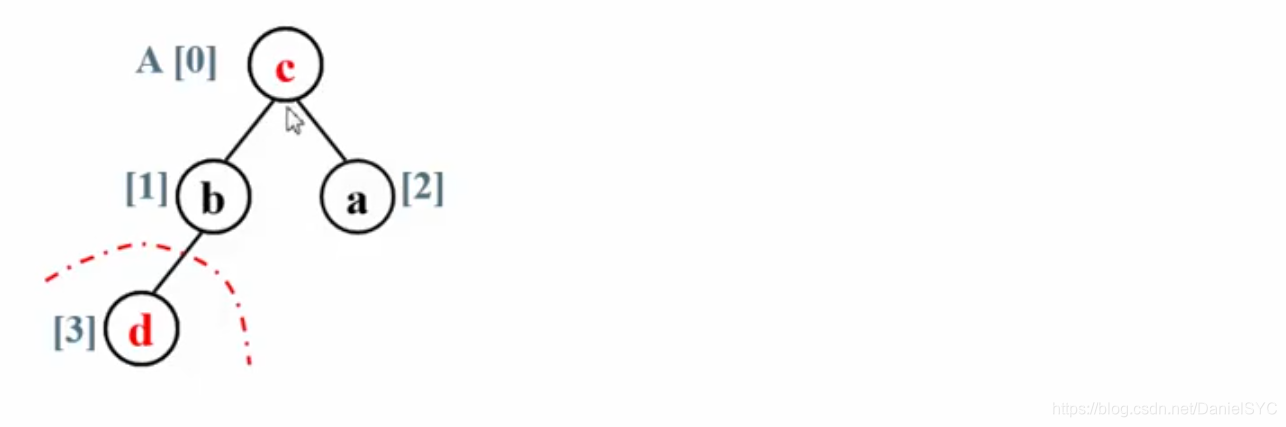
再将堆顶与最后一个元素交换位置，待排数据规模减一，这样不断进行下去，最终序列有序。

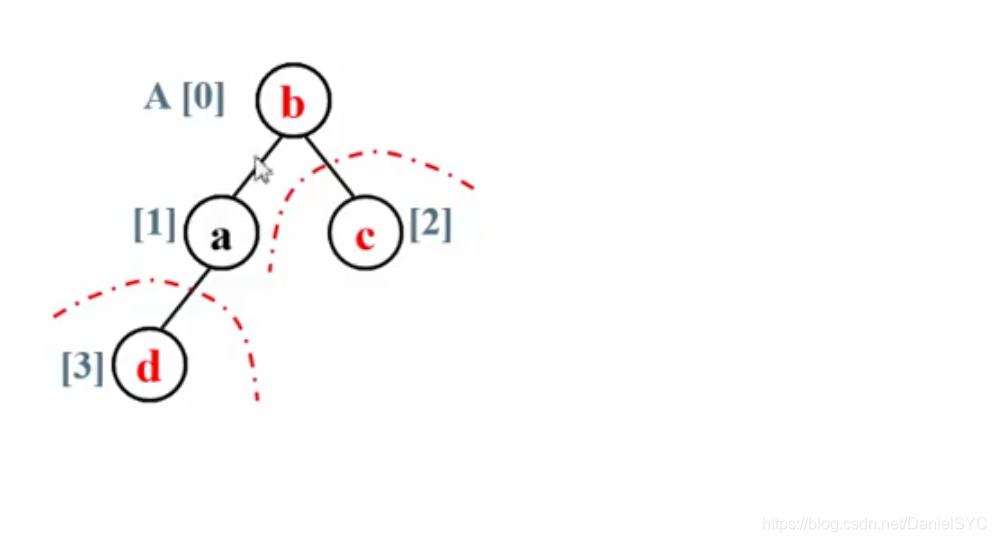
下面的动画很好地演示的堆排序的过程：

代码实现

void Heap_Sort(SortElemType A[], int N) {
    printf("%s:", __func__);
    for (int i = N / 2; i >= 0; --i) {
        percDown(A, i, N);
    }
    for (int i = N - 1; i > 0; --i) {
        swap(&A[0], &A[i]);
        percDown(A, 0, i);
    }
    return;
}

其中percDown是向下过滤节点的函数。

代码实现如下:

static void percDown(SortElemType* A, int begin, int end) {
    SortElemType top;
    int Child;
    top = A[begin];

    while (2 * begin + 1 < end) {
        Child = 2 * begin + 1;
        if ((Child != end - 1) && A[Child + 1] > A[Child]) {
            Child++;
        }
        if (top > A[Child]) {
            break;
        } else {
            A[begin] = A[Child];
            begin = Child;
        }
    }

    A[begin] = top;
}

复杂度分析

• The best time complexity=O(n*logn);
• The worst time complexity=O(n*logn);
• Space complexity=O(1);

7-归并排序-递归版

算法思路

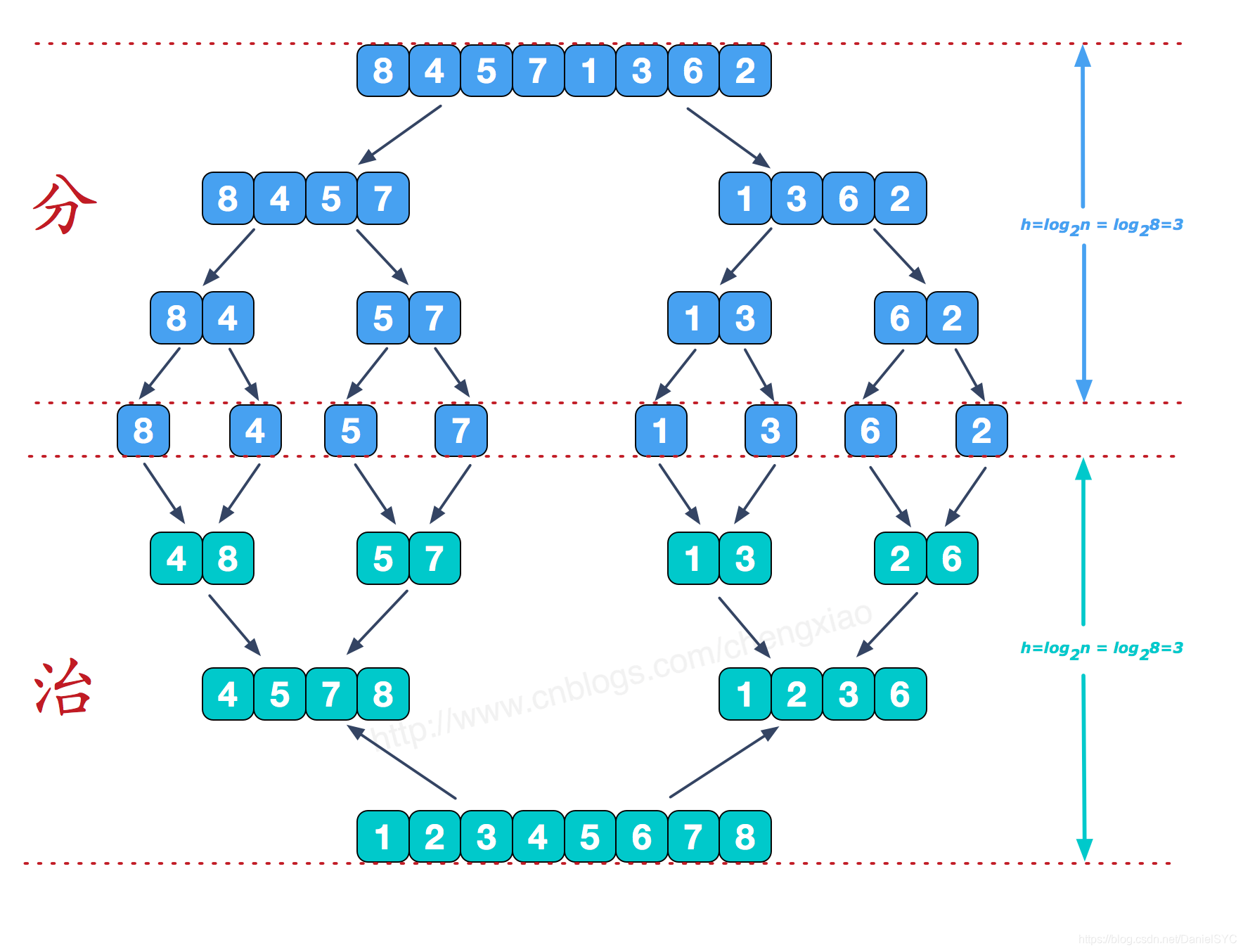
递归版本的归并排序采用分而治之的策略，每次求出待排序列的中点center = (begin + end) / 2;，然后递归地解决左半边，再递归地解决右半边，最后将从begin到center和从center+1到end的两个子列进行归并，递归终点是if (begin < end)。

下面的动画很好地演示了归并排序递归返回的过程：

代码实现

void Merge_Sort_recursively(SortElemType A[], int N) {
    printf("%s:", __func__);
    SortElemType* TmpA = malloc(N * sizeof(SortElemType));
    if (TmpA) {
        MSort(A, TmpA, 0, N - 1);
        free(TmpA);
    }
    return;
}

函数接口Merge_Sort_recursively只是申请了一个与A[]等长的辅助空间TmpA[]，然后将其传递给MSort函数进行递归排序。MSort函数实现如下，其中参数TmpA的作用就是为了最后能传递给Merge函数，在MSort函数中没有实质性用处：

static void MSort(SortElemType A[], SortElemType TmpA[], int begin, int end) {
    int center = 0;
    if (begin < end) {
        //求中点
        center = (begin + end) / 2;
        //递归的解决左半边
        MSort(A, TmpA, begin, center);
        //递归的解决右半边
        MSort(A, TmpA, center + 1, end);
        //将结果归并
        Merge(A, TmpA, begin, center + 1, end);
    }
}

Merge函数用于对两个子列进行归并，实现如下：

static void Merge(SortElemType A[], SortElemType TmpA[], int L, int R, int RightEnd) {
    //左半部分终点
    int LeftEnd = R - 1;
    //存放结果数组TmpA的起始位置
    int Tmp = L;
    //元素数目
    int NumElements = RightEnd - L + 1;
    //当左右子序列都不为空
    while (L <= LeftEnd && R <= RightEnd) {
        //将小者放入A
        if (A[L] <= A[R]) {
            TmpA[Tmp++] = A[L++];
        } else {
            TmpA[Tmp++] = A[R++];
        }
    }
    //左子序列有剩余
    while (L <= LeftEnd) {
        TmpA[Tmp++] = A[L++];
    }
    //右子序列有剩余
    while (R <= RightEnd) {
        TmpA[Tmp++] = A[R++];
    }
    //从后往前，将TmpA中的元素拷贝回A
    for (int i = 0; i < NumElements; ++i) {
        A[RightEnd] = TmpA[RightEnd];
        RightEnd--;
    }
}

复杂度分析

• Time complexity=O(n*logn);
• Space complexity=O(n);

8-归并排序-迭代版

算法思路

递归看上去比较直观，但是函数调用栈空间开销太大，优化为迭代能更好的提高效率，但是迭代版本的程序可能不好写一些（虽然说递归的程序也不好写）。

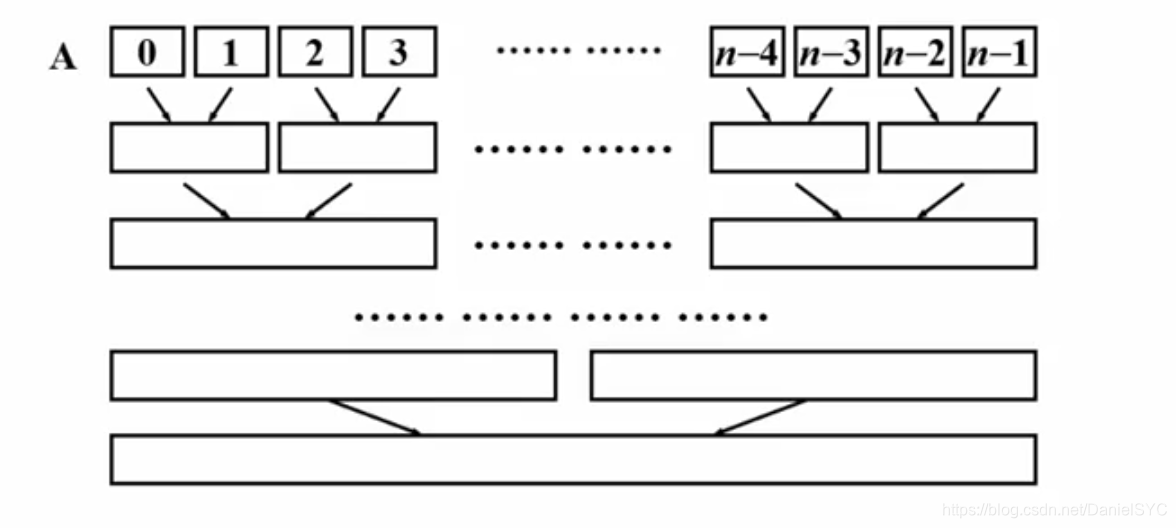
首先定义一个控制归并长度的length变量并申请与原数组等长的辅助空间TempA。

接下来进入while(length<N)循环：

• 首先进行lenght=2的归并，相当于把整个序列分割为n/2组，各组内被归并有序。

• 接着进行length=4的归并，相当于把整个序列分割为n/4组，各组内被归并有序。

• ……

• 不断的将length乘以2，直到达到N/2，将整个序列归并有序。

代码实现

void Merge_Sort_iteratively(SortElemType A[], int N) {
    printf("%s:", __func__);
    int length = 1;
    SortElemType* TempA = (SortElemType*)malloc(N * sizeof(SortElemType));
    if (TempA != NULL) {
        while (length < N) {
            Merge_pass(A, TempA, N, length);
            length *= 2;
            Merge_pass(TempA, A, N, length);
            length *= 2;
        }
        free(TempA);
    }
    return;
}

Merge_pass是用于实现一趟长度为lenght的归并的函数，在for循环中不断的调用归并函数Merge_simple(A, TempA, i, i + length, i + 2 * length - 1);，将左右两个子列进行归并，其中左起点为i，左终点为i+length-1，右起点为i+length，右终点为i+2*length-1。

注意for循环的终点是i < N - 2 * length，也就是最后会剩下一组或两组的尾巴，留作后续处理：
如果右起点i+length<N，则说明还够一趟归并的，再跑一次Merge_simple(A, TempA, i, i + length, N - 1);；
否则尾巴只剩一个左半部分了，直接追加到TempA中即可；

static void Merge_pass(SortElemType A[], SortElemType TempA[], int N, int length) {
    int i, j;
    for (i = 0; i < N - 2 * length; i += 2 * length) {
        Merge_simple(A, TempA, i, i + length, i + 2 * length - 1);
    }
    if (i + length < N) {
        Merge_simple(A, TempA, i, i + length, N - 1);
    } else {
        for (j = i; j < N; ++j)
            TempA[j] = A[j];
    }
    return;
}

见名知意，Merge_simple就是上面的Merge函数的稍微简化版，改动之处在于最后归并的结果不再倒回A中，而是直接存放在TmpA中，代码实现如下：

static void Merge_simple(SortElemType A[], SortElemType TempA[], int L, int R, int RightEnd) {
    int LeftEnd = R - 1;
    int Tmp = L;
    while (L <= LeftEnd && R <= RightEnd) {
        if (A[L] <= A[R]) {
            TempA[Tmp++] = A[L++];
        } else {
            TempA[Tmp++] = A[R++];
        }
    }
    while (L <= LeftEnd)
        TempA[Tmp++] = A[L++];
    while (R <= RightEnd)
        TempA[Tmp++] = A[R++];
    return;
}

复杂度分析

• Time complexity=O(n*logn);
• Space complexity=O(n);

9-快速排序

算法思路

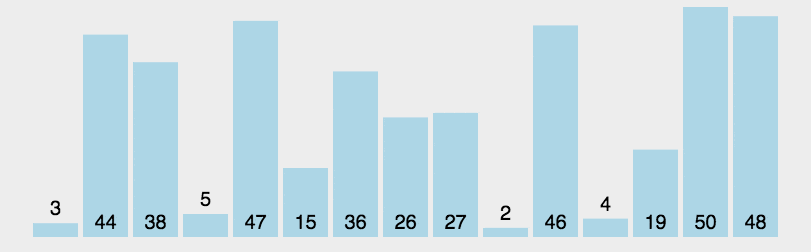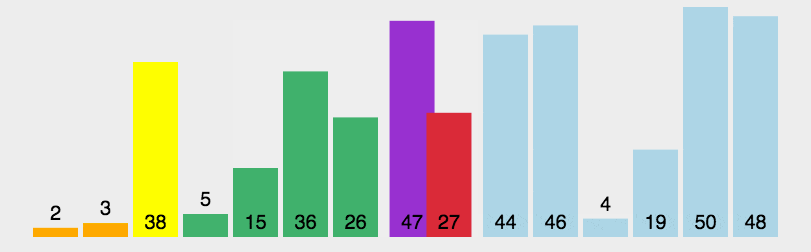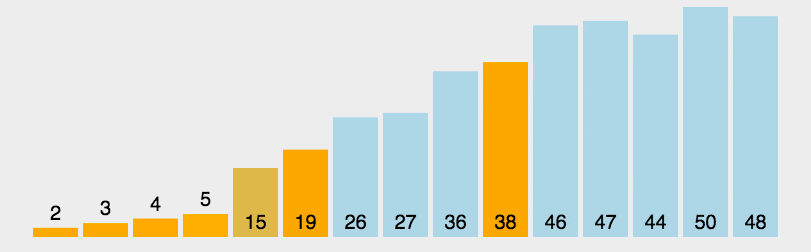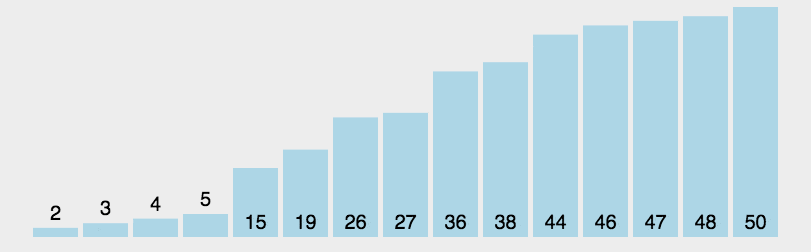
快速排序的最坏运行情况是 O(n2)，比如说顺序数列的快排。但它的平摊期望时间是 O(nlogn)，且 O(nlogn) 记号中隐含的常数因子很小，比复杂度稳定等于 O(nlogn) 的归并排序要小很多。所以，对绝大多数顺序性较弱的随机数列而言，快速排序总是优于归并排序。

算法概述：

1. 从数列中挑出一个元素，称为 “基准”（pivot）；

2. 重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作；

3. 递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序；

伪码描述如下：

值得改进的地方：

1. 对于快排函数static void Quicksort(SortElemType A[], int Left, int Right)，当数组规模较小时，为了减小递归深度，我们可以改用简单排序（如冒泡排序或插入排序等）来进行小规模数据的排序。例如我们可以设定一个阈值cutOff=100，当待排数组长度high - low小于阈值cutOff时，就使用简单排序。
2. 主元的选定matters，如果我们每次都能选定序列的中位数作为pivot，就能达到最好的时间复杂度。这里我们选择了待排数组的头、中、尾这三个数的中位数进行近似。

代码实现

因为Quicksort函数是递归调用的，所以这里的Quick_Sort只是为了提供给用户统一的接口而对核心Quicksort函数进行了封装。

void Quick_Sort(SortElemType A[], int N) {
    printf("%s:", __func__);
    Quicksort(A, 0, N - 1);
    return;
}

快排的核心：

static void Quicksort(SortElemType A[], int low, int high) {
    static const int cutOff = 100;
    if (high - low > cutOff) {
        int pivotPosition = partition(A, low, high);
        Quicksort(A, low, pivotPosition - 1);
        Quicksort(A, pivotPosition + 1, high);
    } else {
        SortElemType* smallArray = A + low;
        int N = high - low + 1;
        int sorted = 0;
        while (!sorted) {
            sorted = 1;
            for (int i = 1; i < N; ++i) {
                if (smallArray[i - 1] > smallArray[i]) {
                    swap(&smallArray[i - 1], &smallArray[i]);
                    sorted = 0;
                }
            }
            N--;
        }
    }
    return;
}

划分：

static int partition(SortElemType A[], int low, int high) {
    int pivot = Median3(A, low, high);
    while (low < high) {
        while (low < high && A[high] >= pivot) {
            high--;
        }
        A[low] = A[high];
        while (low < high && A[low] <= pivot) {
            low++;
        }
        A[high] = A[low];
    }
    A[low] = pivot;
    return low;
}

选主元：
经过三个if判断后，Left，Center，Right就从小到大有序了，最后将主元返回。

static SortElemType Median3(SortElemType A[], int low, int high) {
    int center = (low + high) / 2;
    if (A[low] > A[center]) {
        swap(A + low, A + center);
    }
    if (A[low] > A[high]) {
        swap(A + low, A + high);
    }
    if (A[center] > A[high]) {
        swap(A + center, A + high);
    }

    return A[center];
}

复杂度分析

• The best time complexity=O(n*logn);
• The worst time complexity=O(n^2);
• Space complexity=O(logn);

10-计数排序

算法思路

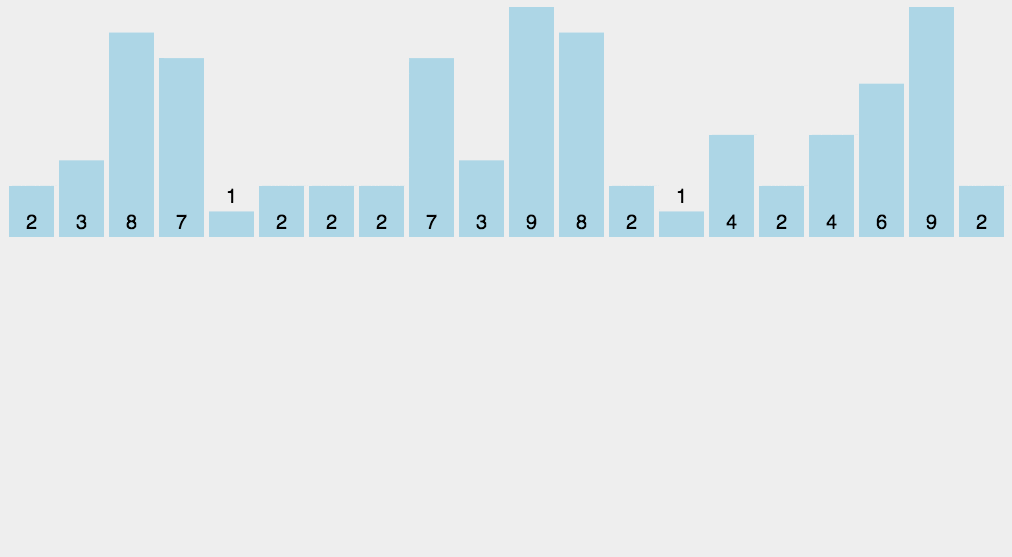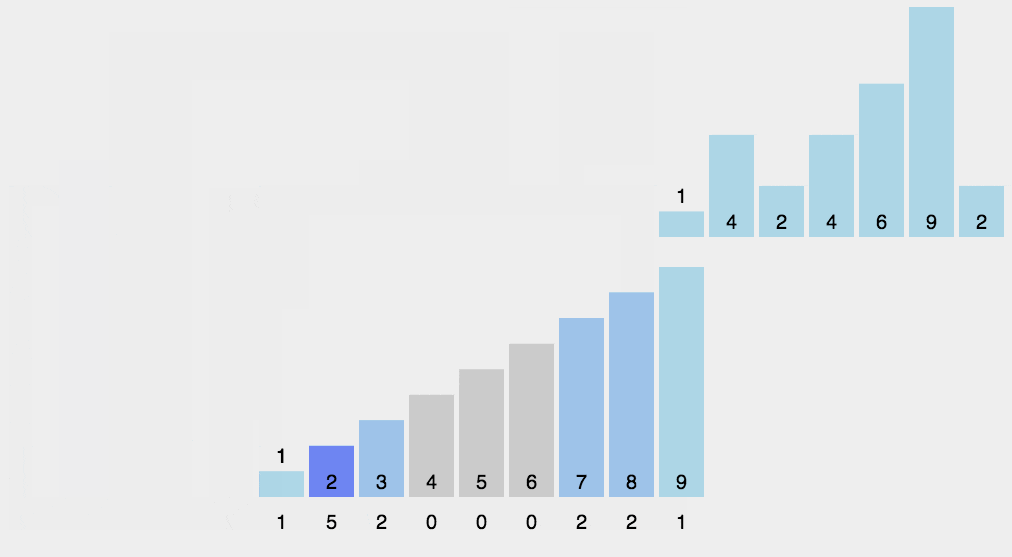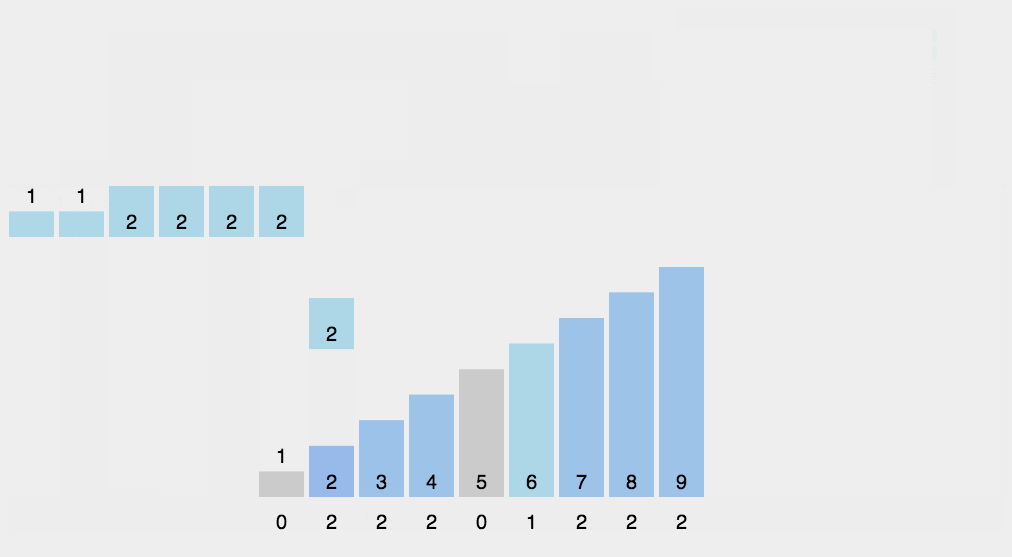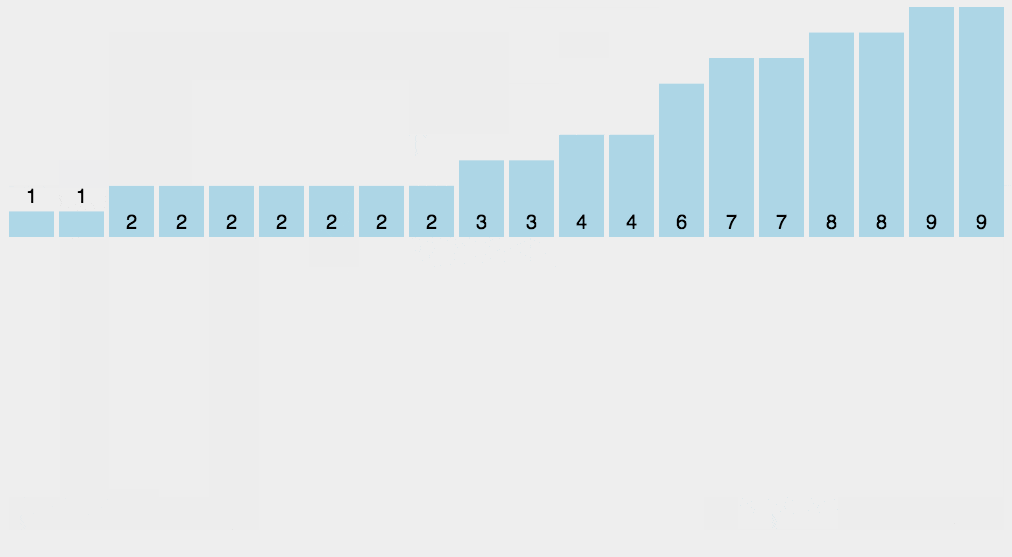
作为一种基于非比较类的排序，计数排序的的时间复杂度为O(n)，但这是以牺牲空间为代价的，其空间复杂度为O(n+max)，与数组中最大元素的值有关。

1. 首先遍历一遍数组找到其最大值存入max中。
2. 接着开辟一个max大小的辅助空间，也就是桶bucket。
3. 接着遍历待排数组，将其每个元素A[i]看做bucket的下标，执行bucket[A[i]]++。如果将数组看成一种map映射的话，其下标相当于key，数组元素值相当于value，遍历完成后，bucket中就存储了A中每个元素出现的次数。
4. 最后从0到max遍历bucket，利用bucket中保存的数组元素的出现次数的信息形成已排序数组。

代码实现

void Counting_Sort(SortElemType A[], int N) {
    printf("%s:", __func__);
    SortElemType max = A[0];
    for (int i = 1; i < N; ++i) {
        if (A[i] > max)
            max = A[i];
    }
    SortElemType* bucket = (SortElemType*)malloc(sizeof(SortElemType) * max);
    memset(bucket, 0, max);
    if (bucket != NULL) {
        for (int i = 0; i < N; ++i) {
            bucket[A[i]]++;
        }
        for (int i = 0, j = 0; i <= max; ++i) {
            while ((bucket[i]--) > 0)
                A[j++] = i;
        }
        free(bucket);
        return;
    } else {
        printf("空间不足\n");
        return;
    }
}

复杂度分析

• Time complexity=O(n);
• Space complexity=O(n+max);

11-基数排序

算法思路

1. 遍历序列找出最大的数max，并确定其位数digit_num；

2. 开辟一个与数组A大小相同的临时数组temp；

3. 进入外层对每一数位进行处理的循环for (i = 1; i <= digit_num; ++i, radix *= 10;)；

4. 用一个count数组统计原数组中某一位（从低位向高位统计）相同的数据出现的次数；

5. 对count数组进行递推累加，这样，count中的每个count[i]都保存了从count[0]到count[i]的和；

6. 最后和计数排序一样，利用count中保存的数组元素的出现次数的信息形成已排序数组temp。

7. 将tmep数组拷回到原数组中，进入下一轮每一数位进行处理的循环；

代码实现

void Radix_Sort(SortElemType A[], int N) {
    printf("%s:", __func__);
    SortElemType max = A[0];
    for (int i = 1; i < N; ++i) {
        if (A[i] > max)
            max = A[i];
    }
    int digit_num = 0;
    while (max) {
        max /= 10;
        digit_num++;
    }

    SortElemType count[10];
    SortElemType* temp = (SortElemType*)malloc(sizeof(SortElemType) * N);
    int i, j, k;
    int radix = 1;
    for (i = 1; i <= digit_num; ++i, radix *= 10) {
        memset(count, 0, 10 * sizeof(SortElemType));
        for (j = 0; j < N; ++j) {
            k = (A[j] / radix) % 10;
            count[k]++;
        }
        for (j = 1; j < 10; ++j) {
            count[j] = count[j - 1] + count[j];
        }
        for (j = N - 1; j >= 0; j--) {
            k = (A[j] / radix) % 10;
            temp[count[k] - 1] = A[j];
            count[k]--;
        }
        //将temp中的元素倒回A
        for (j = 0; j < N; ++j) {
            A[j] = temp[j];
        }
    }
    
    free(temp);
}

复杂度分析

• Time complexity=O(n);
• Space complexity=O(n);

11-测试函数运行时间

第一个参数为指向不同排序算法的函数指针*func，后两个参数为待排数组A和数组长度N，也就是*func的参数。

static void testRunTime(void (*func)(SortElemType*, int), SortElemType* A, int N) {
    clock_t start, stop;
    start = clock();
    (*func)(A, N);
    stop = clock();
    printf("function ptr=%p,ticks=%ld\n", func, stop - start);
}

12-检查数组是否已经排好序

static void checkIsSorted(SortElemType A[], int N) {
    for (int i = 1; i < N; ++i) {
        if (A[i - 1] > A[i]) {
            printf("%s:false\n", __func__);
            return;
        }
    }
    printf("%s:true\n", __func__);
    return;
}

13-各种排序算法的比较