文章目录
十大排序算法
参考文章
概要:算法时间复杂度
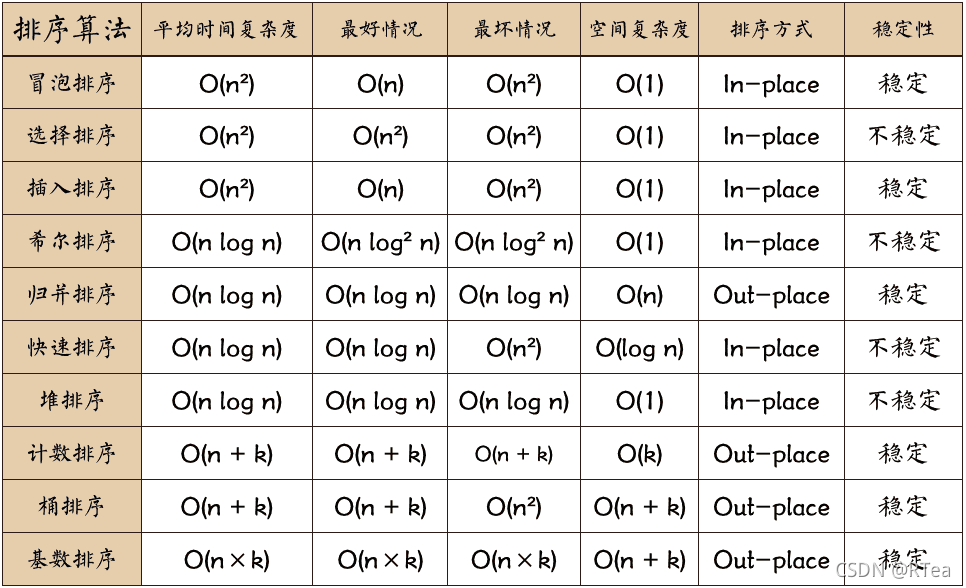
复杂度计算
关键理解:O(log(n)),2^t=n即循环t次后≤n
void main() {
int i=1;
int n=100;
while(i<n) {
i = i*2;
}
}
O(nlog(n))即n次的O(log(n))循环
时间复杂度对比:O(1 )< O(logn) < O(n) < O(n*logn) < O(n2)< O(n3) < O(2^n) < O(n!) < O(n^n)
具体算法
1.冒泡排序
1.1 概要
每轮遍历逆序时,获得最大值,类似冒水泡一样向上变大
1.2 代码
public int[] bubbleSort(int[] array){
int len = array.length;
for(int i=len-1; i>0; i--){
for(int j=0; j<i; j++){
if(array[j] > array[j+1]){
swap(array, j, j+1);
}
}
}
return array;
}
1.3 优化
加标志flag,遍历判断有序后,不必之后再遍历
1.4 时间复杂度
最优:顺序排序O(n)
最差:逆序排序O(n^2)
2.选择排序
2.1 概要
每轮选最小的排序
2.2 代码
public int[] selectionSort(int[] array){
for(int i=0; i<array.length; i++){
int minIdx = i;
for(int j=i+1; j<array.length; j++){
if(array[minIdx] > array[j]){
swap(array, minIdx, j);
}
}
}
return array;
}
2.3 时间复杂度
O(n^2)
3. 插入排序
3.1 概要
扑克牌:每轮选出较小的往前面挪(前面已有序)
3.2 代码
public int[] insertionSort(int[] nums){
for(int i=1; i<nums.length; i++){
// 记录需要做比较相邻前面的“牌”
int pre = i;
// 保存需要插入的“牌”
int value = nums[i];
while(pre > 0 && value < nums[pre-1]){
nums[pre] = nums[pre-1];
pre--;
}
// “牌”交换过位置,插牌
if(pre != i){
nums[pre] = value;
}
}
return nums;
}
3.3 时间复杂度
最优复杂度:O(n)
最差复杂度:O(n^2)
4 希尔排序
4.1 概要
缩小增量排序
4.2 代码
public int[] shellSort(int[] arr){
//增量gap,并逐步缩小增量。初始选择长度/2
for(int gap=arr.length/2;gap>0;gap/=2){
//从gap位元素开始,以gap为步距跳跃尝试交换
for(int i=gap;i<arr.length;i++){
int j = i;
while(j-gap>=0 && arr[j]<arr[j-gap]){
//插入排序采用交换法
swap(arr,j,j-gap);
j-=gap;
}
}
}
return arr;
}
4.3 时间复杂度
平均时间复杂度:O(nlogn)
最坏时间复杂度:O(n^2)
5 归并排序
5.1 概要
秉承“分治”思想,先把数组分割成小块,再比较每一对小块且合并成原来数组
5.2 代码
public void mergeSort(int[] nums, int l, int r){
if(l == r){
return;
}
int m = (l+r)/2;
// 递归分割数组成小块
mergeSort(nums, l, m);
mergeSort(nums, m+1, r);
// 比较合并小块
mergeTwoArrays(nums, l, m+1, r);
}
public void mergeTwoArrays(int[] nums, int l, int m, int r){
int[] leftArray = new int[m-l];
int[] rightArray = new int[r-m+1];
leftArray = Arrays.copyOfRange(nums, l, m);
rightArray = Arrays.copyOfRange(nums, m, r+1);
int li = 0, rj = 0;
int idx = l;
while(li < leftArray.length && rj < rightArray.length){
if(leftArray[li] < rightArray[rj]){
nums[idx++] = leftArray[li++];
}else {
nums[idx++] = rightArray[rj++];
}
}
while(li < leftArray.length){
nums[idx++] = leftArray[li++];
}
while(rj < rightArray.length){
nums[idx++] = rightArray[rj++];
}
}
5.3 时间复杂度
平均时间复杂度:O(nlogn)
最差时间复杂度:O(nlogn)
6 快速排序
6.1 概要
取基准(基准两侧分别是较小数和较大数),再递归取左右两侧的基准(分治)
6.2 代码
// 取基准分割数组,左边比基准小,右边比基准大
public void quickSort(int[] nums, int l, int r){
if(l < r){
int pos = partition1(nums, l, r);
quickSort(nums, l, pos-1);
quickSort(nums, pos+1, r);
}
}
public int partition1(int[] nums, int l, int r){
int value = nums[l];
while(l < r){
// 比较右边
while(nums[r] > value && l < r) r--;
nums[l] = nums[r];
// 比较左边
while(nums[l] < value && l < r) l++;
nums[r] = nums[l];
}
nums[l] = value;
return l;
}
6.3 时间复杂度
平均时间复杂度:O(nlogn)
最差时间复杂度:O(n^2) 顺序数列则慢
7 堆排序
7.1 概要
- 构建大顶堆
- 交换堆顶元素和末尾元素
关键:
- 构建大顶堆时,需要自下到上从第一个非叶子节点(nums.length/2-1)开始
- 顺序改变后需要调整子树
7.2 代码
public void heapSort(int[] nums){
// 1 构建大顶堆
// 从第一个非叶子节点开始与左右节点交换(从下到上,从右到左)
for(int i=nums.length/2 - 1; i>=0; i--){
adjustHeap(nums, i, nums.length);
}
// 2 调整堆结构,堆顶与末尾元素交换
for(int j=nums.length-1; j>0; j--){
swap(nums, 0, j);
adjustHeap(nums, 0, j);
}
}
public void adjustHeap(int[] nums, int i, int length){
// 左右子树
int l = i * 2 + 1, r = i * 2 + 2, parent = i;
if(l < length && nums[l] > nums[parent]) parent = l;
if(r < length && nums[r] > nums[parent]) parent = r;
// 证明顺序改变,需要调整子树
if(parent != i){
swap(nums, parent, i);
adjustHeap(nums, parent, length);
}
}
7.3 时间复杂度
平均时间复杂度:O(nlogn)
最差时间复杂度:O(nlogn)
8 计数排序
8.1 概要
新建数组的索引下标存待排序数组数字出现的次数,遍历输出新数组
关键:注意特大数字占用空间过大问题
8.2 代码
// 选取最大的数,新建数组用index保存nums的出现次数
// 遍历数组,按顺序输出即可
public int[] countingSort(int[] nums){
int bucketLen = getMaxCount(nums);
int[] countArray = new int[bucketLen+1];
for(int i=0; i<nums.length; i++){
countArray[nums[i]]++;
}
int[] res = new int[nums.length];
int resIdx = 0;
for(int j=0; j<=bucketLen; j++){
while(countArray[j]-- > 0){
res[resIdx++] = j;
}
}
return res;
}
public int getMaxCount(int[] nums){
return Arrays.stream(nums).max().getAsInt();
}
8.3 时间复杂度
平均时间复杂度:O(n+k)
最差时间复杂度:O(n+k)
9 桶排序
9.1 概要
先规定每个桶的大小;
再计算桶的个数 bucketCount = (max - min) / bucketSize + 1;
根据 (nums[i] - min) / bucketSize 分配数字进桶;
分别为每个桶排序;
最后输出每个桶的数字
9.2 代码
public List<Integer> bucketSort(int[] nums, int bucketSize){
int max = nums[0];
int min = nums[0];
for(int i=0; i<nums.length; i++){
max = max > nums[i] ? max : nums[i];
min = min < nums[i] ? min : nums[i];
}
// 桶数量
int bucketCount = (max - min) / bucketSize + 1;
List<List<Integer>> buckets = new ArrayList<>();
for(int i=0; i<bucketCount; i++){
buckets.add(new ArrayList<>());
}
// 数字分配进桶
for(int i=0; i<nums.length; i++){
buckets.get((nums[i]-min)/bucketSize).add(nums[i]);
}
List<Integer> res = new ArrayList<>();
for(int i=0; i<bucketCount; i++){
buckets.get(i).sort(null);
buckets.get(i).stream().forEach(e -> res.add(e));
}
return res;
}
9.3 时间复杂度
平均时间复杂度:O(n+k)
最坏时间复杂度:O(n^2)
10 基数排序
10.1 概要
从低位到高位,每次按照当前位排序,当前位没有的数字补0(这样每次排序就会在第一位)
排序到最后一位输出
10.2 代码
/**
* 每次排序数组中数字位
* @param nums
*/
public int[] radixSort(int[] nums){
int loopNum = getMaxNumDigits(nums);
List<Integer>[] tmp = new ArrayList[10];
int[] radix = new int[nums.length];
for(int i=0; i< nums.length; i++){
radix[i] = nums[i];
}
for(int i=1; i<=loopNum; i++){
// 初始化基数排序数组
for(int m=0; m<10; m++){
tmp[m] = new ArrayList<>();
}
// 排序,遇到不足位数的补0
for(int j=0; j<radix.length; j++){
tmp[getNthNum(radix[j], i)].add(radix[j]);
}
// 把基数排序的数组重新捋顺到一维数组中
int idx = 0;
for(int k=0; k<10; k++){
for(int l=0; l<tmp[k].size(); l++){
radix[idx++] = tmp[k].get(l);
}
}
}
return radix;
}
public int getNthNum(int num, int n){
if (n == 1) {
return num % 10;
}
n = (int) Math.pow(10, n-1);
if (n > num){
return 0;
}
num /= n;
return num % 10;
}
public int getMaxNumDigits(int[] nums){
int max = nums[0];
for(int i=0; i<nums.length; i++){
max = max > nums[i] ? max : nums[i];
}
String sax = String.valueOf(max);
return sax.length();
}
10.3 时间复杂度
平均时间复杂度:O(n*k)
最差时间复杂度:O(n*k)