[数据结构与算法]LeetCode 74 搜索二维矩阵

https://leetcode-cn.com/problems/search-a-2d-matrix/https://leetcode-cn.com/problems/search-a-2d-matrix/https://leetcode-cn.com/problems/search-a-2d-matrix/

编写一个高效的算法来判断?m x n?矩阵中，是否存在一个目标值。该矩阵具有如下特性：

每行中的整数从左到右按升序排列。
每行的第一个整数大于前一行的最后一个整数。
?

示例 1：

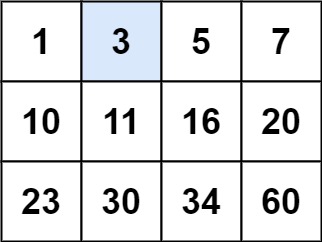
输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
输出：true
示例 2：

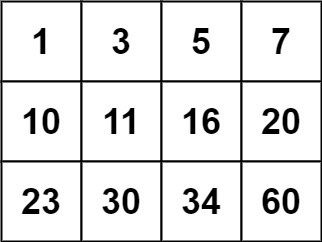
输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13
输出：false

这是一道二分的标准练习题，那么废话不多说直接上代码。

class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
       int upp=0,downp=matrix.size()-1,midd;
       while(upp<=downp){
           midd=upp+(downp-upp)/2;
           if(matrix[midd][0]==target){
               return true;
           }
           else if(matrix[midd][0]>target){
               downp=midd-1;
           }
           else{
               if(matrix[midd][matrix[midd].size()-1]>target){//找到了行
                    //那就再对这个行使用炎拳（划掉），二分吧
                    int leftp=0,rightp=matrix[midd].size()-1,midp;
                    while(leftp<=rightp){
                        midp=leftp+(rightp-leftp)/2;
                        if(matrix[midd][midp]==target){
                            return true;
                        }
                        else if(matrix[midd][midp]>target){
                            rightp=midp-1;
                        }
                        else{
                            leftp=midp+1;
                        }
                    }
                    return false;
               }
               else if(matrix[midd][matrix[midd].size()-1]==target){
                   return true;
               }
               else{
                   upp=midd+1;
               }
           }
       }
       return false;
    }
};

简单讲解一下我的思路，首先我们看图得知是从上到下，从左到右不断增大的矩阵，那么就先找到符合我们要求的那一行，我们不断把每行的首数字和Target进行比较。（使用二分法）

稍微记录一下二分法中的小知识点：

mid值的计算式优先使用leftpoint+(rightpoint-leftpoint)/2而不是(leftpoint+rightpoint)/2,因为前者数值溢出的可能性更小，至于两者等价的原因可以用简单的数学式来推导记录

(leftpoint+rightpoint)/2=leftpoint/2+rightpoint/2=leftpoint-leftpoint/2+rightpoint/2

=leftpoint+(rightpoint-leftpoint)/2? 这样就比较易于记忆。

行首数字和Target比较的时候，如果大于Target，则不论后面的还是下面的都肯定大于Target，我们直接取将二分范围上调；如果是小于Target，我们在把Target和行末数字比较，来判断目标是在该行，还是在下面的范围。