[数据结构与算法]线段树模板

线段树是一个区间二叉树，用来处理区间和、区间最大值、区间最小值等区间问题。

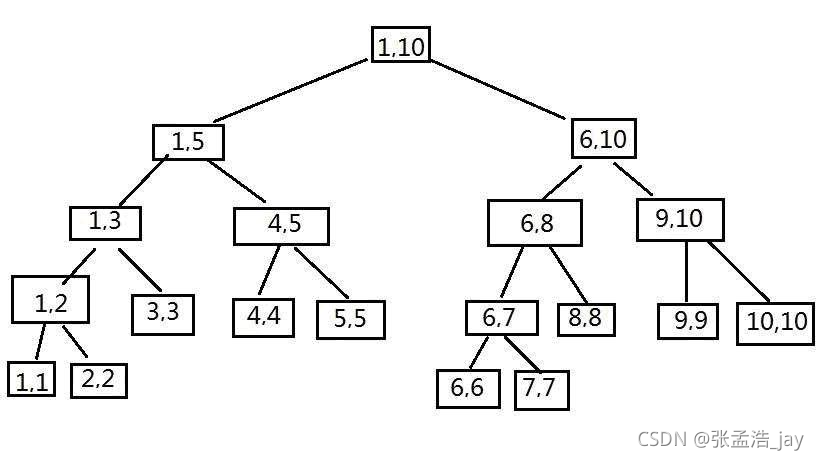
线段树的节点存储着对应的区间信息、以及维护的最大值或者是最小值信息。

线段树是一个完全二叉树，用一个数组来存储，根节点的下标为1，左子节点为2* i，右子节点为2*i+1。

对应的区间信息其实不用存储，都是在代码中维护的，因为每次都是将一个区间按照mid来分为[l,mid]和[mid+1,r]两个左右子区间。

线段树针对的是区间的动态更新和查找，修改和查找的时间复杂度都是log(n)。

因为普通的前缀和的查找时间虽然是O(1)，但是更改却是O(n)。

线段树中可以通过惰性更新来增加性能。当更新的时候只更新父节点，只有子节点在被更新或者访问的时候，才会将对应的父节点下推，也就是pushDown，将之前的更新下推到子节点。

下面是一个求区间最大值的线段树模板：

class SegmentTree{
    
    int n;
    int[] tree;
    int[] lazy;
    int[] arr;
    public SegmentTree(int n,int[] arr){
        tree = new int[4 * n];
        lazy = new int[4 * n];
        this.n = n;
        this.arr = arr;
    }
    
    //根据一个arr来初始化线段树
    public void build(int l,int r,int id){
        if(l == r){
            tree[id] = arr[l];
            return;
        }
        
        int mid = (l + r)/2;
        
        build(l,mid,id<<1);
        build(mid+1,r,(id<<1)+1);
        //根据子节点来更新父节点
        pushUp(id);
    }
    
     //根据子节点来更新父节点
    public void pushUp(int id){
        tree[id] = Math.max(tree[id<<1],tree[(id<<1) +1]);
    }
    
     //惰性更新，当要访问父节点的子节点的时候，需要将之前的更新下推给子节点
    public void pushDown(int id){
        tree[id<<1] = Math.max(tree[id<<1],lazy[id]);
        tree[(id<<1)+1] = Math.max(tree[(id<<1)+1],lazy[id]);
        
        lazy[id<<1] = Math.max(lazy[id<<1],lazy[id]);
        lazy[id<<1|1] = Math.max(lazy[(id<<1)+1],lazy[id]);
        
        lazy[id] = 0;
    }
    
    //区间更新
    public void update(int l,int r,int x,int y,int val,int id){
        
        if(x <= l && r <= y){
            tree[id] = Math.max(tree[id],val);
            lazy[id] = Math.max(lazy[id],val);
            return;
        }
        
        int mid = (l + r)/2;
        pushDown(id);
        if(x <= mid){
            update(l,mid,x,y,val,id<<1);
        }
        
        if(y >= mid + 1){
            update(mid+1,r,x,y,val,(id<<1)+1);
        }
        
        pushUp(id);
    }
    
    //区间查询
    public int query(int l,int r,int x,int y,int id){
        if(x <= l && r <= y){
            return tree[id];
        }
        
        int mid = (l + r) / 2;
        int ans = 0;
        pushDown(id);
        if(x <= mid){
            ans = Math.max(ans,query(l,mid,x,y,id<<1));
        }
        
        if(y >= mid + 1){
            ans = Math.max(ans,query(mid+1,r,x,y,(id<<1)+1));
        }
        
        return ans;
    }
}