来简单记录一下二叉树的前中序遍历。
分为前中序遍历和后序遍历来拆开记录。
?
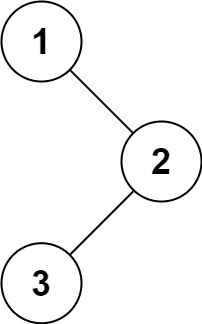
输入:root = [1,null,2,3] 输出:[1,2,3]
前序中序的代码大相径庭,只是记录输出的时间点不一样。
首先都需要一个记录输出答案的ans动态数组,一个结点指针类型的栈和一个结点指针。
vector<int> ans;//首先建立一个ans动态数组记录答案
stack<TreeNode*> s;
TreeNode* cur=root;然后开始循环:
while(!s.empty()||cur!=nullptr){
while(cur!=nullptr){
ans.push_back(cur->val);//压入答案
s.push(cur);
cur=cur->left;
}
cur=s.top();//栈顶元素是不断向左结点移动最后找到的左结点为空的结点
cur=cur->right;
s.pop();
}思路是当栈为空且当且结点也为空的时候结束循环。
当当前结点不为空的时候就一直往左结点走,一直把结点入栈(此时如果是前序遍历的话则一边把结点入栈一边把值压入ans数组),一直走到没有左结点可走为止。以下图举例的话第一次跳出循环的时候栈顶元素应该是蓝色的位置。

然后我们已知左结点为空(如果是中序遍历,这时才是将值压入ans数组的时机),我们就向右移动,并弹出栈顶元素,因为已经向右移动了而且不论前序还是中序遍历此时这个结点的值都已经被记录过了。
最后附上完整的前中序遍历迭代代码
class Solution {//前序遍历
public:
vector<int> preorderTraversal(TreeNode* root) {
vector<int> ans;//首先建立一个ans动态数组记录答案
if(root==nullptr){
return ans;
}
stack<TreeNode*> s;
TreeNode* cur=root;
while(!s.empty()||cur!=nullptr){
while(cur!=nullptr){
ans.push_back(cur->val);//压入答案
s.push(cur);
cur=cur->left;
}
cur=s.top();//栈顶元素是不断向左结点移动最后找到的左结点为空的结点
cur=cur->right;
s.pop();
}
return ans;
}
};class Solution {//中序遍历
public:
vector<int> inorderTraversal(TreeNode* root) {
vector<int> ans;
stack<TreeNode*> s;
TreeNode* cur=root;
while(!s.empty()||cur!=nullptr){
while(cur!=nullptr){
s.push(cur);
cur=cur->left;
}
cur=s.top();
ans.push_back(cur->val);
s.pop();
cur=cur->right;
}
return ans;
}
};后序遍历的话之后再写,现在摸了?