[数据结构与算法]数据结构-栈与队列--队列

概念

• 队列是一种有序表，它的插入操作（添加和压入）和删除操作（移除或出栈）分别在列表的两端，插入新元素的一端称为队尾，删除元素的那一端被称为队首。
  

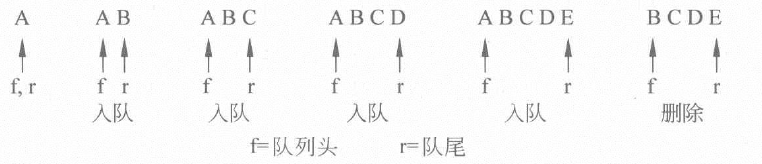
普通队列

• 上面也提到了，删除元素从队首删除，插入元素从队尾插入，若是普通的单队列，当队尾指针到达最大容量时，我们该怎么利用队首删除掉元素的存储空间，如下图：
  
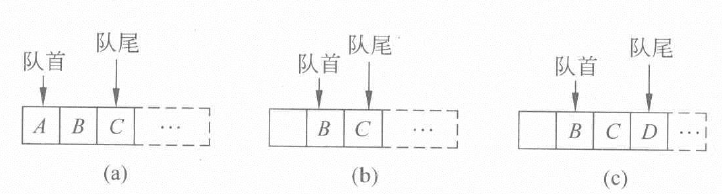
• 一种方法时将所有元素左移到队首，如下图：
  
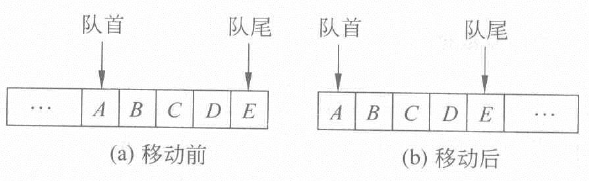
  不过这种方法的时间复杂度正比于队列长度，比较花费时间；
• 下面将介绍一种方法在时间复杂度为$O(1)$的情况下解决该问题

循环队列

• 循环队列示意图如下：
  
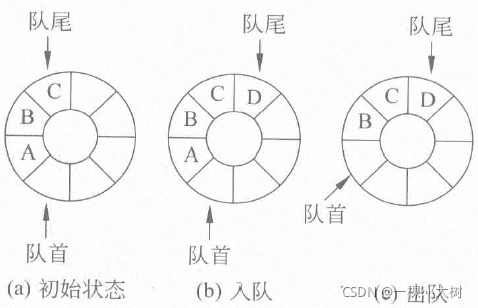
• 这里队首$(front)$指向队首元素沿逆时针方向的下一个位置，队尾$(rear)$定义不变，当添加元素时，$rear$的改变关系为：
  if(rear==capacity-1)rear=0; else rear++;
• 其实该关系式等价于
  rear=(rear+1)%capacity;

定义ADT

• 这里定义的为循环队列

template<class T>
class Queue
{
public:
	//构造空队列
	Queue(int queuecapcity = 10);
	//队列是否为空
	bool isEmpty()const;
	//返回头元素
	T& Front()const;
	//返回尾元素
	T& Rear()const;
	//队列扩大两倍
	void DoubleSize();
	//向队列中添加新元素
	void Push(const T& item);
	//删除头元素
	void Pop();
private:
	T* queue;
	int front;   //在队首逆时针的下一个位置
	int rear;    //队尾所在位置
	int capcity; //队列容量
};

容量扩展

• 在添加元素前，我们要判断队列是否已满，我们要进行容量扩展，因为我们定义的为循环队列，所以当$rear==front$时，就可以确定队列容量已满，此时我们要新建一个容量为两倍的队列，将原队列的元素从队首开始到队尾复制到新队列的最左边原队列指向新队列的地址，如下图：

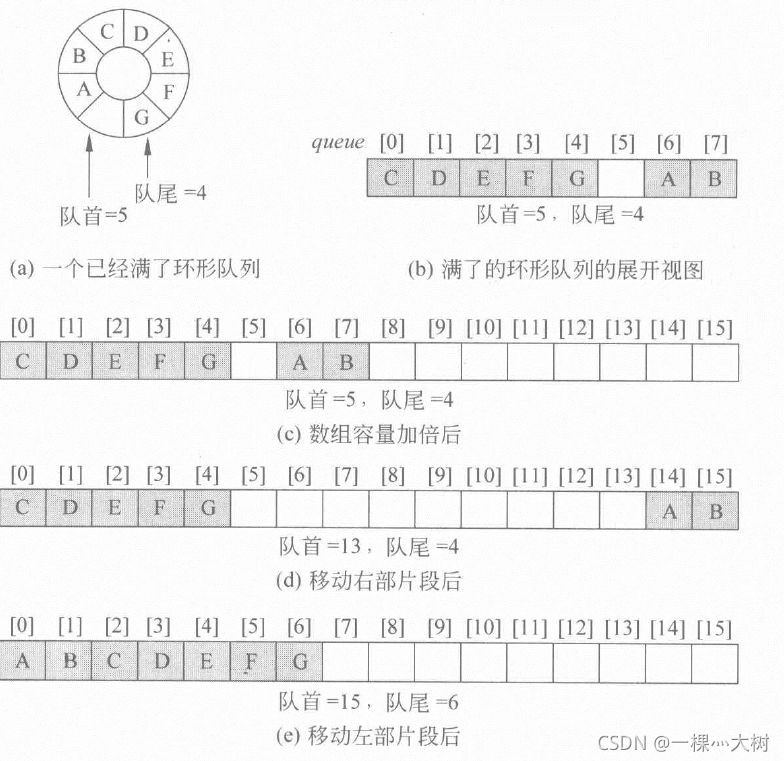
具体函数如下：

template<class T>
void Queue<T>::DoubleSize()
{
	T* newqueue = new T[2 * capcity];
	int start = (front + 1) % capcity;
	if (start < 2)
	{
		copy(queue + start, queue + start + capcity - 1, newqueue);
	}
	else
	{
		copy(queue + start, queue + capcity, newqueue);
		copy(queue, queue + rear + 1, newqueue + capcity - start);
	}

	front = 2 * capcity - 1;
	rear = capcity - 2;
	capcity *= 2;
	delete[]queue;
	queue = newqueue;
}

添加元素

• 既然我们已经解决了容量扩展的问题，添加元素就很容易了，函数如下：

template<class T>
void Queue<T>::Push(const T& item)
{
	if ((rear + 1) % capcity == front)
	{
		DoubleSize();
	}
	rear = (rear + 1) % capcity;
	queue[rear] = item;
}

删除元素

• 类似于栈的删除（详情见：数据结构-栈与队列–栈）
• 函数如下：

template<class T>
void Queue<T>::Pop()
{
	if (isEmpty())throw"队列为空！无法删除！";
	front = (front + 1) % capcity;
	queue[front].~T();
}

代码总览

#include<iostream>
using namespace std;

template<class T>
class Queue
{
public:
	//构造空队列
	Queue(int queuecapcity = 10);
	//队列是否为空
	bool isEmpty()const;
	//返回头元素
	T& Front()const;
	//返回尾元素
	T& Rear()const;
	//队列扩大两倍
	void DoubleSize();
	//向队列中添加新元素
	void Push(const T& item);
	//删除头元素
	void Pop();
private:
	T* queue;
	int front;   //在队首逆时针的下一个位置
	int rear;    //队尾所在位置
	int capcity; //队列容量
};

template<class T>
Queue<T>::Queue(int queuecapcity)
{
	if (queuecapcity < 1)throw"队列容量必须大于0";
	capcity = queuecapcity;
	queue = new T[capcity];
	front = rear = 0;
}

template<class T>
bool Queue<T>::isEmpty() const
{
	return front==rear;
}

template<class T>
T& Queue<T>::Front() const
{
	if (isEmpty())throw"队列为空！";
	return queue[(front + 1) % capcity];
}

template<class T>
T& Queue<T>::Rear() const
{
	if (isEmpty())throw"队列为空！";
	return queue[rear];
}

template<class T>
void Queue<T>::DoubleSize()
{
	T* newqueue = new T[2 * capcity];
	int start = (front + 1) % capcity;
	if (start < 2)
	{
		copy(queue + start, queue + start + capcity - 1, newqueue);
	}
	else
	{
		copy(queue + start, queue + capcity, newqueue);
		copy(queue, queue + rear + 1, newqueue + capcity - start);
	}

	front = 2 * capcity - 1;
	rear = capcity - 2;
	capcity *= 2;
	delete[]queue;
	queue = newqueue;
}

template<class T>
void Queue<T>::Push(const T& item)
{
	if ((rear + 1) % capcity == front)
	{
		DoubleSize();
	}
	rear = (rear + 1) % capcity;
	queue[rear] = item;
}

template<class T>
void Queue<T>::Pop()
{
	if (isEmpty())throw"队列为空！无法删除！";
	front = (front + 1) % capcity;
	queue[front].~T();
}

上一节：数据结构-栈与队列–栈