赛事总结
题目方面
- 本次比赛的整个出题,我都严格把关了,继ABA出题组之后,ABC出题组的首战
- 一个很明显的方面就是,题目变得更加美观好看了(字母数字以及下标全部使用了
l
a
t
e
x
latex
latex,代码块全部使用了
反引号这样的形式) - 题目风格更加靠近天梯风格了
- 题目质量也算高了,所有不合天梯风格的idea都被我给砍掉了
- 经过了三次验题,正确性有了保障
出题组
A B A & A B ABA\&AB ABA&AB出题组退役, A B C ABC ABC出题组上位
组长:贝
组员:勋、杰、弛、举
难度把控
- 我们通过美化题面,反复完善、修改题意,方便大家理解,以及给出提示,来不断降低难度,达到一个适当的难度
- 发现整场码量还是有的,于是给出了4h比赛时间
- L2-3给验题人验了一遍,三个验题人也不会。。。.于是就给出了提示:多源点多汇点转换为单源点单汇点
- L3-1给出了完全二叉树的提示,因为某位不愿意透露姓名的PTA顶级满分验题人自己都忘记了完全二叉树定义,不想到出肯定很多人混淆了完全二叉树和完美二叉树的定义
- L3-3原本是一道校选第一水平写70分钟才能做出5分的送命题,被我换成这道容易骗分的,且有可能有人能做出来的题目了
模拟程度
- 可以说是最接近正式赛的一次校选了,不管是题目风格、题目难度还是比赛模式
- 模式上,只允许查看自己提交记录(看不到别人提交是WA还是MLE),但是可以看排名和其他选手的具体分数(正式赛有榜单可以看,可以参考队友的答题情况来答题)
L1 基础级
L1-1 最菜的
出题人:贝
算法思路
- 延续了JMU历年校选第一题的猜字谜风格,往年这种送分题,往年题面是全英文且还有转义源码,这次给的还是中文的
- 分为两种人,知道最菜的人是我的,10秒内就过了
- 如果不知道的话,按照最后的Hint提示,按照Hint说的步骤来,写个代码也过了
- 我一直在控制整个出题组的出题难度和方向,希望大家还是能多拿点分,区分度会更加明显一点。
代码实现
#include <bits/stdc++.h>
using namespace std;
int main()
{
string L="GNINIEBNIL";
for(int i = 0 ; i < L.size() ;i ++)
{
L[i]= L[i] - 'A' + 'a';
}
reverse(L.begin(),L.end()) ;
cout << L <<" shi JMU zui cai de ren.";
}
L1-2 复读机
出题人:贝
思路
- 妥妥送分题,没什么好说的
代码实现
#include <bits/stdc++.h>
using namespace std;
#define el '\n'
#define rep(i, a, b) for (int i = (a); i <= (b); i++)
int main()
{
cin.tie(0);
cout.tie(0);
rep(i, 1, 5)
cout << "beibei shi Jimei University zui cai de ren" << el;
}
L1-3 JMU仓颉再现——绝绝子的何式汉字
出题人:勋
题意
乱七八糟,最后一句是关键,即输出n行"—"
解题思路
输出n行"—"
验题人贝贝吐槽:这个既不是中文汉字“一”,也不是加减乘除的“-”,而是破折号的一半“—”
真是父亲给挖儿子坟——掘掘子
代码
#include<bits/stdc++.h>
using namespace std;
int main()
{
int n;
cin >> n;
for (int i = 0; i < n; i++)
{
if (i)cout << endl;
cout << "—";
}
}
L1-4 死脑筋
出题人:杰
算法思路
兑换后的瓶子,也可以重复兑换,循环结构模拟兑换过程即可,直至不能再兑换
代码实现
#include<bits/stdc++.h>
using namespace std;
int n, k, m;
int main()
{
cin >> n >> k;
int ans = 0;
do {
ans += n;
m += n; //得到n个瓶盖
n = m / k;
m %= k;
}while(n);
cout << ans;
}
L1-5 反·复读机
出题人:贝
出题报告
- 我怕有人被卡了行末空格等等一些七七八八的,我还在题干最后特意提醒了……
- 我设置了6个测试点
- 测试点0,基本正确,小数据,3分
- 测试点1,仅一句话,1分
- 测试点2,三句话相同,1分
- 测试点3,两句话,1分
- 测试点4,大数据 n = 1 e 5 n=1e5 n=1e5,发言长度均为100个字符,8分
- 测试点5,大数据 n = 1 e 5 n=1e5 n=1e5,所有发言均相同的情况,1分
算法思路
- 我们直到遇到不同的发言的时候,再输出前一句发言
- 然后我们开一个
cnt来统计一下前一句发言出现了几次,再考虑他是否需要去重 - 但是这样我们最后必然还会剩下一次,所以最后在输出一次即可
代码实现
#pragma GCC optimize("O3")
#include <bits/stdc++.h>
#include <unordered_map>
#include <unordered_set>
using namespace std;
#define debug(x) cerr << #x << ": " << x << '\n'
#define bd cerr << "----------------------" << el
#define el '\n'
#define cl putchar('\n')
#define pb push_back
#define eb emplace_back
#define x first
#define y second
#define rep(i, a, b) for (int i = (a); i <= (b); i++)
#define loop(i, a, b) for (int i = (a); i < (b); i++)
#define dwn(i, a, b) for (int i = (a); i >= (b); i--)
#define ceil(a, b) (a + (b - 1)) / b
#define ms(a, x) memset(a, x, sizeof(a))
#define inf 0x3f3f3f3f
#define db double
typedef long long LL;
typedef long double LD;
typedef pair<int, int> PII;
typedef pair<db, db> PDD;
typedef vector<int> vci;
typedef map<int, int> mii;
typedef mii::iterator mii_it;
const int N = 1e5 + 10, M = 2e6 + 10, E = 1e3 + 10, md = 1e9 + 7;
const double PI = acos(-1), eps = 1e-8;
int T, n, m, cnt;
string last, now;
void out()
{
if (cnt < 3)
{
rep(i, 1, cnt)
{
cout << last << el;
}
}
else
cout << last << el;
return ;
}
int main()
{
// freopen("2.in", "r", stdin);
// freopen("2.out", "w", stdout);
cin.tie(0);
cout.tie(0);
cin >> n;
getchar();
rep(i, 1, n)
{
getline(cin, now);
if (now != last)
{
if(cnt)
out();
cnt = 1;
last = now;
}
else
{
cnt++;
}
}
out();
}
L1-6 不同的字符串
出题人:弛
题目陈述
大意:每组测试数据,给出n个字符串,问总共有几个不一样的字符串,不区分大小写
解题思路
-
先整行读入字符串,因为字符串中有空格,不能直接
cin和scanf,推荐getline(cin,s)读入整行 -
遍历整个字符串把小写字母变成大写统一字母大小写。不要去掉空格,因为aa aa和aa aa是两个不相同的字符串。
-
第一种办法使用set,直接把字符串存入set中,最后输出set中的个数就可以(set有自动去重的功能)。
如果不会使用set的话,可以建一个字符串数组,把每一个新输入的字符串和数组中的每一个逐位进行比较,都不一样的话,将新字符串放入数组,然后不同的字符串个数加1。
代码实现
//方法一:使用set
#include<bits/stdc++.h>
using namespace std;
#define ll long long
typedef pair<int, int> PLL;
#define inf 0x3f3f3f3f
int main(){
int t;
cin>>t;
while(t--){
int n;
cin>>n;
getchar();
set<string>s;
for(int i=0;i<n;i++){
string a;
getline(cin,a);
int len=a.length();
for(int j=0;j<len;j++){
if(a[j]>='a'&&a[j]<='z')a[j]=a[j]-'a'+'A';
}
s.insert(a);
}
cout<<s.size()<<endl;
}
}
//方法2:
#include<bits/stdc++.h>
using namespace std;
#define ll long long
typedef pair<int, int> PLL;
#define inf 0x3f3f3f3f
string a[1100];
int tot = 0;
int main() {
int t;
cin >> t;
while (t--) {
int n;
cin >> n;
getchar();
int cnt = 0;
for (int k = 0; k < n; k++) {
string s;
getline(cin, s);
int len = s.length();
for (int j = 0; j < len; j++) {
if (s[j] >= 'a' && s[j] <= 'z')s[j] = s[j] - 'a' + 'A';
}
int i;
for (i = 0; i < cnt; i++) {
int len2 = a[i].length();
if (len2 != len)continue;
int j;
for (j = 0; j < len; j++) {
if (a[i][j] != s[j])break;
}
if (j == len)break;
}
if (i == cnt)a[cnt++] = s;
}
cout << cnt << endl;
}
}
L1-7 FJCC-GPLT
出题人:勋
题目陈述
给定n个队伍的10个人得分,按照天梯赛的规则模拟,计算每个队伍的得分并进行排序。
解题思路
- 按照行输入进行队伍名字的读取
- 对于每个队伍,进行10个人15道题的得分输入,处理出这个队伍的l1,l2,l3分别有多少分
- 判断l1分数是否够800分,足够的情况下总分加上l2的分数,在l1分数够800分l2的分数够400分的情况下总分加上l3的分数,注意判断l3的分数是否有效的同时要先满足l2的分数有效,防止l2的分数够400分但是其分数是无效的。
- 最后按照队伍分数为第一关键字,队伍名字字典序对第二关键字进行排序然后输出即可。
代码实现
#include<bits/stdc++.h>
#include<bits/stdc++.h>
using namespace std;
map<string, int> m;
vector<pair<int, string>> p;
int main()
{
int n;
cin >> n;
getchar();
for (int i = 0; i < n; i++)
{
string s;
getline(cin, s);
int l1 = 0, l2 = 0, l3 = 0;
for (int l = 0; l < 10; l++)
{
int g;
for (int j = 0; j < 15; j++)
{
cin >> g;
if (j < 8)l1 += g;
else if (j < 12)l2 += g;
else l3 += g;
}
}
int res = l1;
if (l1 >= 800)res += l2;
if (l1>=800&&l2 >= 400)res += l3;
getchar();
p.push_back(make_pair(-res, s));
}
sort(p.begin(), p.end());
for (auto k : p)
{
cout << k.second << ' ' << -k.first << endl;
}
}
L1-8 『谁在说谎』
出题人:贝
出题报告
-
原本我还想卡掉double的精度,直接比较总和long long,精度肯定比直接比较平均值来的高,后面思索了一下,还是没刻意去卡
-
这题我设置了4个测试点
-
不会真有人用“lbn”、“LBN”来表示 a 0 a_0 a0?对应的字符串?
-
测试点1,基本正确,4分
-
测试点2,最大数据,全部正确,得开long long ,10分
-
测试点3,基本正确,但是会被“lbn”,“LBN”卡掉,5分
-
测试点4,测试nobody,1分
-
因为 1 0 5 × 1 0 5 = 1 0 10 10^5 \times 10^5 =10^{10} 105×105=1010,所以需要开LL
算法思路
- 用map很简单,两个map记录值就行了,map自带排序,记得开LL,秒过
- 自己手写哈希的话也还好,一个字符串最多长度就5位,把他看成26进制即可
代码实现
#pragma GCC optimize("O3")
#include <bits/stdc++.h>
#include <unordered_map>
#include <unordered_set>
using namespace std;
#define debug(x) cerr << #x << ": " << x << '\n'
#define bd cerr << "----------------------" << el
#define el '\n'
#define cl putchar('\n')
#define pb push_back
#define eb emplace_back
#define x first
#define y second
#define rep(i, a, b) for (int i = (a); i <= (b); i++)
#define loop(i, a, b) for (int i = (a); i < (b); i++)
#define dwn(i, a, b) for (int i = (a); i >= (b); i--)
#define ceil(a, b) (a + (b - 1)) / b
#define ms(a, x) memset(a, x, sizeof(a))
#define inf 0x3f3f3f3f
#define db double
typedef long long LL;
typedef long double LD;
typedef pair<int, int> PII;
typedef pair<db, db> PDD;
typedef vector<int> vci;
typedef map<int, int> mii;
typedef mii::iterator mii_it;
const int N = 110, M = 2e6 + 10, E = 1e3 + 10, md = 1e9 + 7;
const double PI = acos(-1), eps = 1e-8;
int T, n, m;
map<string , LL> last, now;
string name[N];
string b = "1", s;//因为S是由字母组成的,故用数字字符串来代表贝贝可以避免哈希冲突
//考察哈希中的状态设计
LL x;
int main()
{
// freopen("2.in", "r", stdin);
// freopen("2.out", "w", stdout);
cin.tie(0);
cout.tie(0);
cin >> n >> m;
rep(i, 1, m)
{
cin >> x;
last[b] += x;
}
rep(i, 1, n)
{
cin >> s;
name[i] = s;
rep(i, 1, m)
{
cin >> x;
last[s] += x;
}
debug(last[s]);
}
cin >> now[b];
int cnt = 0;
rep(i, 1, n)
cin >> now[name[i]];
for (auto it : last)
{
if(it.y >= last[b] && now[it.x] < now[b])
{//历史平均值比贝贝高,且报出成绩比贝贝低
cnt ++ ;
cout << it.x << el;
}
}
if(!cnt)
{
cout << "Yeah! Nobody!" <<el;
}
}
L2 进阶级
L2-1树的高度
出题人:举
题意
建树,求树的高度(树的层数)
解题思路
根据题意建好树之后,dfs一下就行。
代码
#include<bits/stdc++.h>
using namespace std;
const int maxn = 1e5 + 10;
vector<int> G[maxn];
int ans = 0;
// 根节点深度为1
void dfs(int cur, int deep) {
ans = max(ans, deep);
for (auto& val : G[cur]) {
dfs(val, deep + 1);
}
}
// i从0开始 a[i] 表示i+1的父亲编号
int main() {
ios::sync_with_stdio(false);
int n;
cin >> n;
int i;
int num;
for (i = 1; i < n; i++) {
cin >> num;
G[num].push_back(i);
}
dfs(0, 1);
cout << ans << endl;
return 0;
}
L2-2 ACM膜文化
出题人:贝
出题报告
考察set、string的应用,我设置了7个测试点
- 测试点0. 具备别名情况,基本正确,5分
- 测试点1. 区分大小写的别名,小数据,1分
- 测试点2. 区分大小写的别名,小数据,1分
- 测试点3. 不具备别名情况,基本正确,4分
- 测试点4. n最大,行长度字符最长,具备别名大小写,9分
- 测试点5.
Shen根据题意应该被判断为Normal,卡Shen的情况,以及Shen和shen的大小写都出现的情况。膜拜行为中这个人没有出现,但是判断为Dalao,只记录出现过的会被卡,3分 - 测试点6. 比如
JieShen后续记录为Jie,会被卡掉,2分
算法思路
- 其实四个字符串分级是个幌子,只需要数字表示等级即可
- 遇到这种模拟题,只要是仔细思索一下,就可以省去很多弯路,如果直接打很容易bug越打越多
- 其实这题难度也不大,原本,我打算出的题目里,还包含每个人有多个别名,水平等级根据别名会发生改变
- 考虑了下整份的难度,我怕出太难了,就降低成最后呈现的版本了
- 四个
set<string>维护别名池,代表等级,跟他原来的名字其实没有多大关系 - 先用
string的find函数来找到空格,substr将这句话划分主谓表,然后string的find和substr函数来找关键词,就可以AC
代码实现
#pragma GCC optimize("O3")
#include <bits/stdc++.h>
#include <unordered_map>
#include <unordered_set>
using namespace std;
#define debug(x) cerr << #x << ": " << x << '\n'
#define bd cerr << "----------------------" << el
#define el '\n'
#define cl putchar('\n')
#define pb push_back
#define eb emplace_back
#define x first
#define y second
#define rep(i, a, b) for (int i = (a); i <= (b); i++)
#define loop(i, a, b) for (int i = (a); i < (b); i++)
#define dwn(i, a, b) for (int i = (a); i >= (b); i--)
#define ceil(a, b) (a + (b - 1)) / b
#define ms(a, x) memset(a, x, sizeof(a))
#define inf 0x3f3f3f3f
#define db double
typedef long long LL;
typedef long double LD;
typedef pair<int, int> PII;
typedef pair<db, db> PDD;
typedef vector<int> vci;
typedef map<int, int> mii;
typedef mii::iterator mii_it;
const int N = 1e5 + 10, M = 2e6 + 10, E = 1e3 + 10, md = 1e9 + 7;
const double PI = acos(-1), eps = 1e-8;
int T, n, m;
string name, line, sub, ver, pred;
int level1, level2, first_blank, second_blank;
char c;
set<string> L[5];
int get_level(string &s)
{
if (s == "ZhanShen")
return 4;
else if (s == "BeiShen")
return 1;
else if (s.size() > 4 && s.substr(s.size() - 4, 4) == "Shen")
return 3;
else
{
for(int i = 1; i <= 4; i ++ )
{
if(L[i].find(s) != L[i].end())//去别名池里面找
{
return i;
}
}
return 2;
}
}
int main()
{
cin.tie(0);
cout.tie(0);
cin >> n;
getchar();
while (n--)
{
cin >> name >> c;
getchar();
getline(cin, line);
cout << name << " : " << line << el;
first_blank = line.find(' ');
sub = line.substr(0, first_blank);//主语
second_blank = line.find(' ', first_blank + 1);
ver = line.substr(first_blank + 1, second_blank - first_blank - 1);//谓语
pred = line.substr(second_blank + 1, line.size() - 1 - second_blank);//表语
cout <<"Translate : ";
if (pred.find("low-level") != pred.npos ||
pred.find("stupid") != pred.npos || pred.find("fool") != pred.npos
|| pred.find("caigou") != pred.npos)
{
level1 = get_level(name);
cout << name;
switch(level1)
{
case 1:{
cout << " is ZiCao-ing now." << el;
break;
}
case 2:{
cout << " is MaiRuo-ing now." << el;
break;
}
case 3:
case 4:{
cout << " is ZhuangCai-ing now." << el;
break;
}
}
if(sub != name && sub != "I")
L[level1].insert(sub);
}
else if (pred.find("high-level") != pred.npos ||
pred.find("clever") != pred.npos || pred.find("genuis") != pred.npos
|| pred.find("talent") != pred.npos)
{
level1 = get_level(name);
level2 = get_level(sub);
cout << name;
if (level1 < level2)
{
cout << " is truly worshipping now." << el;
}
else {
cout << " worships for taking care of other people's feelings." <<el;
}
}
else cout <<"sto "<< name << " orz." <<el;
}
}
L2-3 菜到家了
出题人:贝
出题报告
概述
- 本题为一个多源点多汇点最短路问题,本质还是考察单源点单汇点最短路问题
- 该题考察的还是最短路径,只需要在模板上面加两个点即可—超级源点+超级汇点,就可以AC、
- 我也总共分为大致三档分数:
- 第一档:每次都直接选择生鲜超市或寄存点为起点,然后跑多遍最短路,预计得分 10 ? 16 分 10-16分 10?16分,两种最好情况分别为,过测试点1,2,5,6(p为起点,14分),或测试点1,2,3,4,6(q为起点,16分)
- 第二档:选择p,q中小的当起点,预计 18 ? 19 18-19 18?19分,过前5个测试点
- 第三档,正解超级源点+超级汇点,预计得分25分,过全部测试点。
数据分析
- 我设置了7个测试点
- 测试点1: n = 100 , m = 200 , p = q = 10 n=100,m=200,p=q=10 n=100,m=200,p=q=10,测试基本正确性,3分
- 测试点2: n = 100 , m = 200 , p = q = 10 n=100,m=200,p=q=10 n=100,m=200,p=q=10,测试基本正确性,3分,这两个测试点可以跑多次单源最短路径必过
- 测试点3: n = 1 e 5 , m = 2 e 5 , p = 5 e 4 , q = 10 n=1e5,m=2e5,p=5e4,q=10 n=1e5,m=2e5,p=5e4,q=10,3分
- 测试点4: n = 1 e 5 , m = 2 e 5 , p = 99990 , q = 10 n=1e5,m=2e5,p=99990,q=10 n=1e5,m=2e5,p=99990,q=10,测试只有生鲜超市和寄存点的情况,1分
- 测试点5: n = 1 e 5 , m = 2 e 5 , p = 10 , q = 5 e 4 n=1e5,m=2e5,p=10,q=5e4 n=1e5,m=2e5,p=10,q=5e4,4分
- 测试点6:测试所有的生鲜超市和寄存点都不连通的情况,1分
- 测试点7: n = 1 e 5 , m = 2 e 5 , p = 80 , q = 80 , w i ∈ [ 5 e 3 , 1 e 4 ] n=1e5,m=2e5,p=80,q=80,w_i \in[5e3,1e4] n=1e5,m=2e5,p=80,q=80,wi?∈[5e3,1e4],10分
算法思路推进
算法一:暴力+最短路径
- 最短路径问题中,起点终点无疑可以调换
- 一个很显然很暴力的思路,将每一个生鲜超市为起点,跑一次最短路径
- 然后每次最短路径中,再选择到寄存处最短的,设置为当次的最短距离
- 这样总共跑 p p p次最短路径就可以得到答案
- 我这边代码写的是 S P F A SPFA SPFA,当然用 D i j k s t r a Dijkstra Dijkstra写也是一样的(毕竟都是超时
复杂度分析
- 时间复杂度,对于最短路径,SPFA最短路平均情况是 O ( k ∣ E ∣ ) O(k|E|) O(k∣E∣), k k k为常数,但是如果出题人故意卡你,可能可以达到 O ( ∣ V ∣ ∣ E ∣ ) O(|V||E|) O(∣V∣∣E∣)(这种情况很少)如果用Dijkstra堆优化复杂度稳定 O ( V log ? E ) O(V \log E) O(VlogE),ACM竞赛的话推荐Dijk堆优化。建图为 O ( ∣ E ∣ ) O(|E|) O(∣E∣),每次跑完SPFA都要再扫描一次终点,为 O ( q ) O(q) O(q),最短路共需要跑 p p p次,总得时间复杂度为 O ( p ( k ∣ E ∣ + q ) ) O(p(k|E|+q)) O(p(k∣E∣+q))
- 空间复杂度,定义了一个队列,
dis,vis数组,为 O ( V ) O(V) O(V)
算法二:超级源点汇点+最短路径
- 在上面的过程中我们会发现,我们的 S P F A SPFA SPFA过程中,会跑过很多重复的路径
- 反复做这些过程,不仅耗时间,而且耗费空间
- 所以我们有什么办法能省去这些过程呢?如何优化成了本题的重点
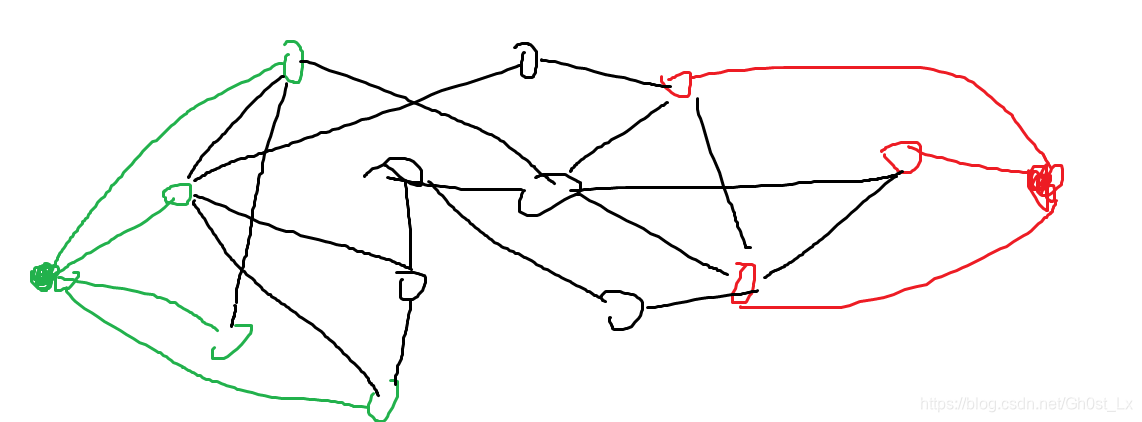
- 我们假设图为这样
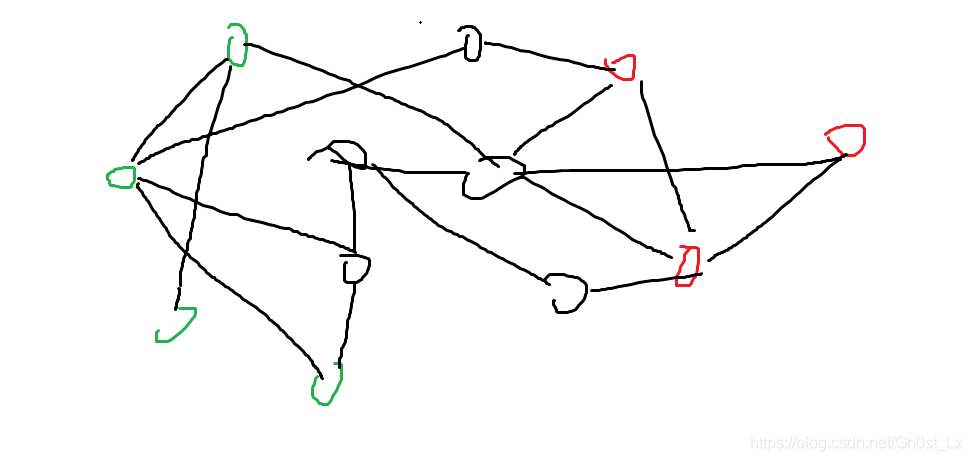
- 绿色代表生鲜超市,红色代表寄存处,黑色表示其他地点
- 此处我先说一个做法,然后再解释一下为什么这样做
- 假设生鲜超市都是同一个批发商,我们在生鲜超市与生鲜超市之间,我在它们之间安装一个“虫洞传送装置”不过分吧?
- 即绿色节点两两之间,都可以建立花费为0的连边,红色节点两两之间也可以
- 为什么可以这样做?
- 反证法,如果这是我们最后所求的最短路径的话,那么这条路径上除了起点和终点为,都只有黑色节点
- 如下图,假设我们求出来的答案是这样(1–>3),显然我们会发现一开始从2出发,会更优
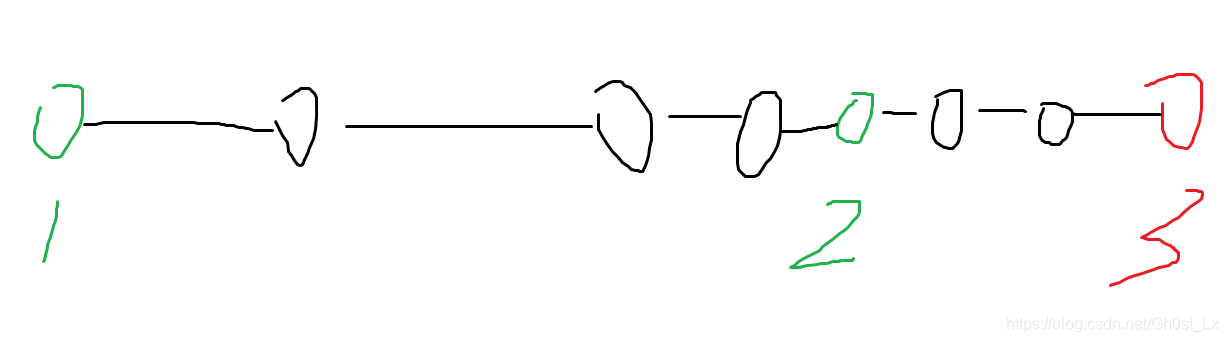
- 即,原来的路径上面如果存在非黑色节点,那么原来的最短路径一定能被更短的路径替代
- 这样建立新图之后,如果初始选择的源点跑出来的不是答案的最短路径,我们以及可以花费“0”(无条件转移到其他绿色节点),跑新的答案,这样就省略的重复求最短路径的过程
- 这样我们只需要同样的非黑色节点里面,两两建边(完全子图),最后只跑一次最短路径即可算出答案
再次优化
- 我们会发现只需要保证,同色的非黑色节点同色之间的联通性即可以,所以不需要建立完全子图,只需要建立成一棵树即可,这样建立边的时间有可以少很多
方案一
- P中的第一个节点到P其后的每一个节点都建立一个权值为0的边,即“菊花图”
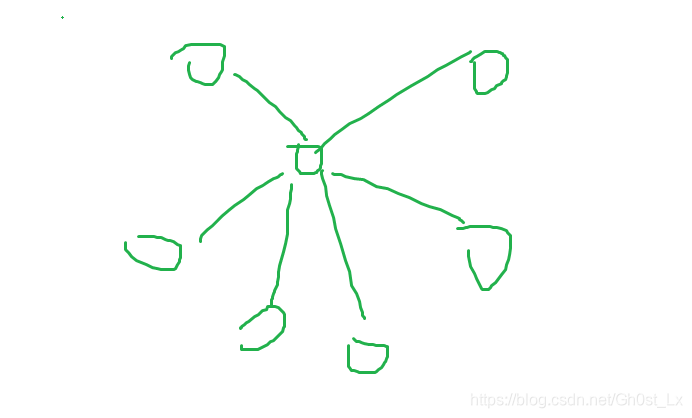
方案二
- P中下标前后相邻的两个建立权值为0的连边,即“链表“
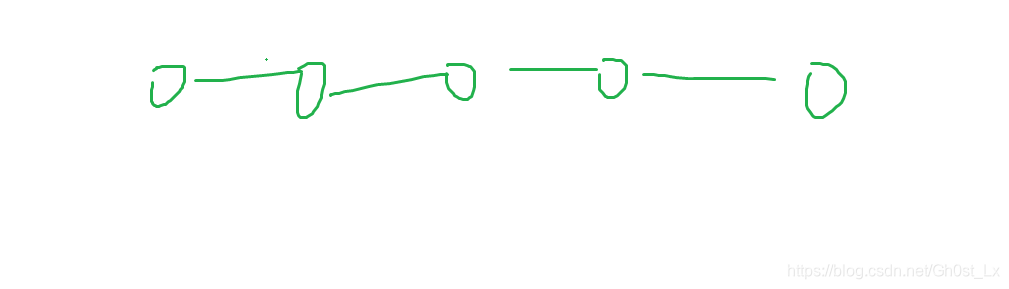
方案三
-
定义一个超级源点,编号为0,(图中没有用过),建立它和P中每个数权值为0的连边
-
此处我们选择方案三,上面两种也是可行的,但是方案三比较好写,代码量也比较小一点
-
(对于红色节点Q的实现方式同理)
复杂度分析
- 时间复杂度,对于最短路径,SPFA最短路平均情况是 O ( k ∣ E ∣ ) O(k|E|) O(k∣E∣), k k k为常数。建图为 O ( ∣ E ∣ ) O(|E|) O(∣E∣),建立超级源点汇点的连边为 O ( p + q ) O(p+q) O(p+q),总得时间复杂度为 O ( k ∣ E ∣ + p + q ) O(k|E|+p+q) O(k∣E∣+p+q)
- 空间复杂度,定义了一个队列,
dis,vis数组,为 O ( V ) O(V) O(V)
代码实现
#pragma GCC optimize("O3")
#include <bits/stdc++.h>
#include <unordered_map>
#include <unordered_set>
using namespace std;
#define debug(x) cerr << #x << ": " << x << '\n'
#define bd cerr << "----------------------" << el
#define el '\n'
#define cl putchar('\n')
#define pb push_back
#define eb emplace_back
#define x first
#define y second
#define rep(i, a, b) for (int i = (a); i <= (b); i++)
#define loop(i, a, b) for (int i = (a); i < (b); i++)
#define dwn(i, a, b) for (int i = (a); i >= (b); i--)
#define ceil(a, b) (a + (b - 1)) / b
#define ms(a, x) memset(a, x, sizeof(a))
#define inf 0x3f3f3f3f
#define db double
typedef long long LL;
typedef long double LD;
typedef pair<int, int> PII;
typedef pair<db, db> PDD;
typedef vector<int> vci;
typedef map<int, int> mii;
typedef mii::iterator mii_it;
const int N = 1e5 + 10, M = 2e6 + 10, E = 1e3 + 10, md = 1e9 + 7;
const double PI = acos(-1), eps = 1e-8;
int T, n, m, p, q;
int x, y;
vector<PII> v[N];
int SPFA()
{
queue<int> q;
q.push(0); //放入起点
bool vis[N]; //标记,是否在队列中
int dis[N]; //到起点的距离
memset(dis, 0x3f, sizeof dis); //初始化都是无穷大
memset(vis, 0, sizeof vis); //初始都不在队列中
vis[0] = 1; //起点已经入队
dis[0] = 0; //超级源点自己到自己的距离为0
while (!q.empty())
{
int u = q.front();
q.pop();
for (auto it : v[u])
{ //通过邻接表访问u的邻居
if (dis[u] + it.y < dis[it.x])
{ //如果可以对边进行松弛操作
dis[it.x] = dis[u] + it.y;
if (!vis[it.x])
{ //不在队列中 ,则将其放入队列中
vis[it.x] = 1;
q.push(it.x);
}
}
}
}
if (dis[n + 1] == dis[n + 2])
return -1; //如果图不连通
return dis[n + 1];
}
int main()
{
// freopen("6.in","r",stdin);
// freopen("6.out","w",stdout);
cin.tie(0);
cout.tie(0);
cin >> n >> m >> p >> q;
int u;
rep(i, 1, p)
{
cin >> u;
v[u].pb({0, 0});
v[0].pb({u, 0});
}
rep(i, 1, q)
{
cin >> u;
v[u].pb({n + 1, 0});
v[n + 1].pb({u, 0});
}
int a, b, c;
rep(i, 1, m)
{
cin >> a >> b >> c;
v[a].pb({b, c});
v[b].pb({a, c});
}
cout << SPFA() << el;
}
L2-4 你才菜到家了
题意
言简意赅,给一张无向图,求最小字典序的 M S T MST MST(最小生成树)
解题思路
- 思考经典求 M S T MST MST的贪心算法—— K r u s k a l Kruskal Kruskal,按边权值排序之后依次选择权值最小且不会构成环的边
- 权值不同的边只要先选小的才能保证生成树最小无需考虑边的名字,那么对于权值相同的若干条边,如果出现了"冲突"的情况即这些边只能选其中的部分几条,那么显然我们需要选边名字典序最小的那几条边
- 于是在排序边的时候按照边权为第一关键字, a . n a m e + b . n a m e < b . n a m e + a . n a m e a.name+b.name<b.name+a.name a.name+b.name<b.name+a.name为第二关键字排序,按照 k r u s k a l kruskal kruskal算法进行选边,最后判断是否存在生成树即可。
- 至于为什么每次选择边名字典序最小的边可以使得最后排序再拼接的字符串字典序最小,考虑经典的“拼接最小字典序的字符串”问题,因此按照 a . n a m e + b . n a m e < b . n a m e + a . n a m e a.name+b.name<b.name+a.name a.name+b.name<b.name+a.name为第二关键字排序即可。即可为题意中的组内边名字典序排序之后拼接的操作。故以此方法可以逐步构造一个字典序最小的 M S T MST MST
代码
#include<map>
#include<stdio.h>
#include<iostream>
#include<vector>
#include<string>
#include<math.h>
#include<queue>
#include<algorithm>
#include<cstring>
using namespace std;
#define ll long long
struct edge
{
string name;
int u, v, cost;
}e[200005];
int fa[100005];
int find(int r) { return fa[r] == r ? r : fa[r] = find(fa[r]); }
void join(int x, int y)
{
int fx = find(x), fy = find(y);
fa[fx] = fy;
}
bool cmp(edge a, edge b) { return a.cost < b.cost || (a.cost == b.cost && (a.name + b.name < b.name + a.name)); }
vector<string> ans;
int main()
{
int n, m;
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++)
{
fa[i] = i;
}
for (int i = 0; i < m; i++)
{
cin >> e[i].name;
scanf("%d%d%d", &e[i].cost, &e[i].u,&e[i].v);
}
sort(e, e + m, cmp);
for (int i = 0; i < m; i++)
{
int u = e[i].u, v = e[i].v;
if (find(u) != find(v))
{
ans.push_back(e[i].name);
join(u, v);
}
}
int c = 0;
sort(ans.begin(), ans.end());
for (int i = 1; i <= n; i++)
{
if (find(i) == i)c++;
}
if (c == 1)for (auto p : ans)cout << p;
else cout << "don't cout or printf me directly!!!!!!!\\Orz/";
}
L3 登顶级
L3-1 是否是合法的堆
出题人:贝
出题报告
概述
- 这题出题人觉得是绝世好题,极其浓的天梯风格,即结合了课内的数据结构,也有一定的难度
- 当时验题的时候,出题组五个人,除去这题的出题人我,还有另外三个人验题了,杰神40分钟就A了,勋总和弛神挣扎了好久最后也是A了。
- 一开始勋总给了个错误的毫无技术含量做法,然后也拿了20多分
- 我才想起来出这题数据那天我状态不好,随便搞了下除了这一题我没写出题分析外,其他的我出的题目出题分析我全写了,于是果断重新造了一份更强更全面的数据
- 毕竟现在是ABC出题组掌权,不能出现以前ABA出题组and AB出题组那样的错误(狗头保命)
- 所以后面我就又花了一整个晚上的时间,写了6份造数据的代码,造了一份极其全面的数据。
- 好的选拔赛,离不开优秀的题目和数据。
数据分析
-
这题我造了4个数据,每个数据都有 T = 10 T=10 T=10,这是为了防止纯
YES和NO可以骗分而设计的 -
测试点1,小数据 n ∈ [ 100 , 200 ] n \in [100,200] n∈[100,200],测试算法的基本正确性质,这题给的实现,就算是每个点都当根节点泡一遍也可以过,10分
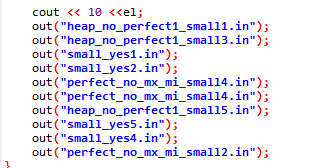
-
以上是我生成该测试点数据用的代码,由10个小数据组成,其中的
small代表这个是小数据点,其他根据英文含义自行领悟 -
测试点2,大数据,对于一部分 n ∈ [ 2 15 + 2 7 , 2 16 ? 2 7 ] n \in [2^{15}+2^7,2^{16}-2^7] n∈[215+27,216?27],另一部分 n ∈ [ 5 e 4 , 1 e 5 ] n \in [5e4,1e5] n∈[5e4,1e5],算法的大方向基本正确,9分
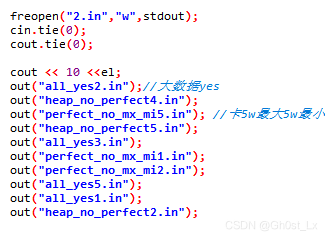
-
测试点3,大数据,对于一部分 n ∈ [ 2 15 + 2 7 , 2 16 ? 2 7 ] n \in [2^{15}+2^7,2^{16}-2^7] n∈[215+27,216?27],另一部分 n ∈ [ 5 e 4 , 1 e 5 ] n \in [5e4,1e5] n∈[5e4,1e5],其中一组包含一条链的情况,如果第一步直接递归搜索就会因为递归层数太深(10万层)而栈溢出,报RE(段错误),9分

-
我和勋总一同测试出上述的段错误,也是因为这个原本第二个测试点也包含链,于是我最后还是把第二个测试点中的链给删掉了
-
出题者认为,如果大方向没有错的话,也能拿21分,不至于被这个链卡掉,更具有区分度
-
测试点4,边界测试, n ≤ 2 n \leq 2 n≤2的情况,2分
-
心思缜密才能拿满
难度分析
- 验题人验题的时候发现难度确实是有的,我们出题组都做的这么吃力,更别说其他同学了
- 于是我根据了验题人做题的时间和反应,打算降低一下难度,提高得分率,于是我在hint里面给出了完全二叉树的解释,和关于题解的一点提示
- 因为发现出题组有4个人都做出了这题,但是是用了三种不同的方法,但是都用到了同一个东西,所以我就给出了最关键的提示。
- 多种解法也成为了这题的一个特色。
- 总体来看这题还是具有较大的难度。
- 为了提高得分率,我特地将600ms的时间限制,改为1500ms,怕有人会因cin或者scanf不够快而被卡掉,只要算法基本正确性在都可以过。
算法1:剪枝+堆的性质+map统计
出题人:贝
算法思路
- 第一眼看完题目,因为树是可以旋转的,第一反应一般都是全部找到所有最小值,再全部找到所有最大值,然后以其为根进行判断,后面发现可能有多个最大值和最小值,构造一组数据,有5k个最大值和5k个最小值,可以把这个错误的算法给卡掉,后面根据堆的性质,判断连边为2的节点,才可能是根,这样就优化了算法
- 接下来只需要以度为2的节点为根,判断他是否是一个合法的堆即可以,因为复杂度问题,判断是否是大小根堆的复杂度,明显小于判断是否是完美二叉树的,所以我们先判断是否是大小根堆
- 判断大小根堆很easy的,这边就不说了
- 判断是否是完美二叉树,可以构造出一组数据,如下
1
12
1 2 3 4 5 6 7 8 9 10 11 12
1 2
1 3
2 4
2 5
3 6
3 7
4 8
4 9
6 10
7 11
7 12
- 所以,如果只判断底层的话,再加上这棵树的左右节点可以互换,很明显是一种错误的思路,所以我们不止需要判断最底层,我们需要判断所有层数
- 首先先判断一下所有层的节点数是否合法,此处根节点为第0层,
num[i]代表第i层的节点数量,如果num[i]!=(1<<i)则不合法 num_leaf[i]代表以 i i i节点的子树中,所包含的叶子结点数量- 维护18个大顶堆(下标到17)( 2 16 ≤ 2^{16}\leq 216≤ n的最大值 ≤ 2 17 \leq 2^{17} ≤217)
- 令
x=1<<(d-i),nsum代表整棵树的叶子结点数,一层用一个堆表示,对于节点 i i i将num_leaf[i]放入第 h [ i ] h[i] h[i]个堆中,其中 h [ i ] h[i] h[i]代表第 i i i个节点在第几层 - 理论上同一层,应该只有若干个x值,和至多一个的非x值(即
nsum%x) - 可以理解为把叶子节点数量,作为一个标记数x ,如果它是一个合法的完美二叉树,对于每一层,最多仅由一个非x值
- 我们借助18个大顶堆或者18个map(因为同一层最多只有2种值),即可判断它是否是完美二叉树
- 至于如何判断,大顶堆的做法,如果
top()=x则直接pop,否则只有一种情况,就是top()=nsum%x并且heap.size()==1 - 这边
map里面储存两个值比这边快很多,也很好写,这边就不赘述了,同上一点。
代码实现
#include <bits/stdc++.h>
#include <unordered_map>
#include <unordered_set>
using namespace std;
#define el '\n'
#define eb push_back
typedef vector<int> vci;
const int N = 1e5 + 10;
int T, n, m, x, y, k, a[N], num[N], h[N], num_leaf[N], d;
vci v[N], rt, mx_id, mi_id;
//rt中储存的是边数大于2的,节点数
bool flag = 0, vis[N];
bool check_mi(int u, int fa)
{ //判断是否是小根堆
for (int i = 0; i < v[u].size(); i++)
{
int t = v[u][i];
if (t == fa)
continue;
if (a[t] < a[u])
return 0;
if (!check_mi(t, u))
return 0;
}
return 1;
}
bool check_mx(int u, int fa)
{ //判断是否是大根堆
for (int i = 0; i < v[u].size(); i++)
{
int t = v[u][i];
if (t == fa)
continue;
if (a[t] > a[u])
return 0;
if (!check_mx(t, u))
return 0;
}
return 1;
}
bool check_num()
{
for (int i = 1; i <= n; i++)
{
if (v[i].size() > 3)
return 0; //超过三条边,必然不是二叉树的根
if (v[i].size() == 2)
{
rt.eb(i);
}
}
if (rt.size() > 2)
return 0; //一个堆中sz==2的最多只有两个
return 1;
}
void get_leaf(int u)
{ //获取以当前节点为根的树中,第d层(最下面一层)的叶子结点数量
num_leaf[u] = 0; //多组样例,初值
if (h[u] == d)
{ //叶节点
num_leaf[u] = 1;
return;
}
for (int i = 0; i < v[u].size(); i++)
{
int t = v[u][i];
if (!vis[t])
{
vis[t] = 1;
get_leaf(t);
num_leaf[u] += num_leaf[t]; //加上他的子树中的num_l[]
}
}
}
bool check_per(int u)
{ //判断是否是完美二叉树
if (n <= 2)
return 1; //两个节点以下的,必然是
queue<int> q;
q.push(u);
memset(vis, 0, sizeof vis);
memset(h, 0, sizeof h);
memset(num, 0, sizeof num);
vis[u] = 1;
h[u] = 0;
num[0] = 1;
while (!q.empty())
{ //bfs搜索获取节点深度
int t = q.front();
q.pop();
for (int i = 0; i < v[t].size(); i++)
{
int w = v[t][i];
if (!vis[w])
{
vis[w] = 1;
q.push(w);
h[w] = h[t] + 1;
num[h[w]]++; //当前层数的节点数量
}
}
}
d = log(n) / log(2); //最大深度
for (int i = 1; i < d; i++)
{
if (num[i] != (1 << i))
return 0; //第i层具有(2^i)个节点
}
memset(vis, 0, sizeof vis);
vis[u] = 1;
get_leaf(u); //获取以当前节点为根的树中,第d层(最下面一层)的叶子结点数量
// priority_queue<int> heap[18]; //第i个大顶堆,储存深度为i的节点的num_l[]
map<int, int> mp[18];
for (int i = 1; i <= n; i++)
if (num_leaf[i])
mp[h[i]][num_leaf[i]] ++ ;
int nsum = n - (1 << d) + 1; //前d-1层有(1<<d)-1个节点,用n减去,即得到最后一层的节点数量,即num[d]…………i m sb
for (int i = d - 1; i >= 0; i--)
{
x = 1 << (d - i);
if(mp[i].size() > 2)
{
return 0;
}
else {
for(auto it : mp[i])
{
if(it.first !=x )
{
if(it.second > 1 || it.first != nsum % x)
return 0;
}
}
}
}
return 1;
}
void check()
{ //检查是否是一个合法的堆
for (int i = 0; i < rt.size(); i++)
if (check_mi(rt[i], 0) || check_mx(rt[i], 0)) //检查是否是小根堆,或者大根堆
if (check_per(rt[i]))
{ //检查是否是完美二叉树
flag = 1;
return;
}
}
void Pr(bool f)
{ //输出结果
if (f)
cout << "YES" << el;
else
cout << "NO" << el;
}
int main()
{
cin.tie(0), cout.tie(0), cin.sync_with_stdio(false);
cin >> T;
while (T--)
{
cin >> n;
rt.clear(); //初值
for (register int i = 1; i <= n; i++)
v[i].clear(); //初值
for (register int i = 1; i <= n; i++) //输入权值
cin >> a[i];
for (register int i = 1; i <= n - 1; i++)
{ //读入树形结构
cin >> x >> y;
v[x].eb(y), v[y].eb(x);
}
if (n <= 2)
{
Pr(1);
continue;
}
if (!check_num()) //检查节点的连边数量,是否合法
Pr(0);
else
{
flag = 0;
check();
Pr(flag);
}
}
}
算法2:剪枝+递归+大小根堆
验题人:勋
题意
给定一棵树,判断是否至少存在一种二叉树的组织形式使得其为一个大/小根堆。
解题思路
首先不难想到要从根节点入手,我们可以枚举根结点,但是直接枚举每个点明显时间复杂度过大(如果想不到如何优化,后续处理正确也是可以拿到不少分的),这里考虑作为一个堆的性质:是一个完全二叉树,具体完全二叉树的定义可以自行百度,这里不过多赘述。
所以来到本题的第一个难点——如何进行剪枝减少枚举情况:那么作为一个完全二叉树,其度不为3的结点最多为2个(即根结点和层序遍历的最后一个结点),反之则其不为一个完全二叉树。
同时根结点又必须是度为2的结点,也就是说,根结点的枚举次数最多为2,如果发现其不是完全二叉树,则可以直接输出错误。
因此,第一步我们进行计算每个结点的度并将度为2的结点记录下来,如果发现度为2的结点个数不在[1,2]范围内,则直接输出不满足即可(如果存在其他不满足二叉树的情况,例如:出现度>3或者度=0的结点也可以直接输出不满足,保证其为一棵二叉树方便后续处理)。
之后问题就变成了:给定根结点的情况下,如何判断一颗树为大/小根堆。
根据题目给出的大/小根堆的性质,我们可以将其拆分为两个问题:
- 是否一个完全二叉树
- 每个节点的权值应不小于(≥)或不大于(≤)其所有的子节点的值。
对于第2个问题就不多说了,给定了根结点简单进行两次(分别为大根堆、小根堆)递归判断即可。
那么来到本题第二个难点:如何判断一个树是否为完全二叉树。这个问题本身是并不困难的,但是关键在于本题的二叉树并没有明确限制左右子树,只给出了其两个儿子(或一个),左子树和右子树是可以进行交换的,只要存在任何一种子树的确定方式使得其为完全二叉树即可。
这里给出笔者的思路(欢迎加入自己的思考,查出错误共同学习):
递归判断每个结点两个孩子最多只能有一个是不完美二叉树,两个子树都是不完美二叉树则不可以,如果只有一个子树不完美则那个子树必须是比较高的子树
从根结点开始往下递归判断,不断维护每个结点的“不完美子树数k”(k∈{0,1,2}),对拥有不同个数子树的结点分类讨论(递归时需要记录父节点,形成父子结构,否则会往回走)
-
该结点没有子树,则k为0
-
该结点有且仅有一个子树,则k为1
-
该结点有两个子树,k为左右子树的k相加,若k=2则直接标记不是堆,否则判断左右子树的高度是否相同,若不同:
- 左子树高度>右子树高度,判断右子树的k是否为0(即右子树是否完美),如果不为0,则直接标记不是堆,如果为0,则将自己的k修改为1
- 右子树高度>左子树高度,判断左子树的k是否为0(即左子树是否完美),如果不为0,则直接标记不是堆,如果为0,则将自己的k修改为1
简而言之:
1.剪枝枚举根结点
2.判断是否为大/小根堆
3.判断是否为完美二叉树
代码
#include<bits/stdc++.h>
using namespace std;
#define ll long long
//谁出的题啊!写个题解写几k字!!!!!
//首先排除贝贝出的
typedef pair<int, int> PLL;
#define inf 0x3f3f3f3f
const int maxn = 100000 + 10;
int a[maxn];
int vis[maxn];
int wanmei[maxn];
vector<int>g[maxn];
vector<int>root;
bool check1(int u, int fa)
{
for (auto it : g[u])
{
if (it == fa) continue;
if (a[it] < a[u]) return false;
if (!check1(it, u)) return false;
}
return true;
}
bool check2(int u, int fa)
{
for (auto it : g[u])
{
if (it == fa) continue;
if (a[it] > a[u]) return false;
if (!check2(it, u)) return false;
}
return true;
}
bool ans = true;
int check_wanmei(int root, int& f) {//0没有 1一个 2多个
vector<int>x;
for (auto it : g[root]) {
if (!wanmei[it]) {
x.push_back(it);
wanmei[it] = 1;
}
}
if (x.size() == 2) {
int f1, f2;
int dep1, dep2;
dep1 = check_wanmei(x[0], f1);
dep2 = check_wanmei(x[1], f2);
f = f1 + f2;
if (f == 2)ans = false;
//if (abs(dep1 - dep2) > 2)ans = false;
if (dep1 == dep2);
else if (dep1 < dep2) {
if (f == 0)f = 1;
else if (!f1)ans = false;
}
else if (dep1 > dep2) {
if (f == 0)f = 1;
else if (!f2)ans = false;
}
return min(dep1, dep2) + 1;
}
else if (x.size() == 1) {
f = 1;
int ff;
return check_wanmei(x[0], ff);
}
else if (x.size() == 0) {
f = 0;
return 0;
}
return 0;
}
bool check_manzu(int root) {
memset(vis, 0, sizeof(vis));
queue<int>q;
vis[root] = 1;
q.push(root);
q.push(-1);
int flag = 0, flag2 = 0;
while (q.size()) {
int u = q.front();
q.pop();
if (u == -1) {
if (q.size() == 0)break;
if (flag || flag2)break;
q.push(-1);
continue;
}
int num = 0;
for (auto it : g[u]) {
if (!vis[it]) {
num++;
q.push(it);
vis[it] = 1;
}
}
if (num == 1) {
if (flag)return false;
else flag++;
}
else if (num == 0) {
flag2++;
}
}
if (flag > 1)return false;
while (q.size()) {
int u = q.front();
q.pop();
int num = 0;
for (auto it : g[u]) {
if (!vis[it]) {
num++;
q.push(it);
vis[it] = 1;
}
}
if (num != 0)return false;
}
return true;
}
bool check_wanquan(int root) {
memset(wanmei, 0, sizeof(wanmei));
ans = true;
int f;
wanmei[root] = 1;
if(check_manzu(root)){
check_wanmei(root, f);
return ans;
}
else {
return false;
}
}
bool check(int n)
{
if(n<=2)return true;
root.clear();
for (int i = 1; i <= n; i++)
{
if (g[i].size() > 3) return false;
if (g[i].size() == 2) root.push_back(i);
}
if (root.size() > 2) return false;
for (auto it : root) {
if (!check_wanquan(it))continue;
if (check1(it, 0) || check2(it, 0))return true;
}
return false;
}
int main() {
int t;
cin >> t;
while (t--) {
int n;
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> a[i];
g[i].clear();
}
for (int i = 1; i < n; i++) {
int u, v;
cin >> u >> v;
g[u].push_back(v);
g[v].push_back(u);
}
if (check(n))cout << "YES" << endl;
else cout << "NO" << endl;
//if (check_wanquan(1))cout << "YES" << endl;
//else cout << "NO" << endl;
}
}
算法3:高度差+递归
验题人:杰
算法思路
先确定根: 怎样的点可能会成为根:点权最小或最大的点,并且其度只能为 2 (因为堆是二叉堆)。如果这棵树是一个合法堆,那么度为 2 的点显然只能有两个。如果超过两个,则这棵树不可能是二叉堆。否则,令这些点作为根,尝试是否可以建成一棵合法堆。再特判一个 n<=2 时一定是合法堆
int solve() {
if(n<=2)return 1;
int num=0;
for(int i=1; i<=n; i++) {
if(vec[i].size()==2)num++;
if(vec[i].size()>3)return 0;
}
if(num>2)return 0;
for(int i=1; i<=n; i++) {
if(vec[i].size()==2&&a[i]==minval) {
flag=1;
dfs(i,0,0);//小根堆起跑
if(flag==1)return 1;
}
if(vec[i].size()==2&&a[i]==maxval) {
flag=1;
dfs(i,0,1);//大根堆起跑
if(flag==1)return 1;
}
}
return 0;
}
左右子树不能同时不满: 以下的满指的是满二叉树的意思。对于一个完全二叉树,考虑这个完全二叉树的根 u ,其需要满足:左子树满二叉树,右子树是完全二叉树,或者左子树是完全二叉树,右子树是满二叉树。且由于这道题每个点的左右子树可以任意交换,因此,只需要满足每个点的左右子树中至少有一棵是满二叉树即可。即:左右子树不能同时不满。
左右子树高度差不能大于1: 显然对于一棵完全二叉树,其左子树的高度最多比右子树的高度高1。
如何判断一棵树是个满二叉树? 左右子树均是满二叉树,且高度一致(这样就可以保证子树的满二叉树大小一致)。
代码实现
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+100;
vector<int>vec[N];
int a[N],tag,flag,high[N],siz[N],full[N],n,minval,maxval;
void dfs(int u,int fa,int key) {//key=0/1 表示在判断小根堆/大根堆
vector<int>son;
high[u]=siz[u]=1;
for(int i=0; i<vec[u].size(); i++) {
int v=vec[u][i];
if(v==fa)continue;
if(key==0) {
if(a[v]<a[u]) {
flag=0;
return;
}
} else {
if(a[v]>a[u]) {
flag=0;
return;
}
}
dfs(v,u,key);
siz[u]+=siz[v];
high[u]=max(high[u],high[v]+1);
son.push_back(v);
}
if(siz[u]==1)full[u]=1;//一个结点的完全二叉树
else {
if(full[son[0]]==1&&full[son[1]]==1&&high[son[0]]==high[son[1]])full[u]=1;//左右子树均满,且高度一致,则该树也是完全二叉树
else full[u]=0;
}
if(son.size()==0)return;
if(son.size()==1) {
if(high[son[0]]!=1)flag=0;
return;
}
if(son.size()==2) {
if(abs(high[son[0]]-high[son[1]])>1){
flag=0;
return;
}
if(full[son[0]]==0&&full[son[1]]==0) {
flag=0;
return;
}
}
}
int solve() {
if(n<=2)return 1;
int num=0;
for(int i=1; i<=n; i++) {
if(vec[i].size()==2)num++;
if(vec[i].size()>3)return 0;
}
if(num>2)return 0;
for(int i=1; i<=n; i++) {
if(vec[i].size()==2&&a[i]==minval) {
flag=1;
dfs(i,0,0);//小根堆起跑
if(flag==1)return 1;
}
if(vec[i].size()==2&&a[i]==maxval) {
flag=1;
dfs(i,0,1);//大根堆起跑
if(flag==1)return 1;
}
}
return 0;
}
int main() {
int T,u,v;
cin>>T;
while(T--) {
cin>>n;
minval=1e9;
maxval=-1e9;
for(int i=1; i<=n; i++) {
scanf("%d",&a[i]);
minval=min(minval,a[i]);
maxval=max(maxval,a[i]);
vec[i].clear();
full[i]=0;
}
for(int i=1; i<n; i++) {
scanf("%d%d",&u,&v);
vec[u].push_back(v);
vec[v].push_back(u);
}
if(solve())cout<<"YES"<<endl;
else cout<<"NO"<<endl;
}
return 0;
}
算法4:树的深度+递归+大小根堆
验题人:弛
算法思路
-
因为要求的是完全二叉树,所以连在根节点上的边只有两条(特判只有一个点,两个的情况,因为这个时候必然是一颗完全二叉树)。根据这个性质可以筛选出所有可能的根节点然后一个个判断过去。
-
先判断是否为完全二叉树再判断所有子节点大于还是小于父节点
-
完全二叉树的形式为除了最后一层是一颗满二叉树,然后最后一层所有节点都靠在左边,我们根据层次遍历去判断着课树是否满足除了最后一层是一颗满二叉树这个条件。
当找到某层中出现子节点只有一个或者没有的节点的时候,把当前层当成倒数第二层,对当前层和下一层进行节点判断即可。
因为没有规定左右节点,两边可以随意变换,所以上述的判断不能确定最后一层中的所有节点都可以放在最左边,也没有判断是不是只有一个 只有一个子节点的节点,还需要具体的判断一次(其实可以合并两次判断,一次性写完,但我总是写wa)
一个递归判断,记录左右子节点下属只有一个节点的个数,然后判断如果个数超过1是错误的,如果存在的子树深度浅也是错的(只有一个节点的子树肯定是延申到最后一层,所以深度最深)。
int check_wanmei(int root, int& f) { //0没有只有一个节点 1一个只有一个节点 2多个只有一个节点 返回的是深度 vector<int>x; for (auto it : g[root]) { if (!wanmei[it]) { x.push_back(it); wanmei[it] = 1; } } if (x.size() == 2) { int f1, f2; int dep1, dep2; dep1 = check_wanmei(x[0], f1); dep2 = check_wanmei(x[1], f2); f = f1 + f2; if (f == 2)ans = false;//存在了多个 只有一个子节点 if (dep1 == dep2);//深度一样的时候,只有一个子节点的子树左右可以互换没有要求 else if (dep1 < dep2) {//要求只有一个子节点的子树的深度较深 if (f == 0)f = 1; else if (!f1)ans = false; } else if (dep1 > dep2) { if (f == 0)f = 1; else if (!f2)ans = false; } return min(dep1, dep2) + 1; } else if (x.size() == 1) { f = 1; int ff; return check_wanmei(x[0], ff);//这个特殊的点不算深度 } //不用担心这个地方出现一直往下好几次的情况导致深度问题,上一个判断中已经保证了除了最后一层是一个满二叉树 else if (x.size() == 0) { f = 0; return 0; } return 0; } -
然后判断是否满足每个节点的权值应不小于(≥)或不大于(≤)其所有的子节点的值。
bool check1(int u, int fa) { for (auto it : g[u]) { if (it == fa) continue; if (a[it] < a[u]) return false; if (!check1(it, u)) return false; } return true; } bool check2(int u, int fa) { for (auto it : g[u]) { if (it == fa) continue; if (a[it] > a[u]) return false; if (!check2(it, u)) return false; } return true; }
代码实现
#include<bits/stdc++.h>
using namespace std;
#define ll long long
typedef pair<int, int> PLL;
#define inf 0x3f3f3f3f
const int maxn = 100000 + 10;
int a[maxn];
int vis[maxn];
int wanmei[maxn];
vector<int>g[maxn];
vector<int>root;
bool check1(int u, int fa)
{
for (auto it : g[u])
{
if (it == fa) continue;
if (a[it] < a[u]) return false;
if (!check1(it, u)) return false;
}
return true;
}
bool check2(int u, int fa)
{
for (auto it : g[u])
{
if (it == fa) continue;
if (a[it] > a[u]) return false;
if (!check2(it, u)) return false;
}
return true;
}
bool ans = true;
int check_wanmei(int root, int& f) {//0没有 1一个 2多个
vector<int>x;
for (auto it : g[root]) {
if (!wanmei[it]) {
x.push_back(it);
wanmei[it] = 1;
}
}
if (x.size() == 2) {
int f1, f2;
int dep1, dep2;
dep1 = check_wanmei(x[0], f1);
dep2 = check_wanmei(x[1], f2);
f = f1 + f2;
if (f == 2)ans = false;
//if (abs(dep1 - dep2) > 2)ans = false;
if (dep1 == dep2);
else if (dep1 < dep2) {
if (f == 0)f = 1;
else if (!f1)ans = false;
}
else if (dep1 > dep2) {
if (f == 0)f = 1;
else if (!f2)ans = false;
}
return min(dep1, dep2) + 1;
}
else if (x.size() == 1) {
f = 1;
int ff;
return check_wanmei(x[0], ff);
}
else if (x.size() == 0) {
f = 0;
return 0;
}
return 0;
}
bool check_manzu(int root) {
memset(vis, 0, sizeof(vis));
queue<int>q;
vis[root] = 1;
q.push(root);
q.push(-1);
int flag = 0, flag2 = 0;
while (q.size()) {
int u = q.front();
q.pop();
if (u == -1) {
if (q.size() == 0)break;
if (flag || flag2)break;
q.push(-1);
continue;
}
int num = 0;
for (auto it : g[u]) {
if (!vis[it]) {
num++;
q.push(it);
vis[it] = 1;
}
}
if (num == 1) {
if (flag)return false;
else flag++;
}
else if (num == 0) {
flag2++;
}
}
if (flag > 1)return false;
while (q.size()) {
int u = q.front();
q.pop();
int num = 0;
for (auto it : g[u]) {
if (!vis[it]) {
num++;
q.push(it);
vis[it] = 1;
}
}
if (num != 0)return false;
}
return true;
}
bool check_wanquan(int root) {
memset(wanmei, 0, sizeof(wanmei));
ans = true;
int f;
wanmei[root] = 1;
if(check_manzu(root)){
check_wanmei(root, f);
return ans;
}
else {
return false;
}
}
bool check(int n)
{
if(n<=2)return true;
root.clear();
for (int i = 1; i <= n; i++)
{
if (g[i].size() > 3) return false;
if (g[i].size() == 2) root.push_back(i);
}
if (root.size() > 2) return false;
for (auto it : root) {
if (!check_wanquan(it))continue;
if (check1(it, 0) || check2(it, 0))return true;
}
return false;
}
int main() {
int t;
cin >> t;
while (t--) {
int n;
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> a[i];
g[i].clear();
}
for (int i = 1; i < n; i++) {
int u, v;
cin >> u >> v;
g[u].push_back(v);
g[v].push_back(u);
}
if (check(n))cout << "YES" << endl;
else cout << "NO" << endl;
//if (check_wanquan(1))cout << "YES" << endl;
//else cout << "NO" << endl;
}
}
L3-2 公司员工的日常
前言
求第 k 大,很容易想到的就是权值线段树求总的第 k 大和主席树求区间第 k 大。
方法1:权值线段树+线段树合并
思路分析
考虑每个点的子树都是一棵权值线段树,那么求可以 l o g n logn logn? 求出子树的第 k 大了。如何快速的求出每个结点 u 的子树构成的权值线段树呢?线段树合并即可,将 u 的所有子树的权值线段树合并之后再单点修改增加 u 这个结点信息即可。
实现思路
出题人:杰
- 1.数据保证每个员工能力值不同,并且能力值 <=n ,那么所有员工的能力值其实就是 1-n 的一个排列。由于权值线段树只记录能力值,所以还要先有个数组 id 定位能力值到人 ,也就是 i d [ i ] id[i] id[i]?? 表示能力值为 i 的人的编号。
- 2.权值线段树如何求区间第 k 大?在线段树上二分即可。
- 3.至于线段树合并,其实就是个模板。
代码实现
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+10;
struct edge{
int v,next;
}e[N*2];
int vex[N],tot,k[N],a[N],id[N];
struct Tree{
int l,r,v;
}tree[N*4];
int cnt,n,size[N],root[N],ans[N];
void add(int u,int v){
tot++;
e[tot].v=v;
e[tot].next=vex[u];
vex[u]=tot;
}
void pushup(int now){
tree[now].v=tree[tree[now].l].v+tree[tree[now].r].v;
}
int change(int now,int l,int r,int x,int k) {
if(now==0) now=++cnt;
if(l==r) {
tree[now].v+=k;
return now;
}
int mid=(l+r)/2;
if(x<=mid) tree[now].l=change(tree[now].l,l,mid,x,k);
else tree[now].r=change(tree[now].r,mid+1,r,x,k);
pushup(now);
return now;
}
int merge(int a,int b,int l,int r) {
if(!a) return b;
if(!b) return a;
if(l==r) {
tree[a].v+=tree[b].v;
return a;
}
int mid=(l+r)/2;
tree[a].l=merge(tree[a].l,tree[b].l,l,mid);
tree[a].r=merge(tree[a].r,tree[b].r,mid+1,r);
pushup(a);
return a;
}
int query(int now,int l,int r,int k){
if(l==r)return l;
int mid=(l+r)/2;
if(k<=tree[tree[now].l].v)return query(tree[now].l,l,mid,k);
else return query(tree[now].r,mid+1,r,k-tree[tree[now].l].v);
}
void dfs(int u,int fa){
size[u]=1;
for(int i=vex[u];i;i=e[i].next){
int v=e[i].v;
if(v==fa)continue;
dfs(v,u);
root[u]=merge(root[u],root[v],1,n);
size[u]+=size[v];
}
root[u]=change(root[u],1,n,a[u],1);
ans[u]=id[query(root[u],1,n,k[u])];
}
int main(){
int u;
cin>>n;
for(int i=1;i<=n;i++){
cin>>u;
add(i,u);
add(u,i);
}
for(int i=1;i<=n;i++){
cin>>a[i];
id[a[i]]=i;
}
for(int i=1;i<=n;i++)cin>>k[i];
dfs(1,0);
for(int i=1;i<=n;i++)cout<<ans[i]<<" ";
return 0;
}
方法2:dfs序+主席树
出题人:杰
思路分析
进行 d f s dfs dfs? 序产生的新序列中,每个点的子树都是在该序列中的一段区间。那么问题就变成了 n 次查询新序列的区间第 k 大 。·
实现思路
-
- 1.先 d f s dfs dfs 一遍得到这个 d f s dfs dfs 序
- 2.再以这个 d f s dfs dfs? 序建立主席树
- 3.按顺序对于每个点,用主席树求区间第 k 大即可
代码实现
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+10;
struct edge{
int v,next;
}e[N*2];
int vex[N],tot,k[N],a[N];
struct Tree{
int l,r,v;
}tr[N*4];
int cnt,n,in[N],out[N],root[N],seg[N],id[N],top;
void add(int u,int v){
tot++;
e[tot].v=v;
e[tot].next=vex[u];
vex[u]=tot;
}
void pushup(int now){
tr[now].v=tr[tr[now].l].v+tr[tr[now].r].v;
}
int build(int now,int l,int r){
now=++cnt;
if(l==r){
tr[now].v=0;
return now;
}
int mid=(l+r)/2;
tr[now].l=build(tr[now].l,l,mid);
tr[now].r=build(tr[now].r,mid+1,r);
pushup(now);
return now;
}
int clone(int now){
cnt++;
tr[cnt]=tr[now];
return cnt;
}
int update(int now,int l,int r,int x,int k){
now=clone(now);
if(l==r){
tr[now].v+=k;
return now;
}
int mid=(l+r)/2;
if(x<=mid)tr[now].l=update(tr[now].l,l,mid,x,k);
else tr[now].r=update(tr[now].r,mid+1,r,x,k);
pushup(now);
return now;
}
int query(int l,int r,int nowx,int nowy,int k){
if(l==r)return l;
int sum=tr[tr[nowy].l].v-tr[tr[nowx].l].v;
int mid=(l+r)/2;
if(k<=sum)return query(l,mid,tr[nowx].l,tr[nowy].l,k);
else return query(mid+1,r,tr[nowx].r,tr[nowy].r,k-sum);
}
void solve(){
root[0]=build(0,1,n);
for(int i=1;i<=n;i++)root[i]=update(root[i-1],1,n,a[seg[i]],1);
for(int i=1;i<=n;i++)cout<<id[query(1,n,root[in[i]-1],root[out[i]],k[i])]<<" ";
}
void dfs(int u,int fa){
in[u]=++top;
seg[top]=u;
for(int i=vex[u];i;i=e[i].next){
int v=e[i].v;
if(v==fa)continue;
dfs(v,u);
}
out[u]=top;
}
int main(){
int u;
cin>>n;
for(int i=1;i<=n;i++){
cin>>u;
add(i,u);
add(u,i);
}
for(int i=1;i<=n;i++){
cin>>a[i];
id[a[i]]=i;
}
for(int i=1;i<=n;i++)cin>>k[i];
dfs(1,0);
solve();
return 0;
}
方法3:DFS序+dsu+平衡树
验题人:贝
概述
- 验题人第一反应也是dfs序+主席树,上面出题人写过了,我这边就不赘述了
- 此处验题人给出另一种解法: D F S 序 + d s u + 平 衡 树 DFS序+dsu+平衡树 DFS序+dsu+平衡树
算法思路
- 本题不论是哪一种做法,都有一个核心思想——“子树莫队”
- 莫队做的事情就是按照自己的顺序锁定没每一个询问区间,这里子树就是询问区间,所以叫子树莫队。而且都是离线做法,先将所有询问储存下来,然后再统一处理。
- dsu on tree的思想就体现在,先每次递归计算轻儿子的答案(不加入到平衡树),然后再计算重儿子的答案(加入到平衡树),再将所有轻儿子的贡献加回来计算整棵树的答案
- 如果当前这棵子树不是别人的重儿子,则将他从平衡树中删除
- 概括为轻儿子不保留在平衡树内,重儿子保留在平衡树内
- 总的时间复杂度为 O ( n log ? n ) O(n\log n) O(nlogn)
运行效率
- 可以看一下运行结果,大概只需要不到200毫秒就可以过了
- 但是我们考察的核心还是算法思想,不会特意卡大家常数,就给了1000ms
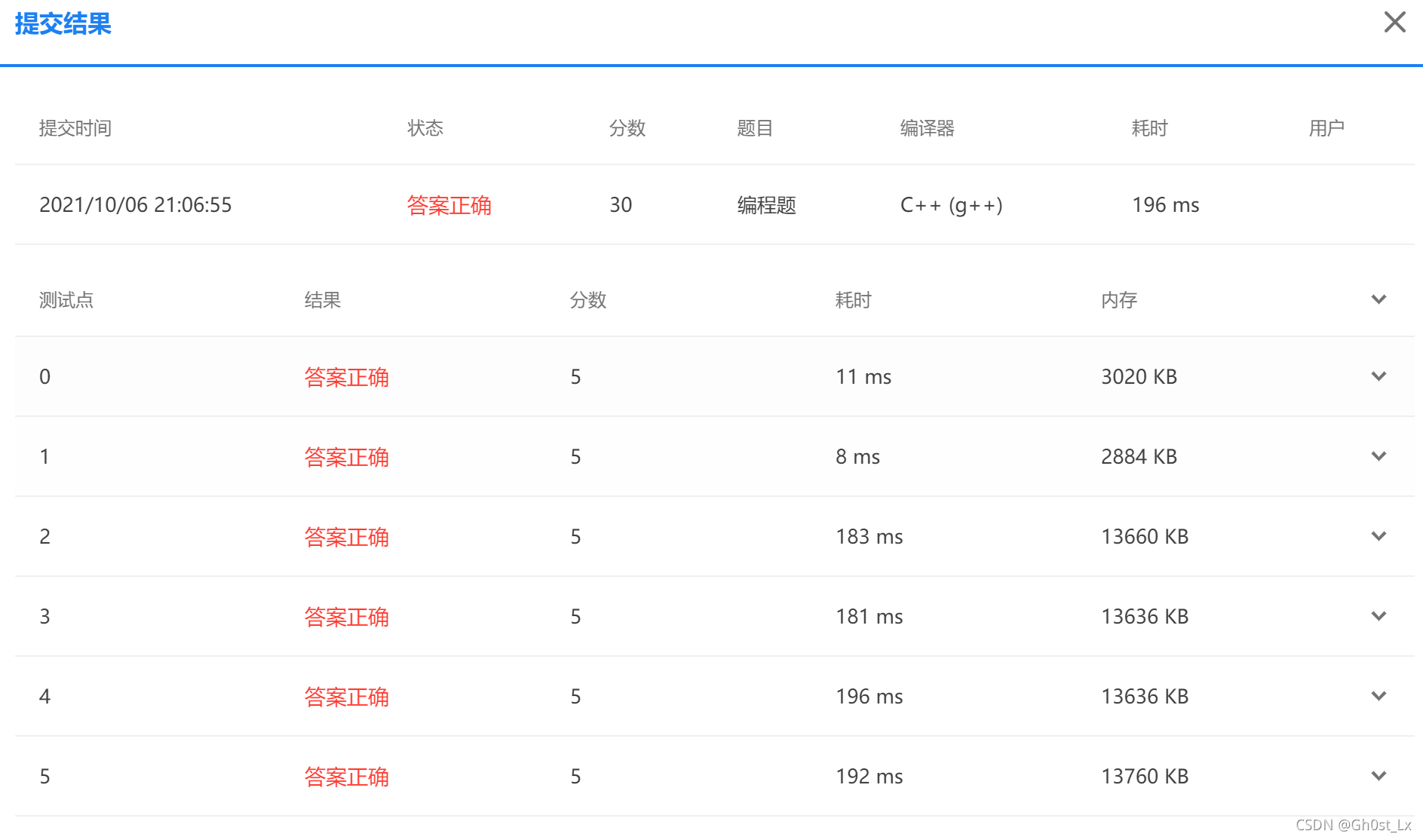
代码实现
#include <bits/stdc++.h>
#include <bits/extc++.h>
#include <unordered_map>
#include <unordered_set>
using namespace std;
using namespace __gnu_cxx;
using namespace __gnu_pbds;
#define debug(x) cerr << #x << ": " << x << '\n'
#define bd cerr << "----------------------" << el
#define el '\n'
#define cl putchar('\n')
#define pb push_back
#define eb emplace_back
#define x first
#define y second
#define rep(i, a, b) for (int i = (a); i <= (b); i++)
#define loop(i, a, b) for (int i = (a); i < (b); i++)
#define dwn(i, a, b) for (int i = (a); i >= (b); i--)
#define ceil(a, b) (a + (b - 1)) / b
#define ms(a, x) memset(a, x, sizeof(a))
#define inf 0x3f3f3f3f
#define db double
typedef long long LL;
typedef long double LD;
typedef pair<int, int> PII;
typedef pair<db, db> PDD;
typedef vector<int> vci;
inline int read()
{
int f = 1, d = 0;
char ch;
ch = getchar();
while (ch < '0' || ch > '9')
{
if (ch == '-')
f = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9')
d = (d << 1) + (d << 3) + (ch ^ 48), ch = getchar();
return d * f;
}
const int N = 1e5 + 10, M = 2e6 + 10, E = 1e3 + 10, md = 1e9 + 7;
const double PI = acos(-1), eps = 1e-8;
int T, n, m, k;
LL a[N];
vector<int> g[N];
int qry[N], ans[N];
typedef tree<PII, null_type, less<PII>, rb_tree_tag, tree_order_statistics_node_update> Tree;
Tree tr;
int dfn[N], iDfn[N], sz[N], son[N], dfs_clock;
void merge(int cur, bool isSon)
{
for (int ver : g[cur])
if (ver != son[cur])
merge(ver, false);
if (son[cur]) //如果重儿子存在
merge(son[cur], true);
for (int ver : g[cur])
if (ver != son[cur])
for (int i = dfn[ver]; i < dfn[ver] + sz[ver]; i++)
tr.insert(make_pair(a[iDfn[i]], iDfn[i]));
tr.insert(make_pair(a[cur], cur));
ans[cur] = (*tr.find_by_order(qry[cur] - 1)).second;
if (!isSon) //如果不是重儿子
for (int i = dfn[cur]; i < dfn[cur] + sz[cur]; i++)
tr.erase(make_pair(a[iDfn[i]], iDfn[i]));
}
void dfs(int cur, int pre) //生成dfs序
{
dfn[cur] = ++dfs_clock;
iDfn[dfs_clock] = cur;
sz[cur] = 1;
for (int ver : g[cur])
{
dfs(ver, cur);
sz[cur] += sz[ver]; //计算当前子树的大小
if (!son[cur] || sz[ver] > sz[son[cur]])
son[cur] = ver; //寻找重儿子
}
}
int main()
{
cout.tie(0);
n = read();
rep(i, 1, n)
{
k = read();
g[k].pb(i);
}
rep(i, 1, n)
a[i] = read();
rep(i, 1, n)
qry[i] = read();
dfs(1, 0); //获取dfs序
merge(1, 1); //默认1也是重儿子,省略最后一次删除,优化
for (int i = 1; i <= n; i++)
cout << ans[i] << ' ';
}
L3-3 三元组
出题人:贝
出题者报告
- 原本这题我放的是一道送命题,强行写暴力也得需要较深厚的算法水平(maybe校选第一水平?),70分钟左右才能搞出来5分,正解的话,给题解的话也是不会做的那种。
- 但是后来我还是把那题给换掉了,毕竟现在是ABC出题组掌权,不是以难倒大家为目标,而是为了出一份高质量的卷子,具有区分度。
- 所以我换成了这一道,至于原本那题我拿到后续的给大家。
- 我设置了四个测试点
- 测试点1: n 1 = n 2 = n 3 = 50 n_1=n_2=n_3=50 n1?=n2?=n3?=50,三方暴力可以过,2分
- 测试点2: n 1 = 100 , n 2 = 1000 , n 3 = 1 e 5 n_1=100,n_2=1000,n3=1e5 n1?=100,n2?=1000,n3=1e5,mutiset可以过,5分
- 测试点3: n 1 = 32343 , n 2 = 50097 , n 3 = 96675 n_1=32343,n_2 = 50097,n_3=96675 n1?=32343,n2?=50097,n3?=96675,FFT可以过,11分
- 测试点4: n 1 = n 2 = n 3 = 1 e 5 n1=n2=n3=1e5 n1=n2=n3=1e5,FFT可以过,卡掉没开long long的情况(WA),以及常数过大的FFT模板(TLE),12分。
算法思路
算法一:三次方暴力,2分
- 没啥好说的,无脑三个循环枚举
- 时间复杂度 O ( n 3 ) O(n^3) O(n3)
代码实现
#define el '\n'
#define rep(i, a, b) for (int i = (a); i <= (b); i++)
int main()
{
cin.tie(0);
cout.tie(0);
cin >> n1;
rep(i, 1, n1)
cin >> a[i];
cin >> n2;
rep(i, 1, n2)
cin >> b[i];
cin >> n3;
rep(i, 1, n3)
cin >> c[i];
LL cnt = 0;
rep(i, 1, n1)
rep(j, 1, n2)
rep(k, 1, n3)
if(a[i] + b[j] + c[k] == 0)
cnt ++ ;
cout << cnt << el;
}
算法二:multiset,7分
- 因为数组自身内部可能存在相同值,所以要用
multiset,假如只有对于两个数组而言,我们如何用mutiset?
*找相反数! - 所以我们也可以 n 2 n^2 n2放入 m u l t i s e t multiset multiset中,然后进行查找
- 我hint中给出范围就是方便选手,将那两个数组放入
multiset中,因为有n1*n2==n3
复杂度分析
- 时间复杂度,将 a , b a,b a,b数组里面的元素插入 m u l t i s e t multiset multiset中需要 n 1 × n 2 n_1\times n_2 n1?×n2?次,查询共需要 n 3 n_3 n3?次,插入和查询的操作每次都为 O ( log ? ( n 1 × n 2 ) ) O(\log (n_1\times n_2)) O(log(n1?×n2?)),总得时间复杂度为 O ( n 1 × n 2 × log ? ( n 1 × n 2 ) + n 3 log ? ( n 1 × n 2 ) ) O(n_1 \times n_2 \times \log (n_1\times n_2) + n_3 \log (n_1 \times n_2)) O(n1?×n2?×log(n1?×n2?)+n3?log(n1?×n2?))
- 当然题目最后我给出数据,这边 m u l t i s e t multiset multiset放的是 n 1 , n 2 n_1,n_2 n1?,n2?因为题目中有个数据 n 1 × n 2 = n 3 n_1\times n_2 =n_3 n1?×n2?=n3?,也是希望某些一队种子选手能算出复杂度来(原本我是打算放 n 1 , n 3 n_1,n_3 n1?,n3?的,因为人的惯性思维就是习惯放两个连续的 n 1 , n 2 n_1,n_2 n1?,n2?或者 n 2 , n 3 n_2,n_3 n2?,n3?这样这7分也很难拿了,最后我还是没那样搞,暴力分的难度降低了一点,不然只有一队的种子选手才能算出对应的复杂度拿到这暴力的7分)
代码实现
multiset<int> s;
#define rep(i, a, b) for (int i = (a); i <= (b); i++)
#define el '\n'
int main()
{
cin.tie(0);
cout.tie(0);
cin >> n1;
rep(i, 1, n1)
cin >> a[i];
cin >> n2;
rep(i, 1, n2)
cin >> b[i];
cin >> n3;
rep(i, 1, n3)
cin >> c[i];
rep(i, 1, n1)
rep(j, 1, n2)
s.insert(a[i]+b[j]);
LL cnt = 0;
rep(i, 1, n3)
cnt += s.count(-c[i]);
cout << cnt << el;
}
算法三:快速傅里叶变换FFT,30分
- 这题不打算给人A,毕竟本来会FFT的咱们学校也屈指可数
- 更何况是IOI赛制没有纸质材料,也符合L3-3对于我们学校水平的定位
- 最不可思议的是,何大佬现场居然A掉了orz orz
- 如果不懂得FFT的可以自行百度,百度上很多学习博客,这边就不赘述了
- 这题关键的思路为:桶
- FFT是处理多项式乘法的
- 我们都知道FFT可以将多项式乘法 O ( n 2 ) O(n^2) O(n2)加速为 O ( n log ? n ) O(n \log n) O(nlogn)
- 那么两个数的关系是相加的,如何让他变成相乘的呢?把他们都放在指数上面,两个幂指数相乘,指数相加。
- 这样的话做两次FFT就可以A了,值得注意的是,因为有负数的存在,故要整体平移,最小的情况是三个
-1e5所以0代表的是-3e5,而真正的0则是3e5
复杂度分析
- 时间复杂度,为FFT的复杂度, O ( n log ? n ) O(n \log n) O(nlogn)级别
代码实现
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
const int N = 600010 * 2;
const double PI = acos(-1);
int n, m;
struct Complex
{ //复数结构体,基本不会有任何变动
double x, y;
Complex operator+(const Complex &t) const
{
return {x + t.x, y + t.y};
}
Complex operator-(const Complex &t) const
{
return {x - t.x, y - t.y};
}
Complex operator*(const Complex &t) const
{
return {x * t.x - y * t.y, x * t.y + y * t.x};
}
} A[N], B[N], C[N];
int rev[N], bit, tot;
void fft(Complex a[], int inv)
{ //inv表示转序列化方向,1为从系数表示法变成点值表示法,-1则反过来;
for (int i = 0; i < tot; i++)
if (i < rev[i])
swap(a[i], a[rev[i]]);
for (int mid = 1; mid < tot; mid <<= 1)
{
auto w1 = Complex({cos(PI / mid), inv * sin(PI / mid)});
for (int i = 0; i < tot; i += mid * 2)
{
auto wk = Complex({1, 0});
for (int j = 0; j < mid; j++, wk = wk * w1)
{
auto x = a[i + j], y = wk * a[i + j + mid];
a[i + j] = x + y, a[i + j + mid] = x - y;
}
}
}
}
void in(int len, Complex a[])
{
for (int i = 1; i <= len; ++i)
{
int num;
scanf("%d", &num);
a[num + 100000].x += 1.0;
}
}
void _merge(Complex a[], Complex b[], int &n, int &m)
{
bit = 0;
while ((1 << bit) < n + m + 1)
bit++;
tot = 1 << bit;
n = tot;
rev[0] = 0; //初始化rev
for (int i = 0; i < tot; i++)
rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (bit - 1));
fft(a, 1), fft(b, 1);
for (int i = 0; i < tot; i++)
a[i] = a[i] * b[i];
fft(a, -1);
//上面都是板子不用改,只需要加一个bit=0的初始化即可
for (int i = 0; i < tot; ++i)
a[i].x = 1.0 * (long long)(a[i].x / tot + 0.5);
}
int main()
{
//int k;scanf("%d",&k);//找到三元组和为k的方案数;
int lena;
scanf("%d", &lena);
in(lena, A);
int lenb;
scanf("%d", &lenb);
in(lenb, B);
int lenc;
scanf("%d", &lenc);
in(lenc, C);
//input finished
lena = lenb = lenc = 200000; //取值范围就是多项式长度,2e5个桶,下标的问题,负数需要右移
_merge(A, B, lena, lenb); //合并
_merge(A, C, lena, lenc); //合并
//solved
printf("%lld", (long long)(A[300000].x)); //因为最小值可能为三个-1e5之和,需要将桶右移
return 0;
}
/*
1
2
2
-2 -1
2
1 0
*/