[数据结构与算法]1、递归算法解决汉诺塔问题（算法基础）

1、递归算法的特点

1、调用本身
2、设置一个结束条件

需要先将问题简单化，找到一个可以不断递推下去的规律

2、问题背景：

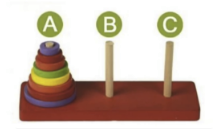
相传在古印度圣庙中，有一种被称为汉诺塔(Hanoi)的游戏。该游戏是在一块铜板装置上，有三根杆(编号A、B、C)，在A杆自下而上、由大到小按顺序放置64个金盘(如图1)。
游戏的目标：把A杆上的金盘全部移到C杆上，并仍保持原有顺序叠好。
操作规则：每次只能移动一个盘子，并且在移动过程中三根杆上都始终保持大盘在下，小盘在上，操作过程中盘子可以置于A、B、C任一杆上。

3、问题：如何模拟这个移动的过程

4、解题核心思路：

假设金盘有n个，那么我们可以看成两部分：最底下的1个和上面的n-1个金盘。
问题就被简化成：移动两部分。

移动两部分的步骤可以拆解为以下三步：
1、把n-1个盘子从A经过C移动到B；（多个盘子想移动到B柱，必须经过C柱才行）
2、把第n个盘子从A移动到C；
3、把n-1个盘子从B经过A移动到C；

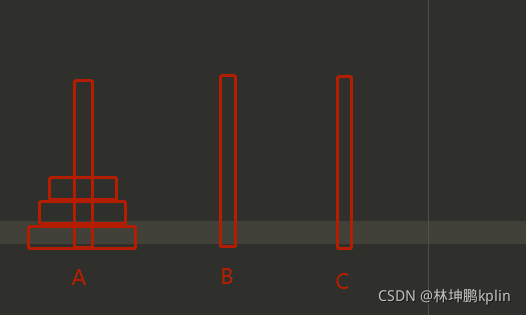
5、推演

假设n=3，我们可以根据下图，推演一遍，是否符合这个规律

6、代码：

def hanoi(n, a, b, c):   # 参数n代表有n个盘子，a, b, c分别代表3个柱子
    if n > 0:
        hanoi(n-1, a, c, b)
        print('moving from %s to %s'%(a, c))
        hanoi(n-1, b, a, c)

hanoi(3, 'A', 'B', 'C')

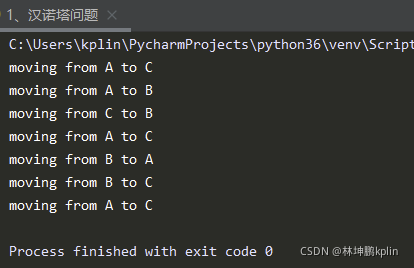
7、输出结果：