1.1 数据结构介绍

数据结构是为实现对计算机数据有效使用的各种数据组织形式，服务于各类计算机操作。
概念这么给的，其实我觉得还有点抽象，，就拿我们生活中的楼来讲，它为什么是向上堆上去的，它咋不散开来盖房呢？在这个拥挤的城市里，要想容纳更多的人住在这，那自然要这么建了。而楼一定有完善的结构才能实现稳定和大容量。
同样的，我们的计算机的内存的容量跟城市一样是空间有限的，用于运算的大量的数据当然需要有一个排列的结构才能更好的发挥内存的性能。
所以，数据结构旨在降低各种算法计算的时间与空间复杂度，以达到最佳的任务执行效率。

1.1.2 常见数据结构

常见的数据结构可分为「线性数据结构」与「非线性数据结构」，具体为：「数组」、「链表」、「栈」、「队列」、「树」、「图」、「散列表」、「堆」。
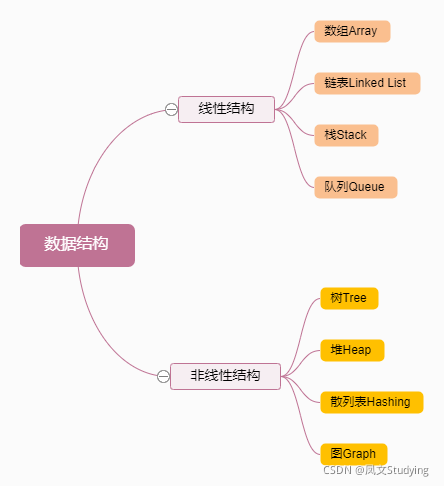
在这里插入图片描述
每一种数据结构都有着独特的数据存储方式，也有它们的各自的结构和优缺点。

1.1.3 抽象数据类型（ADT）

抽象数据类型（abstract data type,ADT）是带有一组操作的一些对象的集合。
首先它是一些对象的集合，这里的对象就是某个数据类型对应的具体值，如int，string都叫数据类型，而这个具体值，比如3，“医信”，这些具体的数值和字符都可以叫作对象。由于部分学弟学妹还刚接触甚至不了解面向对象相关知识，所以这里解释得这么详细。
其次它带有一组操作，在ADT的定义中没有地方提到关于这组操作是如何实现的任何解释。拿集合来说，可以有像添加（add）、删除（remove）以及包含（contain）这样一些操作。再比如链表，使链表的容量增加或减少，使添加一个元素或减少一个元素，使某两个元素换一下位置，这些针对同一链表的操作合起来就可以称作一组操作。
所以，诸如表、数组、集合、图等数据结构以及它们各自的操作一起形成的这些对象都可以被看做是抽象数据类型，这就像整数、实数、布尔数都是数据类型一样。最后我自己总结就是 ADT=某一种数据结构+对应的操作集合。

1.2 线性结构

线性结构是什么？
数据结构中线性结构指的是 数据元素之间存在着“一对一”的线性关系的数据结构。 线性结构是一个有序数据元素的集合。

这里的一对一关系意思是，每一个元素之间是首尾相接的，字面意思就是元素之间连成一条线。 当然，第一个元素和最后一个元素就不能连在一起了，否则就成了一个环了。
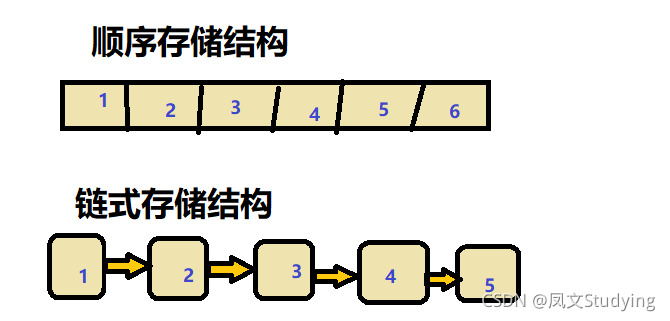
在这里插入图片描述
以上这两个都是线性结构，顺序表的数据在内存中的存储是连续的（靠在一起的，如数组就是这个特点），而链表的存储不一定是连续的，每个元素依靠自身节点中存放的相邻元素的地址信息来找到下一个元素。需要知道的是，不管是顺序存储还是链式存储都是元素之间连成一条线。

那么总结一下线性结构的特点：
线性结构有唯一的首元素（第一个元素）
线性结构有唯一的尾元素（最后一个元素）
除首元素外，所有的元素都有唯一的“前驱”
除尾元素外，所有的元素都有唯一的“后继”
数据元素之间存在“一对一”的关系，即除了第一个和最后一个数据元素之外，其它数据元素都是首尾相接的。

1.2.1 数组（Array）

数组是可以再内存中连续存储多个元素的结构，在内存中的分配也是连续的，数组中的元素通过数组下标进行访问，数组下标从0开始。
代码实现：

// 初始化一个长度为 5 的数组 array
int[] array = new int[5];
// 元素赋值
array[0] = 2;
array[1] = 3;
array[2] = 1;
array[3] = 0;
array[4] = 2;

优点：
1、按照索引访问元素速度快
2、按照索引遍历数组方便

缺点：
1、数组的大小固定后就无法扩容了
2、数组只能存储一种类型的数据
3、添加，删除的操作慢，因为要移动其他的元素。
就比如，你想要在索引为0的位置（首位置）添加一个元素，由于数组大小固定无法直接扩容，你只能创建一个比原数组容量大一个空间的新数组，然后把第一个数组放进去，再把原数组的元素挨个放到新数组里面。这一套过程下来，速度慢的一批！等会你看到链表的介绍你就会发现链表在方面的优势。

适用场景：
频繁查询，对存储空间要求不大，很少增加和删除的情况。

1.2.2 链表（Linked List）

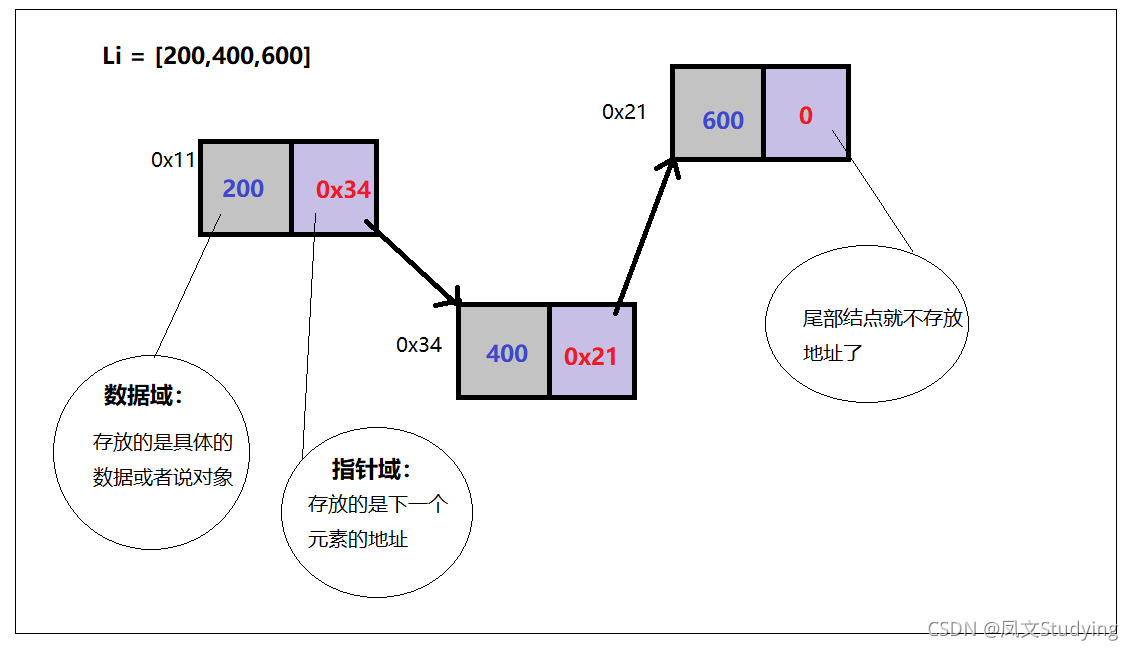
链表是物理存储单元上非连续的、非顺序的存储结构（链式），数据元素的逻辑顺序是通过链表的指针地址实现，每个元素包含两个结点，一个是存储元素的数据域 (内存空间)，另一个是指向下一个结点地址的指针域。
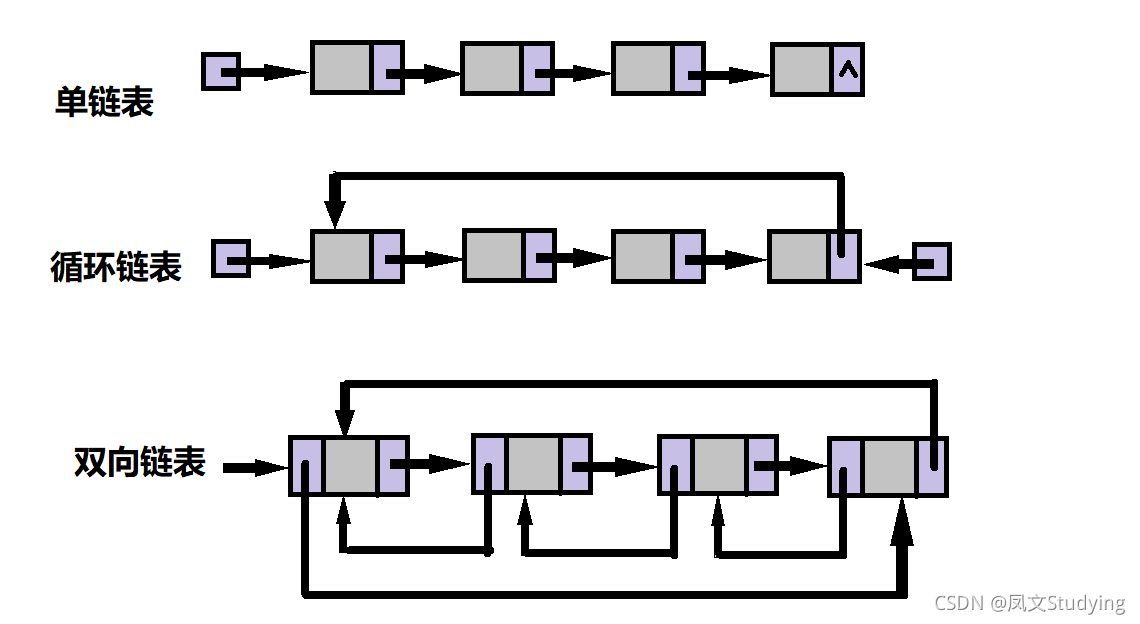
在这里插入图片描述根据指针的指向，链表能形成不同的结构，例如单链表，双向链表，循环链表等。

代码实现：
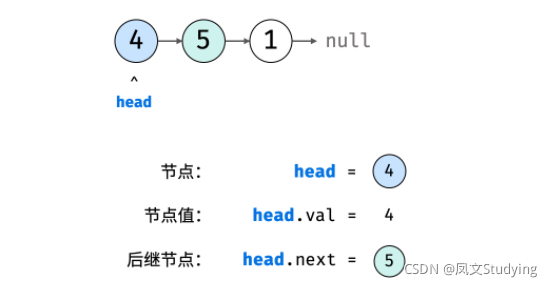
链表以节点为单位，每个元素都是一个独立对象，在内存空间的存储是非连续的。链表的节点对象具有两个成员变量：「值 val」，「后继节点引用 next」。

class ListNode {
    int val;       // 节点值
    ListNode next; // 后继节点引用
    ListNode(int x) { val = x; }
}

如下图所示，建立此链表需要实例化每个节点，并构建各节点的引用指向。

// 实例化节点
ListNode n1 = new ListNode(4); // 节点 head
ListNode n2 = new ListNode(5);
ListNode n3 = new ListNode(1);

// 构建引用指向
n1.next = n2;
n2.next = n3;

在这里插入图片描述

链表的优点：
链表不需要初始化容量，因为是它是一种无序的组织，所以可以任意加减元素；添加或者删除元素时只需要改变前后两个元素结点的指针域指向地址即可，所以添加，删除效率高；

缺点：
因为含有大量的指针域，占用空间较大；
查找元素需要遍历链表来查找，非常耗时。

适用场景：
数据量较小，需要频繁增加，删除操作的场景。

现在来看，貌似它的特性跟数组正好相反，所以呢，我们在写算法的时候，根据需求，应该选择合适的存储方式。这里总结一下，数组访问遍历快，增删慢；链表增删快，访问遍历慢。

1.2.2 栈（Stack）

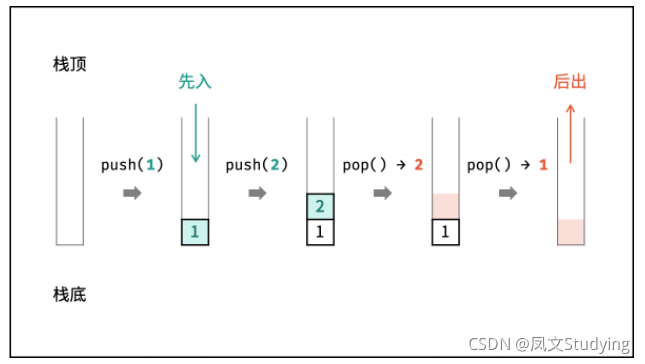
栈是一种特殊的线性表，仅能在线性表的一端操作，栈顶允许操作，栈底不允许操作。栈的特点是：先进后出，或者说是后进先出，从栈顶放入元素的操作叫入栈，取出元素叫出栈。

栈的结构就像一个集装箱，越先放进去的东西越晚才能拿出来，所以，栈常应用于实现递归功能方面的场景，例如斐波那契数列。
在这里插入图片描述
代码实现：

Stack<Integer> stack = new Stack<>();
LinkedList<Integer> stack = new LinkedList<>();

stack.addLast(1);   // 元素 1 入栈
stack.addLast(2);   // 元素 2 入栈
stack.removeLast(); // 出栈 -> 元素 2
stack.removeLast(); // 出栈 -> 元素 1

1.2.3 队列（Queue）

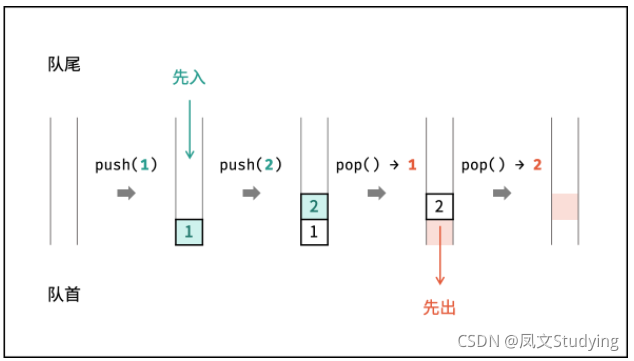
队列与栈一样，也是一种线性表，不同的是，队列可以在一端添加元素，在另一端取出元素，也就是：先进先出。从一端放入元素的操作称为入队，取出元素为出队。
队列也好理解，就跟它的名字一样，比如你中午去食堂干饭，有时候去了不能直接打饭，需要排队，而你排队需要遵循一个规则，就是只能去这个队的队尾去排队，这个就是入队，等你这排的第一个人打完饭了，那么这个人就可以从队首离开了，这个就是出队，接着后面的人依次顶替上来，直到轮到你在队首时才能离开。所以呢，先到的可以先打饭，先离开。

示例图如下：
在这里插入图片描述
代码实现：
队列是一种具有先进先出特点的抽象数据结构，可使用链表实现。

Queue<Integer> queue = new LinkedList<>();

queue.offer(1); // 元素 1 入队
queue.offer(2); // 元素 2 入队
queue.poll();   // 出队 -> 元素 1
queue.poll();   // 出队 -> 元素 2