前言

本文用于记录准备数学建模比赛时的算法学习，由于时间有限，算法原理及数学推导不再赘述，仅记录实现代码以及细节。

一、层次分析法

建模比赛中最基础的模型之一，其主要用于解决评价类问题（例如：选择哪种方案最好、哪位运动员或者员工表现的更

%评价矩阵 由专家评估给出
%一致矩阵
data_std =[1 2 5;
           1/2 1 2;
           1/5 1/2 1];
%不一致矩阵
data2 =[1 2 5;
        1/2 1 2;
        1/4 1/2 1];
n = 3; %n阶段方阵
E = eig(data_std);%获得特征值
 [V,D]=eig(data_std); %V为特征向量 按列
E2 = eig(data2);
Em = max(E);  %n阶正互反矩阵一致矩阵时 最大特征值Em = n
Em2 = max(E2); %不一致 Em>n
CI_std = (Em - n)/(n-1);%一致性指标
%查找平均随机一致性指标RI
RI = 0.52;
CI_2 = (Em2 - n)/(n-1);
CR_std = CI_std/RI; %一致性比例
CR_2 = CI_2/RI;
%如果CR < 0.1, 则可认为判断矩阵的一致性可以接受；否则需要对判断矩阵进行修正
%判断矩阵权重计算
%方法1 算术平均法求权重
%step1 按列归一化
weight_std = zeros(size(data_std));
sum_1 = sum(data_std,1);
sum_2 = sum(data_std,2);
for i = 1:n
    
    for j = 1:n
        weight_std(i,j) = data_std(i,j)/sum_1(1,j);
    end
end
%step2 按行求和取平均 得到权重向量
weight_vector = sum(weight_std,2)/n;

%方法2 几何平均法
%第一步：将A的元素按照行相乘得到一个新的列向量
weight_02 = ones(n,1);
for i = 1:n
    for j = 1:n
        weight_02(i,1) = weight_02(i,1)*data_std(i,j);
    end
end
%第二步：将新的向量的每个分量开n次方
weight_02 = power(weight_02 , 1/n);
%第三步：对该列向量进行归一化即可得到权
weight_vector_02 = ones(size(weight_02));
for i = 1:n
    weight_vector_02 = weight_02/sum(weight_02,1);
end

%特征向量法
%第一步：求出矩阵A的最大特征值以及其对应的特征向量
[m,index] = max(E);
%第二步：对求出的特征向量进行归一化即可得到我们的权重
weight_vector_03 = ones(size(weight_02));
V_sum = sum(V,1);
for i = 1:n
    weight_vector_03(i,1) = V(i,index)/V_sum(1,index);
end
%得到的权重矩阵
res = cat(2,weight_vector,weight_vector_02,weight_vector_03);

二、K-means聚类

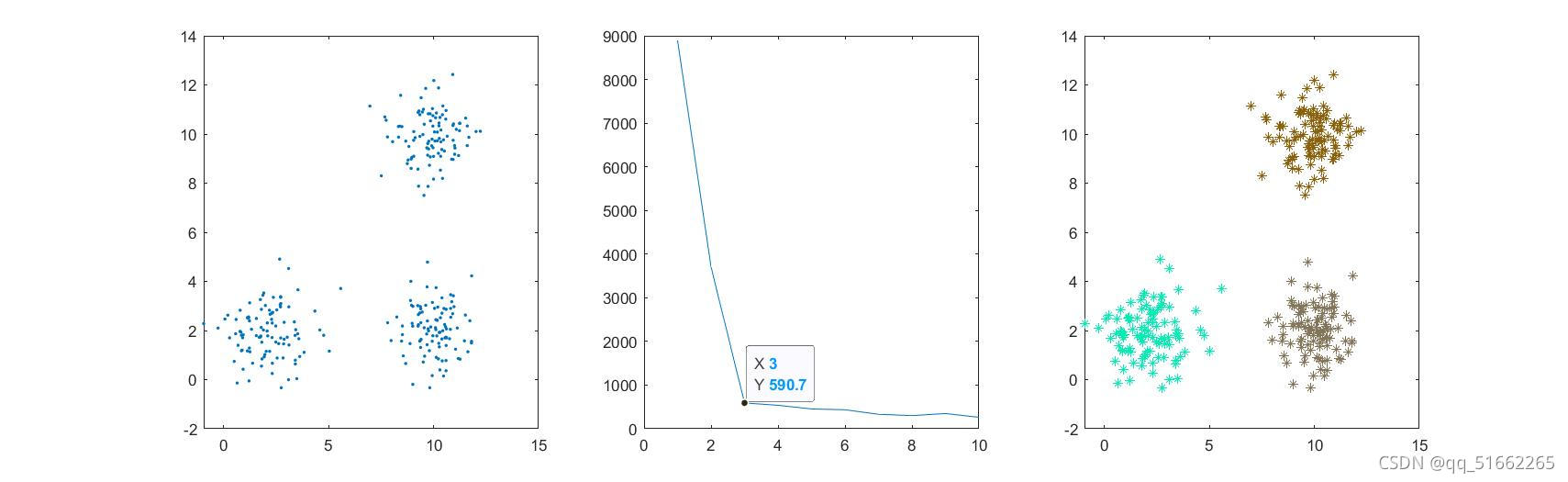
常用的聚类算法，可以将数据分为n类，参数n需要自己设置。可通过手肘法确定合适的n的大小。

%高斯分布 生成聚类数据
Category1=[normrnd(2,1,100,2)]; %高斯分布的第一类数据集合
Category2=[normrnd(10,1,100,2)];%第二类
Category3=[normrnd(2,1,100,2)];%第三类

for i=1:100
    Category3(i,1)= Category3(i,1)+8;
end
data = cat(1,Category1,Category2,Category3);%矩阵拼接
subplot(1,3,1);
plot(data(1:300,1),data(1:300,2),'.');
SSE = zeros(1,10);
for k = 1:10 %手肘法确定K值 
    [ldx,C]=kmeans(data,k); %ldx为分类点 C为中心点坐标
    for i = 1:size(data,1)
        for j = 1:size(data,2)
            SSE(k)  = SSE(k) + power((data(i,j) - C(ldx(i),j)),2) ;
        end
    end
end
subplot(1,3,2);
plot(1:10,SSE);
k = 3;

%确定K值 = 3后绘图
[ldx,C]=kmeans(data,k); %ldx为分类点 C为中心点坐标
for i = 1:size(data,1)
    rand('seed',ldx(i,1));
    color = rand(1,3);
    subplot(1,3,3);
    plot(data(i,1),data(i,2),'*','color',color);
    hold on;
end

运行结果:

三、支持向量机（SVM）

支持向量机（Support Vector Machine, SVM）是一类按监督学习（supervised learning）方式对数据进行二元分类的广义线性分类器（generalized linear classifier），其决策边界是对学习样本求解的最大边距超平面（maximum-margin hyperplane。可用于分类器，对数据进行二元分类。

%高斯分布 生成聚类数据
Category1=[normrnd(2,1,100,2)]; %高斯分布的第一类数据集合
Category2=[normrnd(10,1,100,2)];%第二类
Category3=[normrnd(2,1,100,2)];%第三类
te = ones(10,1);
te = te +1;
for i=1:100
    Category3(i,1)= Category3(i,1)+8;
end
%数据处理，增加标号，抽出[91:100]作为待分类
train_data = cat(1,Category1(1:90,1:2),Category3(1:90,1:2));
test_data = cat(1,Category1(91:100,1:2),Category3(91:100,1:2));
train_index = cat(1,ones(90,1),ones(90,1)+1);%已知样本标号
test_index = cat(1,ones(10,1),ones(10,1)+1);
[data_std,ps] = mapstd(train_data');%训练集标准化  Z-Score  逐行标准化
test_std = mapstd('apply',test_data',ps); %利用训练数据中均值和方差进行处理
SVMModel = fitcsvm(data_std',train_index,'KernelFunction','linear'); %训练支持向量机分类器
[lable,score]=predict(SVMModel,data_std');
classification=predict(SVMModel,test_std');%预测结果

num = 0;
for i = 1:size(classification,1)
    if classification(i,1) ==  test_data(i,1)
        num = num+1;
    end
end
err_rate = num/size(classification,1); %计算误差
classOrder = SVMModel.ClassNames;

sv = SVMModel.SupportVectors; %支持向量
figure
data_std = data_std';
gscatter(data_std(:,1),data_std(:,2))
hold on
plot(sv(:,1),sv(:,2),'ko','MarkerSize',10)
legend('versicolor','virginica','Support Vector')
hold off

运行结果: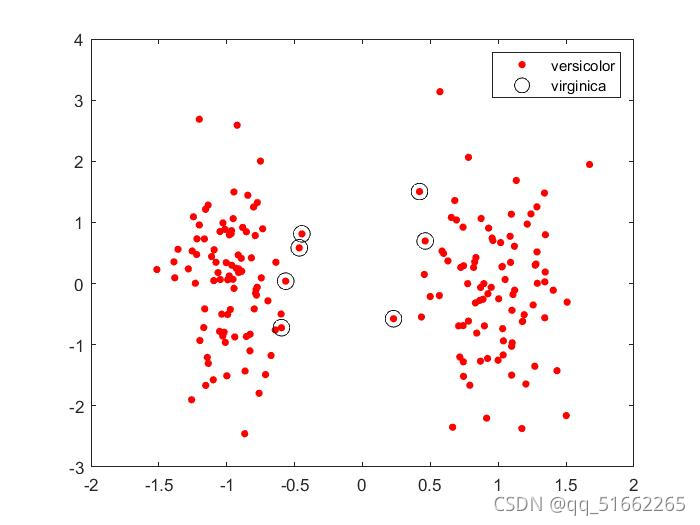 在这里插入图片描述

四、熵权法

按照信息论基本原理的解释，信息是系统有序程度的一个度量，熵是系统无序程度的一个度量；根据信息熵的定义，对于某项指标，可以用熵值来判断某个指标的离散程度，其信息熵值越小，指标的离散程度越大，该指标对综合评价的影响（即权重）就越大，如果某项指标的值全部相等，则该指标在综合评价中不起作用。因此，可利用信息熵这个工具，计算出各个指标的权重，为多指标综合评价提供依据。为不同指标计算权重.

x = xlsread('123.xlsx');

ind = ones(size(x,2),1);%正向写1，负向写2

[n,m]=size(x); % n个样本, m个指标 %%数据的归一化处理
for i=1:m 
    if ind(i)==1 %正向指标归一化 
        X(:,i)=guiyi(x(:,i),1,0.002,1); %若归一化到[0,1], 0会出问题 
    else %负向指标归一化 
        X(:,i)=guiyi(x(:,i),2,0.002,1); 
    end
end
%%计算第j个指标下，第i个样本占该指标的比重p(i,j)
p = ones(size(x));
for i=1:n 
    for j=1:m 
        p(i,j)=X(i,j)/sum(X(:,j)); 
    end
end
%%计算第j个指标的熵值e(j) 
e = ones(1,size(x,2));
k=1/log(n); 
for j=1:m 
    e(j)=-k*sum(p(:,j).*log(p(:,j)));
end
d=ones(1,m)-e; %计算信息熵冗余度 
w=d./sum(d); %求权值w
s=X*w'; %求综合得分

function y=guiyi(x,type,ymin,ymax) 
%实现正向或负向指标归一化，返回归一化后的数据矩阵 
%x为原始数据矩阵, 一行代表一个样本, 每列对应一个指标
%type设定正向指标1,负向指标2 
%ymin,ymax为归一化的区间端点 
[n,m]=size(x); 
y=zeros(n,m);
xmin=min(x); 
xmax=max(x); 
switch type 
    case 1 
        for j=1:m 
            y(:,j)=(ymax-ymin)*(x(:,j)-xmin(j))/(xmax(j)-xmin(j))+ymin; 
        end
    case 2 
        for j=1:m 
            y(:,j)=(ymax-ymin)*(xmax(j)-x(:,j))/(xmax(j)-xmin(j))+ymin; 
        end
end