二叉树
1.定义
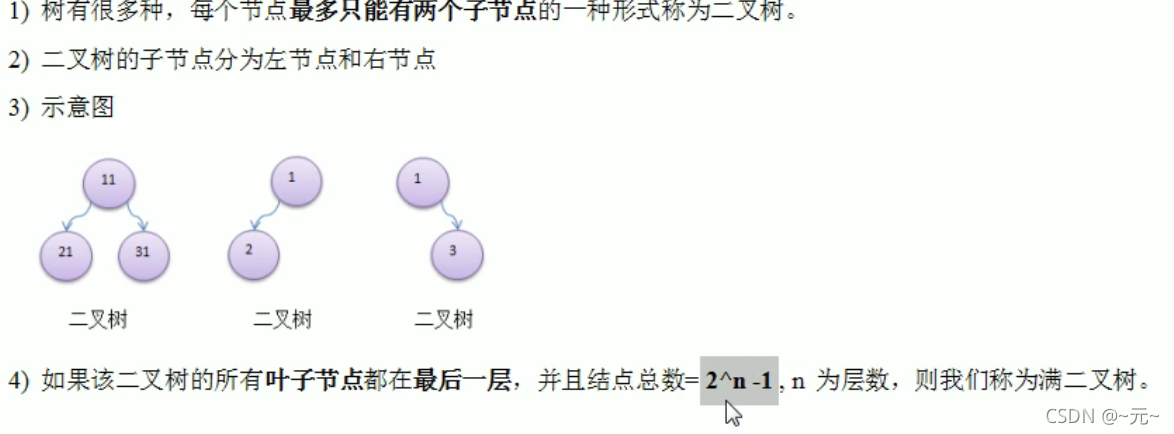
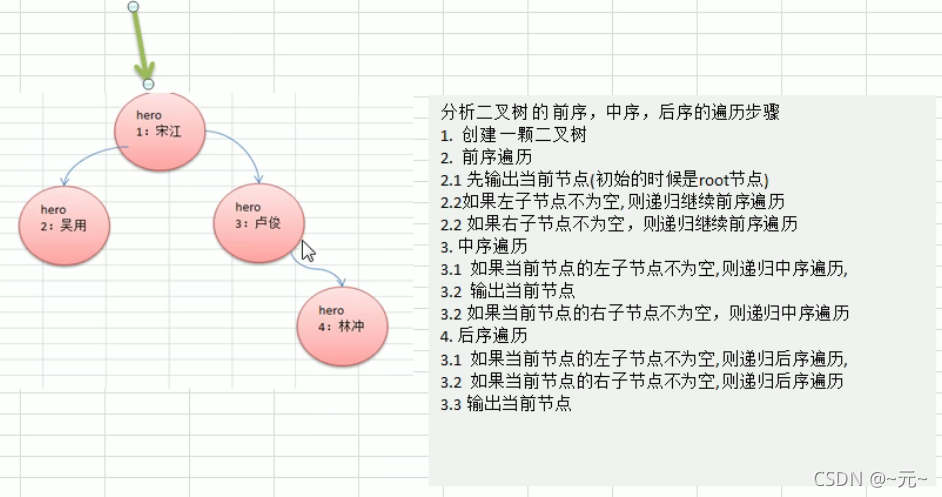
前序中序后序遍历的概念解析

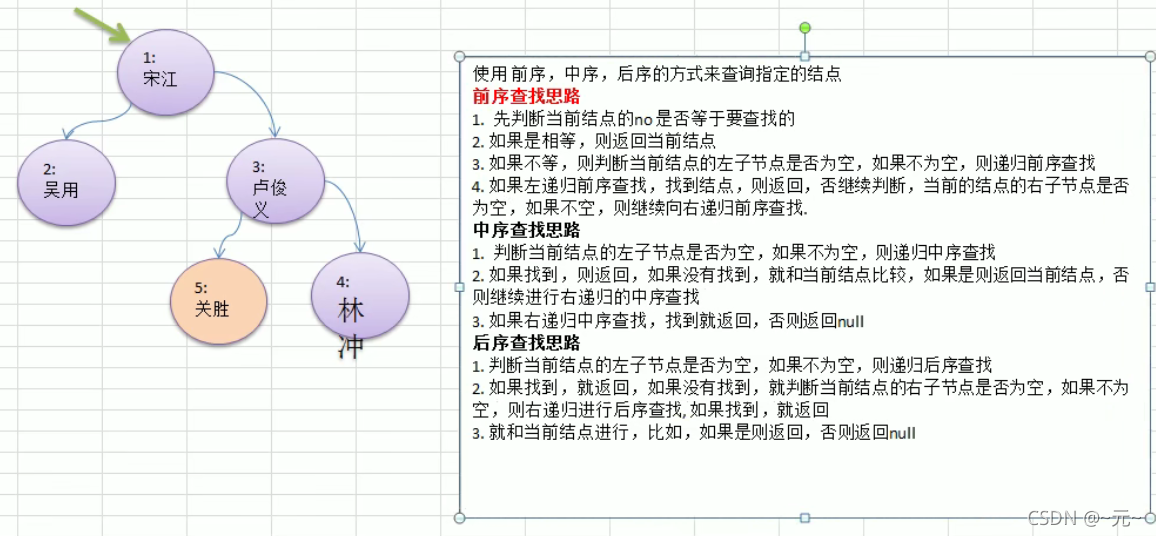
使用前序、中序、后序的方式来查询指定的节点
package com.atyuan.tree;
/**
* @program: DataStructures
* @description: 二叉树
* @author: yuan
* @create: 2021-10-18 21:05
**/
public class BinaryTreeDemo {
public static void main(String[] args) {
//创建二叉树
BinaryTree binaryTree = new BinaryTree();
//创建节点
HeroNode h1 = new HeroNode(1,"吴用");
HeroNode h2 = new HeroNode(2,"宋江");
HeroNode h3 = new HeroNode(3,"卢俊义");
HeroNode h4 = new HeroNode(4,"林冲");
HeroNode h5 = new HeroNode(5, "鲁达");
//先手动创建二叉树
binaryTree.setRoot(h1);
h1.setLeft(h2);
h1.setRight(h3);
h3.setLeft(h5);
h3.setRight(h4);
// System.out.println("前序遍历:");
// binaryTree.preOrder();
// System.out.println("=====================");
// System.out.println("中序遍历:");
// binaryTree.infixOrder();
// System.out.println("=====================");
// System.out.println("后序遍历:");
// binaryTree.postOrder();
/*
//前序遍历
System.out.println("前序遍历方式");
HeroNode resNode = binaryTree.preOrderSearch(5);
if(resNode!=null){
System.out.printf("找到了,信息为no=%d,name=%s\n",resNode.getNo(),resNode.getName());
}else {
System.out.printf("没有找到no=%d的英雄\n",resNode.getNo());
}
System.out.println("一共找了"+HeroNode.count+"次");
*/
System.out.println("中序遍历方式");
HeroNode resNode = binaryTree.infixOrderSearch(5);
if(resNode!=null){
System.out.printf("找到了,信息为no=%d,name=%s\n",resNode.getNo(),resNode.getName());
}else {
System.out.printf("没有找到no=%d的英雄\n",resNode.getNo());
}
System.out.println("一共找了"+HeroNode.count+"次");
}
}
//定义BinaryTree 二叉树
class BinaryTree{
private HeroNode root;
public void setRoot(HeroNode root) {
this.root = root;
}
public HeroNode getRoot() {
return root;
}
//前序遍历
public void preOrder(){
if(this.root!=null){
this.root.preOrder();
}else{
System.out.println("二叉树为空,无法遍历");
}
}
//中序遍历
public void infixOrder(){
if(this.root!=null){
this.root.infixOrder();
}else{
System.out.println("二叉树为空,无法遍历");
}
}
//后序遍历
public void postOrder(){
if(this.root!=null){
this.root.postOrder();
}else{
System.out.println("二叉树为空,无法遍历");
}
}
//前序遍历查找
public HeroNode preOrderSearch(int no){
if(root != null){
return this.root.preOrderSearch(no);
}else{
return null;
}
}
//中序遍历查找
public HeroNode infixOrderSearch(int no){
if(root != null){
return this.root.infixOrderSearch(no);
}else{
return null;
}
}
//后序遍历查找
public HeroNode postOrderSearch(int no){
if(root != null){
return this.root.postOrderSearch(no);
}else{
return null;
}
}
}
//创建HeroNode 节点
class HeroNode{
private int no;
private String name;
private HeroNode left;
private HeroNode right;
static int count = 0;
public HeroNode(int no, String name) {
this.no = no;
this.name = name;
}
public int getNo() {
return no;
}
public void setNo(int no) {
this.no = no;
}
public String getName() {
return name;
}
public void setName(String name) {
this.name = name;
}
public HeroNode getLeft() {
return left;
}
public void setLeft(HeroNode left) {
this.left = left;
}
public HeroNode getRight() {
return right;
}
public void setRight(HeroNode right) {
this.right = right;
}
@Override
public String toString() {
return "HeroNode{" +
"no=" + no +
", name='" + name + '\'' +
'}';
}
//编写前序遍历
public void preOrder(){
System.out.println(this); //先输出父节点
//递归向左子树前序遍历
if(this.left!=null){
this.left.preOrder();
}
if(this.right!=null){
this.right.preOrder();
}
}
//中序遍历
public void infixOrder(){
if(this.left!=null){
this.left.infixOrder();
}
//输出父节点
System.out.println(this);
if(this.right!=null){
this.right.infixOrder();
}
}
//后序遍历
public void postOrder(){
//向左子树递归
if(this.left!=null){
this.left.postOrder();
}
//向右子树递归
if(this.right!=null){
this.right.postOrder();
}
//输出父节点
System.out.println(this);
}
//前序遍历查找
/**
*
* @param no 查找的编号
* @return 找到就返回对应的英雄,没有就返回null
*/
public HeroNode preOrderSearch(int no) {
count++;
//比较当前节点
if (this.no == no) {
return this;
}
HeroNode resNode = null;
//向左子树递归
if (this.left != null) {
resNode = this.left.preOrderSearch(no);
}
if(resNode!=null){
return resNode;
}
//向右子树递归
if (this.right != null) {
resNode = this.right.preOrderSearch(no);
}
return resNode;
}
//中序遍历查找
public HeroNode infixOrderSearch(int no) {
HeroNode resNode = null;
//向左子树递归
if (this.left != null) {
resNode = this.left.infixOrderSearch(no);
}
if(resNode!=null){
return resNode;
}
count++;
//比较当前节点
if (this.no == no) {
return this;
}
//向右子树递归
if (this.right != null) {
resNode = this.right.infixOrderSearch(no);
}
return resNode;
}
//后序遍历
public HeroNode postOrderSearch(int no) {
HeroNode resNode = null;
//向左子树递归
if (this.left != null) {
resNode = this.left.postOrderSearch(no);
}
if(resNode!=null){
return resNode;
}
//向右子树递归
if (this.right != null) {
resNode = this.right.postOrderSearch(no);
}
if(resNode != null){
return resNode;
}
count++;
//比较当前节点
if (this.no == no) {
return this;
}
return null;
}
}
要分析查找的次数,count需要放在比较之前

如果放在前面可能只判断了左右是否为空,但是没有进行值的比较
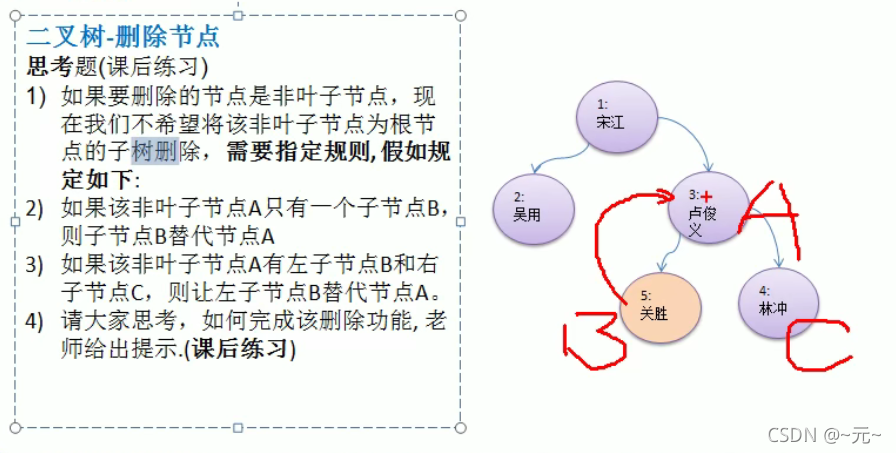
二叉树节点删除思路
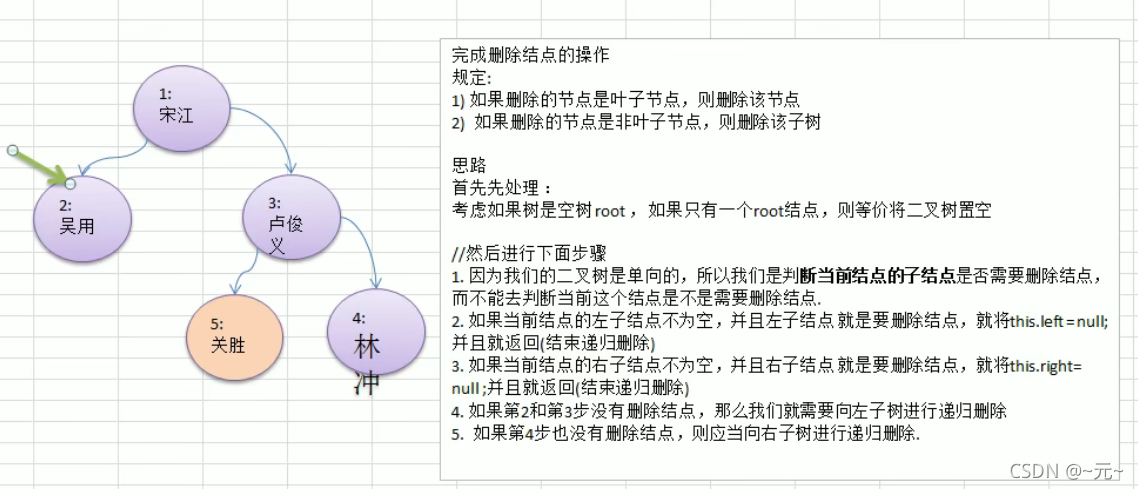
?
//递归删除节点
//1.如果删除的节点是叶子节点,则删除该节点
//2.如果是非叶子节点,则删除该子树
public void delNode(int no){
//判断左子节点
if(this.left != null && this.left.no == no){
this.left = null;
return;
}
//判断右子节点
if(this.right != null && this.right.no == no){
this.right = null;
return;
}
if(this.left!=null){
this.left.delNode(no);
}
if(this.right!=null){
this.right.delNode(no);
}
}?
顺序存储二叉树
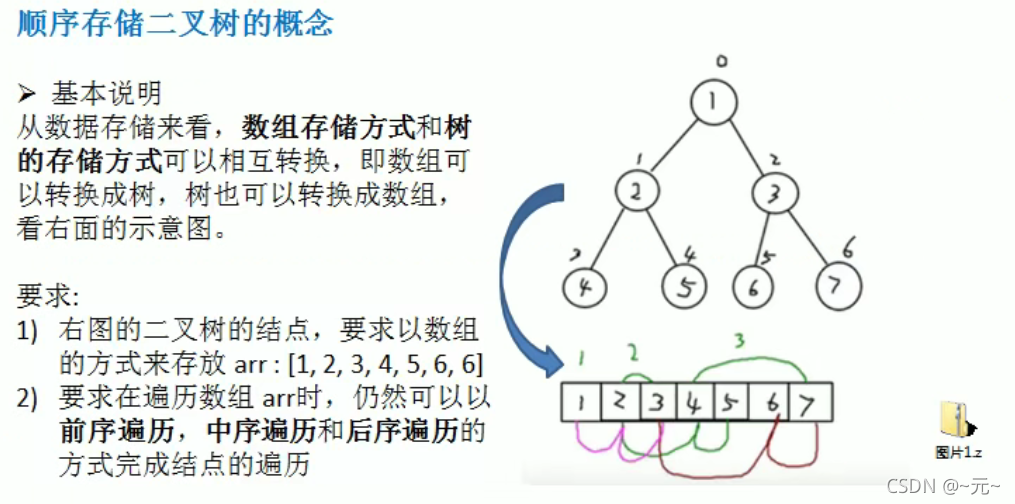

package com.atyuan.tree;
/**
* @program: DataStructures
* @description: 顺序存储二叉树
* @author: yuan
* @create: 2021-10-19 21:37
**/
public class ArrBinaryTreeDemo {
public static void main(String[] args) {
//模拟一个已经顺序存储好的数组 1 2 4 5 3 6 7
int[] arr = {1,2,3,4,5,6,7};
ArrBinaryTree arrBinaryTree = new ArrBinaryTree(arr);
arrBinaryTree.preOrder(0);
}
}
//课后作业中序后序
class ArrBinaryTree{
//存储数据节点的数组
private int[] arr;
public ArrBinaryTree(int[] arr){
this.arr = arr;
}
//顺序存储二叉树的前序遍历
/**
*
* @param index 数组下标索引
*/
public void preOrder(int index){
//如果数组为空,或者arr.length=0
if(arr == null || arr.length == 0){
System.out.println("数组为空,不能按照二叉树的前序遍历");
return;
}
//输出当前元素
System.out.print(arr[index]+"\t");
//向左递归遍历,且需要防止越界
if((index * 2 + 1) < arr.length){
preOrder(2 * index + 1);
}
//向右递归
if((index * 2 + 2) < arr.length){
preOrder(2 * index + 2);
}
}
}线索化二叉树

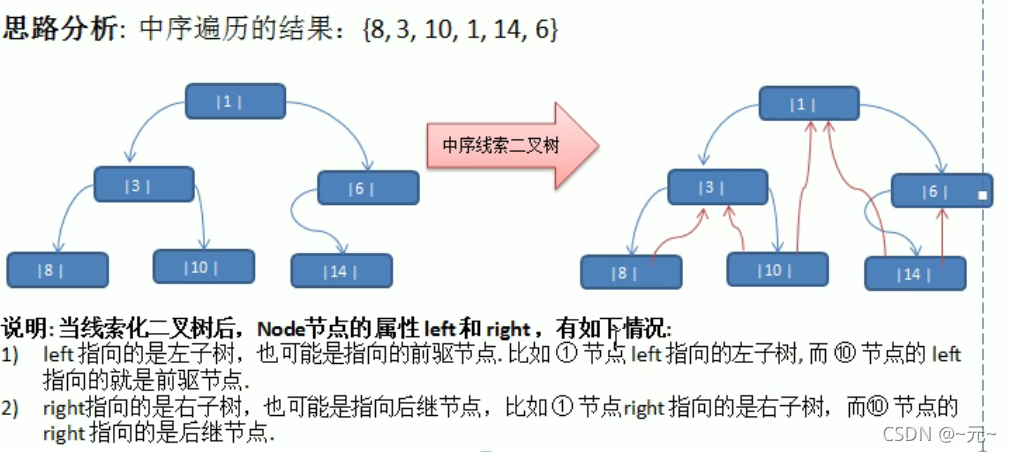
package com.atyuan.tree.threadedbinarytree;
/**
* @program: DataStructures
* @description: 线索化二叉树
* @author: yuan
* @create: 2021-10-19 22:06
**/
public class ThreadedBinaryTreeDemo {
public static void main(String[] args) {
//测试中序线索二叉树功能
HeroNode root = new HeroNode(1, "Tom");
HeroNode node2 = new HeroNode(3, "Jack");
HeroNode node3 = new HeroNode(6, "Mike");
HeroNode node4 = new HeroNode(8, "Mary");
HeroNode node5 = new HeroNode(10, "LiHua");
HeroNode node6 = new HeroNode(6, "HAHA");
root.setLeft(node2);
root.setRight(node3);
node2.setLeft(node4);
node2.setRight(node5);
node3.setLeft(node6);
//创建线索化二叉树
ThreadedBinaryTree threadedBinaryTree = new ThreadedBinaryTree();
threadedBinaryTree.setRoot(root);
//线索化
threadedBinaryTree.threadedNodes();
//查看已线索化的节点
HeroNode node5Right = node5.getRight();
System.out.println(node5Right);
threadedBinaryTree.threadedList();
}
}
class ThreadedBinaryTree{
private HeroNode root;
//创建指向当前节点的前驱节点的指针
private HeroNode pre = null;
public void setRoot(HeroNode root) {
this.root = root;
}
public HeroNode getRoot() {
return root;
}
public void threadedNodes(){
this.threadedNodes(root);
}
//遍历线索化二叉树
public void threadedList(){
HeroNode node = root;
while(node != null){
//循环找到LeftType == 1的节点,第一个找到的就是8,
// 后面随着遍历而变化,因为当leftType == 1时,说明该节点是按照线索化
//处理后的有效节点
while(node.getLeftType() == 0){
//如果等于0就接着往下遍历
node = node.getLeft();
}
//打印当前节点
System.out.println(node);
//如果当前节点的右指针指向的是后继节点,就一直输出
while(node.getRightType() == 1){
node = node.getRight();
System.out.println(node);
}
//替换这个遍历的节点,node变成null才可退出
node = node.getRight();
}
}
//编写对二叉树进行中序线索化的方法
/***
*
* @param node 当前要线索化的节点
*/
public void threadedNodes(HeroNode node){
//如果node为空,不能线索化
if(node == null){
return;
}
//先线索化左子树
threadedNodes(node.getLeft());
//线索化当前节点
//处理当前节点的前驱节点
if(node.getLeft() == null){
//第一个数左节点为空
node.setLeft(pre);
//修改当前节点的左指针类型,指向前驱节点
node.setLeftType(1);
}
//处理后继节点
if(pre != null && pre.getRight() == null){
//让前驱节点的右指针指向当前节点
pre.setRight(node);
//修改前驱节点的右指针类型
pre.setRightType(1);
}
pre = node;
//线索化右子树
threadedNodes(node.getRight());
}
//删除节点
public void delNode(int no){
if(this.root != null){
if(root.getNo() == no){
root = null;
}else{
//递归删除
root.delNode(no);
}
}
}
//前序遍历
public void preOrder(){
if(this.root!=null){
this.root.preOrder();
}else{
System.out.println("二叉树为空,无法遍历");
}
}
//中序遍历
public void infixOrder(){
if(this.root!=null){
this.root.infixOrder();
}else{
System.out.println("二叉树为空,无法遍历");
}
}
//后序遍历
public void postOrder(){
if(this.root!=null){
this.root.postOrder();
}else{
System.out.println("二叉树为空,无法遍历");
}
}
//前序遍历查找
public HeroNode preOrderSearch(int no){
if(root != null){
return this.root.preOrderSearch(no);
}else{
return null;
}
}
//中序遍历查找
public HeroNode infixOrderSearch(int no){
if(root != null){
return this.root.infixOrderSearch(no);
}else{
return null;
}
}
//后序遍历查找
public HeroNode postOrderSearch(int no){
if(root != null){
return this.root.postOrderSearch(no);
}else{
return null;
}
}
}
//创建HeroNode 节点
class HeroNode{
private int no;
private String name;
private HeroNode left;
private HeroNode right;
static int count = 0;
//如果leftType == 0 表示指向的是左子树,如果为1表示指向前驱节点
//如果rightType == 0 表示指向的是右子树,如果为1表示指向后继节点
private int leftType;
private int rightType;
public int getLeftType() {
return leftType;
}
public void setLeftType(int leftType) {
this.leftType = leftType;
}
public int getRightType() {
return rightType;
}
public void setRightType(int rightType) {
this.rightType = rightType;
}
public HeroNode(int no, String name) {
this.no = no;
this.name = name;
}
public int getNo() {
return no;
}
public void setNo(int no) {
this.no = no;
}
public String getName() {
return name;
}
public void setName(String name) {
this.name = name;
}
public HeroNode getLeft() {
return left;
}
public void setLeft(HeroNode left) {
this.left = left;
}
public HeroNode getRight() {
return right;
}
public void setRight(HeroNode right) {
this.right = right;
}
@Override
public String toString() {
return "HeroNode{" +
"no=" + no +
", name='" + name + '\'' +
'}';
}
//递归删除节点
//1.如果删除的节点是叶子节点,则删除该节点
//2.如果是非叶子节点,则删除该子树
public void delNode(int no){
//判断左子节点
if(this.left != null && this.left.no == no){
this.left = null;
return;
}
//判断右子节点
if(this.right != null && this.right.no == no){
this.right = null;
return;
}
if(this.left!=null){
this.left.delNode(no);
}
if(this.right!=null){
this.right.delNode(no);
}
}
//编写前序遍历
public void preOrder(){
System.out.println(this); //先输出父节点
//递归向左子树前序遍历
if(this.left!=null){
this.left.preOrder();
}
if(this.right!=null){
this.right.preOrder();
}
}
//中序遍历
public void infixOrder(){
if(this.left!=null){
this.left.infixOrder();
}
//输出父节点
System.out.println(this);
if(this.right!=null){
this.right.infixOrder();
}
}
//后序遍历
public void postOrder(){
//向左子树递归
if(this.left!=null){
this.left.postOrder();
}
//向右子树递归
if(this.right!=null){
this.right.postOrder();
}
//输出父节点
System.out.println(this);
}
//前序遍历查找
/**
*
* @param no 查找的编号
* @return 找到就返回对应的英雄,没有就返回null
*/
public HeroNode preOrderSearch(int no) {
count++;
//比较当前节点
if (this.no == no) {
return this;
}
HeroNode resNode = null;
//向左子树递归
if (this.left != null) {
resNode = this.left.preOrderSearch(no);
}
if(resNode!=null){
return resNode;
}
//向右子树递归
if (this.right != null) {
resNode = this.right.preOrderSearch(no);
}
return resNode;
}
//中序遍历查找
public HeroNode infixOrderSearch(int no) {
HeroNode resNode = null;
//向左子树递归
if (this.left != null) {
resNode = this.left.infixOrderSearch(no);
}
if(resNode!=null){
return resNode;
}
count++;
//比较当前节点
if (this.no == no) {
return this;
}
//向右子树递归
if (this.right != null) {
resNode = this.right.infixOrderSearch(no);
}
return resNode;
}
//后序遍历
public HeroNode postOrderSearch(int no) {
HeroNode resNode = null;
//向左子树递归
if (this.left != null) {
resNode = this.left.postOrderSearch(no);
}
if(resNode!=null){
return resNode;
}
//向右子树递归
if (this.right != null) {
resNode = this.right.postOrderSearch(no);
}
if(resNode != null){
return resNode;
}
count++;
//比较当前节点
if (this.no == no) {
return this;
}
return null;
}
}
堆排序
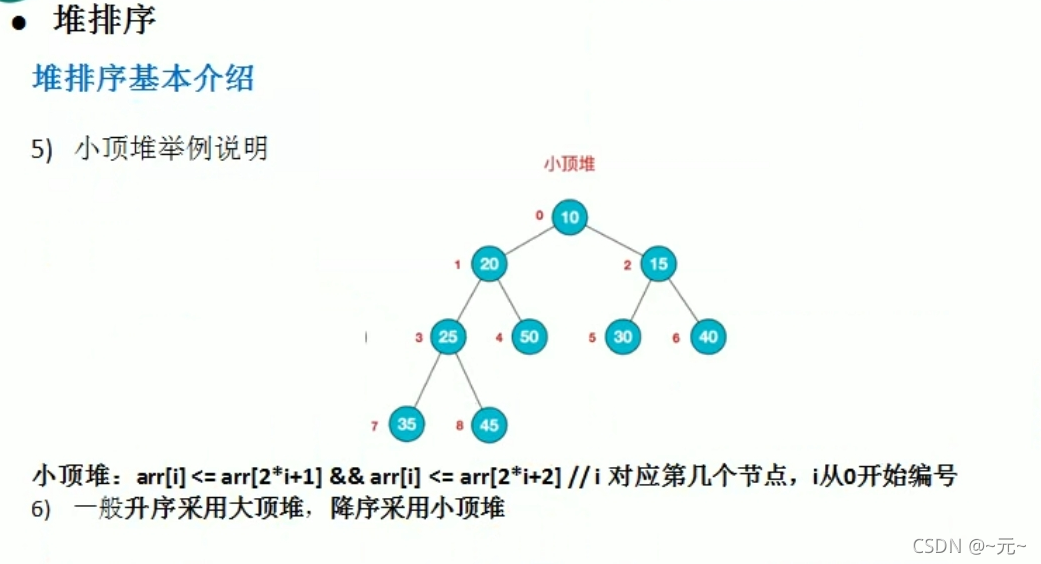
?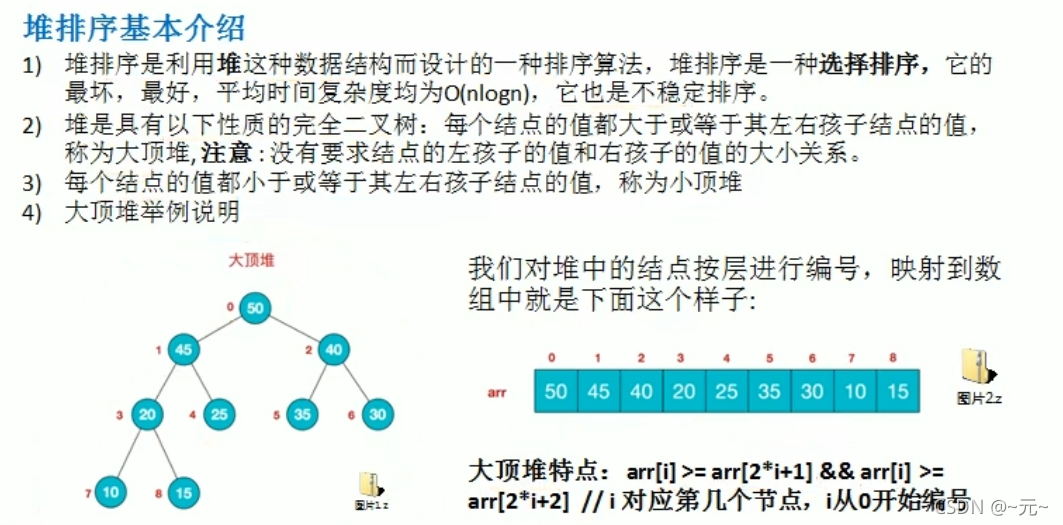
?
package com.atyuan.sort;
import java.util.Arrays;
/**
* @program: DataStructures
* @description: 堆排序
* @author: yuan
* @create: 2021-10-20 20:09
**/
public class HeapSort {
//升序使用大顶堆,降序使用小顶堆
public static void main(String[] args) {
int[] arr = {4,6,8,5,9};
heapSort(arr);
System.out.println(Arrays.toString(arr));
}
//编写堆排序的方法
public static void heapSort(int arr[]){
System.out.println("堆排序");
int temp = 0;
// 将无序序列构建成一个大顶堆
for (int i = arr.length / 2 - 1; i >= 0; i--) {
adjustHeap(arr,i, arr.length);
}
//将堆顶元素与末尾元素交换
for (int j = arr.length - 1; j > 0; j--) {
//交换
temp = arr[j];
arr[j] = arr[0];
arr[0] = temp;
adjustHeap(arr,0,j);
}
}
//调整成大顶堆
/**
* 功能:完成将以i对应的非叶子节点的数调整成大顶堆
* @param arr 待调整的数组
* @param i 表示非叶子节点在数组中的索引
* @param length 表示对多少个元素继续调整,length在逐渐减少
*/
public static void adjustHeap(int[] arr, int i,int length){
//保存当前元素的值,保存到临时变量
int temp = arr[i];
//k = 2 * i + 1:表示左子节点
for (int k = 2 * i + 1; k < length; k = k * 2 + 1 ) {
//说明左子节点的值
if(k+1 < length && arr[k] < arr[k+1]){
k++; //k指向右节点
}
if(arr[k] > temp){
arr[i] = arr[k]; //把较大的值赋给当前节点
i = k; //i指向k,继续循环比较
}else{
break;
}
}
//当for循环结束,已经将以i为父节点的树的最大值放到顶上
arr[i] = temp; //将原来的值放到替换的位置
}
}
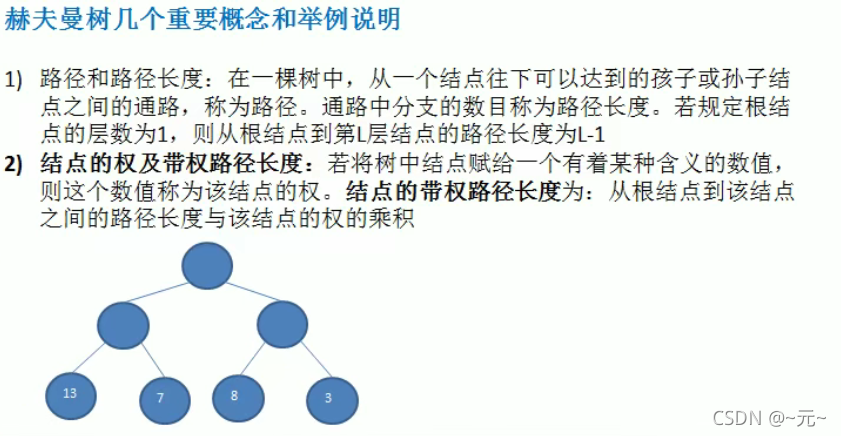
赫夫曼树

?
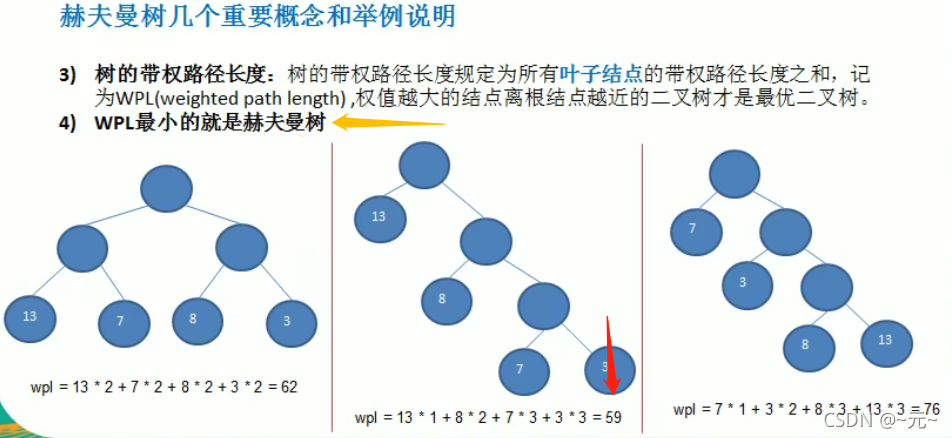

package com.atyuan.huffmanTree;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Collections;
import java.util.List;
/**
* @program: DataStructures
* @description: 赫夫曼树
* @author: yuan
* @create: 2021-10-20 21:57
**/
public class HuffmanTree {
public static void main(String[] args) {
int[] arr = {13,7,8,3,29,6,1};
Node huffmanTree = createHuffmanTree(arr);
preOrder(huffmanTree);
}
//编写前序遍历
public static void preOrder(Node root){
if(root!=null){
root.preOrder();
}else{
System.out.println("空树不能遍历");
}
}
//创建赫夫曼树的方法
public static Node createHuffmanTree(int[] arr){
//遍历arr数组
//将arr的每个元素构成一个Node
//将Node放入到ArrayList
List<Node> nodes = new ArrayList<>();
for (int value : arr) {
nodes.add(new Node(value));
}
while (nodes.size() > 1){
//从小到大排序
Collections.sort(nodes);
//取出权值最小的两个二叉树
Node leftNode = nodes.get(0);
Node rightNode = nodes.get(1);
//构建新的二叉树
Node parent = new Node(leftNode.value + rightNode.value);
parent.left = leftNode;
parent.right = rightNode;
//删除处理过的二叉树
nodes.remove(leftNode);
nodes.remove(rightNode);
//将parent加入到集合中
nodes.add(parent);
}
return nodes.get(0);
}
}
class Node implements Comparable<Node>{
int value; //结点权值
Node left; //指向左节点
Node right; //指向右结点
//前序遍历
public void preOrder(){
System.out.println(this);
if(this.left != null){
this.left.preOrder();
}
if(this.right != null){
this.right.preOrder();
}
}
public Node(int value){
this.value = value;
}
@Override
public String toString() {
return "Node{" +
"value=" + value +
'}';
}
@Override
public int compareTo(Node o) {
//从小到大排
return this.value - o.value;
}
}