内容
1.链表与邻接表
2.栈与队列
3.kmp
要非常快得 把代码默写出来 一个模板要好好儿理解于熟练
《记忆力和自制力》
一、链表
数组模拟构造 静态链表
1.单链表
#include<iostream>
//算法 不是工程 所以就可以不怕内存泄露
using namespace std;
//head 头节点的下标
//e[]值 ne[] 结点i的next指针 即i.next
//idx当前待插入的位置,即当前已经用到哪个点了
const int N = 100010;
int head,e[N],ne[N],idx;
//初始化 用-1 表示空 所以尾结点也是-1
void init(){
head = -1;
idx = 0;
}
//从头结点 插入指针
void head_add(int x){
e[idx] = x; //当前位置赋值;
ne[idx] = head;//当前位置的下一个结点 应该指向 之前头指针所指
head = idx;
idx++;
}
//在第k个位置后面 插入x
void add(int k,int x){
e[idx] = x,ne[idx] = ne[k],ne[k] = idx,idx++;
}
//删除k后面的点
void remove(int k){
ne[k] = ne[ne[k]];
}
int main(){
//主函数里写的
return 0;
}
//链表的遍历办法!!!
for(int i = head;i != -1;i = ne[i]){
cout<<e[i]<<" ";
}
2.双链表
常用来做某些问题的优化
int m;
const int N = 100010;
int e[N],l[N],r[N],idx;
//初始化
void init(){
//0 是左端点 1是右端点
r[0] = 1; //0号点的左边 是1号点
l[1] = 0;
idx = 2;
}
//在第k个插入的数后面右侧插入一个数
//在第k个点的左边插入 就是在l[k]的右边插入;
void add(int k,int x){
e[idx] = x;
r[idx] = r[k];
l[idx] = k;
l[r[k]] = idx;
r[k] = idx;
}
//删除第k个数
//左边的右边 直接等于右边
//右边的左边 直接等于左边
void remove(int k){
r[l[k]] = r[k];
l[r[k]] = l[k];
}
3.邻接表
就是n个 单链表
常,用来解决数和图的问题的。
二、栈和队列
1.栈
栈的操作要求

#include<iostream>
using namespace std;
const int N = 100010;
int stk[N],tt;
//插入
stk[++t]=x;
//删除
t--;
//判空
if(tt>0) notempty;
else empty
//栈顶元素
stk[tt];
2.队列
如图:
//队尾插入元素 队头弹出元素 tt是队尾
int q[N],hh = 0,tt=-1;
//插入
q[++t] = x;
//弹出
hh++;
//判空
if(hh<=tt) notempty;
else empty;
//取元素
q[hh];
单调栈和单调队列
(抽象但一共也没有几种题型)
用于优化

3.单调栈

//有逆序的关系 前面的数就删掉了
#include <iostream>
using namespace std;
const int N =100010;
int stk[N],tt;
//tt栈顶指针
int main(){
//ios::sync_with_stdio(false);
int n;
cin>>n;
for(int i = 0; i < n;i++){
int x;
scanf("%d",&x);
while(tt&&stk[tt]>=x) tt--;
//栈里面的元素大于当前元素 栈顶元素就没希望了
//如果 是找左边比他大的第一个数 那么栈顶元素比当前元素小 则没希望
if(tt) printf("%d ",stk[tt]);
else printf("-1 ");
stk[++tt] = x;
}
return 0;
}
变单调 再求极值 求极值的时间就是O(1)了
4. 单调队列
(题目:滑动窗口)
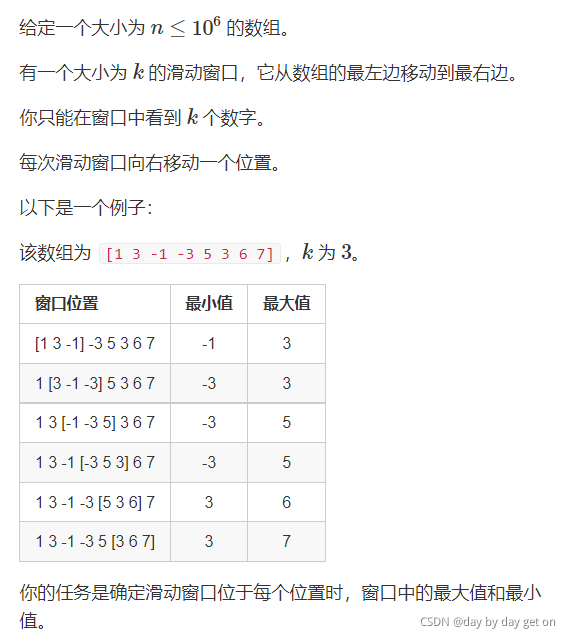
思路:
当求最小时,当i>j且a[i]>a[j],a[i]一定不作为答案出现,于是我们可以得到一个上升序列
#include<iostream>
using namespace std;
const int N =1000010;
//入队和出队
//因为是 在两边操作
//用队列 来存储下标
//多重背包 也可以用单调队列优化
int n,k;
int a[N],q[N];
int main(){
scanf("%d%d",&n,&k);
int hh = 0,tt = -1;
for(int i = 0; i < n; i++) scanf("%d",&a[i]);
//求最小值
for(int i = 0; i < n;i++){
if(hh<=tt&&q[hh] <= i-k) hh++;
while(hh<=tt&&a[q[tt]]>=a[i]) tt--; //循环的条件不为空 且有比当前大的数
//要注意! 必须要在有第k个的时候 才能输出
q[++tt] = i;
if(i >= k - 1) printf("%d ",a[q[hh]]);
}
puts("");
//求最大值
hh = 0, tt = -1; //一定要清空 队列
for(int i = 0; i < n; i++){
if(hh<= tt && q[hh] <= i-k) hh++;
while(hh <= tt && a[q[tt]] <= a[i]) tt--;
q[++tt] = i;
if(i >= k-1) printf("%d ",a[q[hh]]);
}
return 0;
}
总结:
共同思路都是,首先用模拟栈和队列暴力的做法做出来,然后观察有哪些元素是不需要的,删掉不需要的元素得到单调的序列,(挖掘一些性质、可以把目光集中到比较少的状态里面,从而减少复杂度)。
即:单调 再找极值
三、KMP
KMP算法是一种改进的字符串匹配算法
KMP是三位大牛:D.E.Knuth、J.H.Morris和V.R.Pratt同时发现的。其中第一位就是《计算机程序设计艺术》的作者!!
KMP算法要解决的问题就是在字符串(也叫主串)中的模式(pattern)定位问题。说简单点就是我们平时常说的关键字搜索。模式串就是关键字(接下来称它为P),如果它在一个主串(接下来称为T)中出现,就返回它的具体位置,否则返回-1(常用手段)。