[数据结构与算法]2021-10-18 剑指offer2：49~58题目+思路+多种题解

写在前面

本文是采用python为编程语言，作者自行练习使用，题目列表为：剑指 Offer（第 2 版），未使用实体书，难度未标注的均为“简单”，我也不是很清楚为什么有几个编号没有提供。“《剑指 Offer（第 2 版）》通行全球的程序员经典面试秘籍。剖析典型的编程面试题，系统整理基础知识、代码质量、解题思路、优化效率和综合能力这 5 个面试要点。”，本文中的思路来源于每道题目中的题解部分，争取提供全面，优化后的题解，其中所有代码已通过题目检验。

剑指 Offer 49. 丑数（中等）

题目

思路

• 动态规划：第一眼拿到挺懵的，感觉又是找规律的题，但是总不能让我们一个一个的去乘叭，遂列出了前20个丑数，诶，其实前面的丑数知道的情况下，分别乘以2，3，5不就是啦。但是会发现过程中存在很多重复，也是这个题的难点！
  • 如何取到最接近的数？其实就是取一个最小值，那么很自然的会想到下一问
  • 取谁的最小值呐？在我们的理想情况下，我们期望取到的是刚刚比dp[当前]恰好大的几个数且要覆盖最后一个乘数因子是2，3，5的情况（因为无法用贪心思想直接判断究竟最后乘哪一个因子最小），于是我们想维护3个指针，分别指向乘上这三个因子最接近dp[当前]的前一个数
  • 怎么找到这样的数？对之前的丑数循环遍历，分别乘这三个因子肯定是能找到的，但是冗余操作在于如果这个数找的偏小，那它就应该被排到（即就是当前dp的最小值）；如果找的偏大，那排了之后的几个数仍然应该是这个数，所以维护的指针不用动。
• 最小堆：实际上还是动态规划，不过利用堆排序。需要维护一个hash表进行重复判定，堆操作的复杂度是O(logn)，优于排序的列表。但会有大量的重复计算。

题解

class Solution:
    def nthUglyNumber(self, n: int) -> int:
        dp, a, b, c = [1] * n, 0, 0, 0
        for index in range(1, n):
            n2, n3, n5 = dp[a] * 2, dp[b] * 3, dp[c] * 5
            dp[index] = min(n2, n3, n5)
            # 使用if都判断一遍的原因是：
                # 可能会出现重复的数字，如2*3和3*2都是6，它们的指针都该往后挪啦
            # 一个一个指针挪但不会存在冗余的原因是：
                # 需要取遍所有的数，但是如果出现重复的话，同一时间总会指向相同的“最小值”
            if dp[index] == n2: a += 1
            if dp[index] == n3: b += 1
            if dp[index] == n5: c += 1
        return dp[-1]
        

• 最小堆：

class Solution:
    def nthUglyNumber(self, n: int) -> int:
        factors = [2, 3, 5]
        seen = {1}
        heap = [1]

        for i in range(n - 1):
            curr = heapq.heappop(heap)
            for factor in factors:
                if (nxt := curr * factor) not in seen:
                    seen.add(nxt)
                    heapq.heappush(heap, nxt)

        return heapq.heappop(heap)

作者：LeetCode-Solution
链接：https://leetcode-cn.com/problems/chou-shu-lcof/solution/chou-shu-by-leetcode-solution-0e5i/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

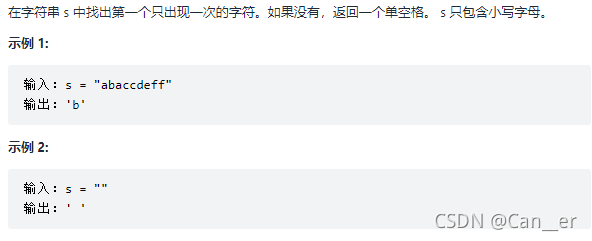
剑指 Offer 50. 第一个只出现一次的字符

题目

思路

统计次数，然后遍历一遍取出符合条件的，其中有两点可以减少复杂度：

• 如果是短字符串，遍历哈希表不如遍历字符串快；反之长字符串，遍历字符串不如遍历哈希表快。
• python中默认字典有序，使用bool记录结果更省空间

题解

class Solution:
    def firstUniqChar(self, s: str) -> str:
        dic = {}
        for c in s:
            dic[c] = not c in dic
        for k, v in dic.items():
            if v: return k
        return ' '
        

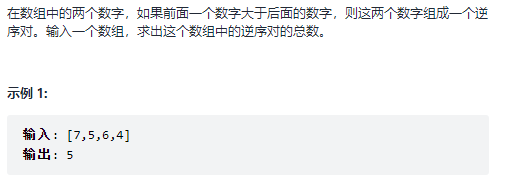
剑指 Offer 51. 数组中的逆序对（困难）

题目

思路

“如果之前没有接触过这类题，将这个题作为入手记住是一个不错的选择。”这道题目共有两个思路：

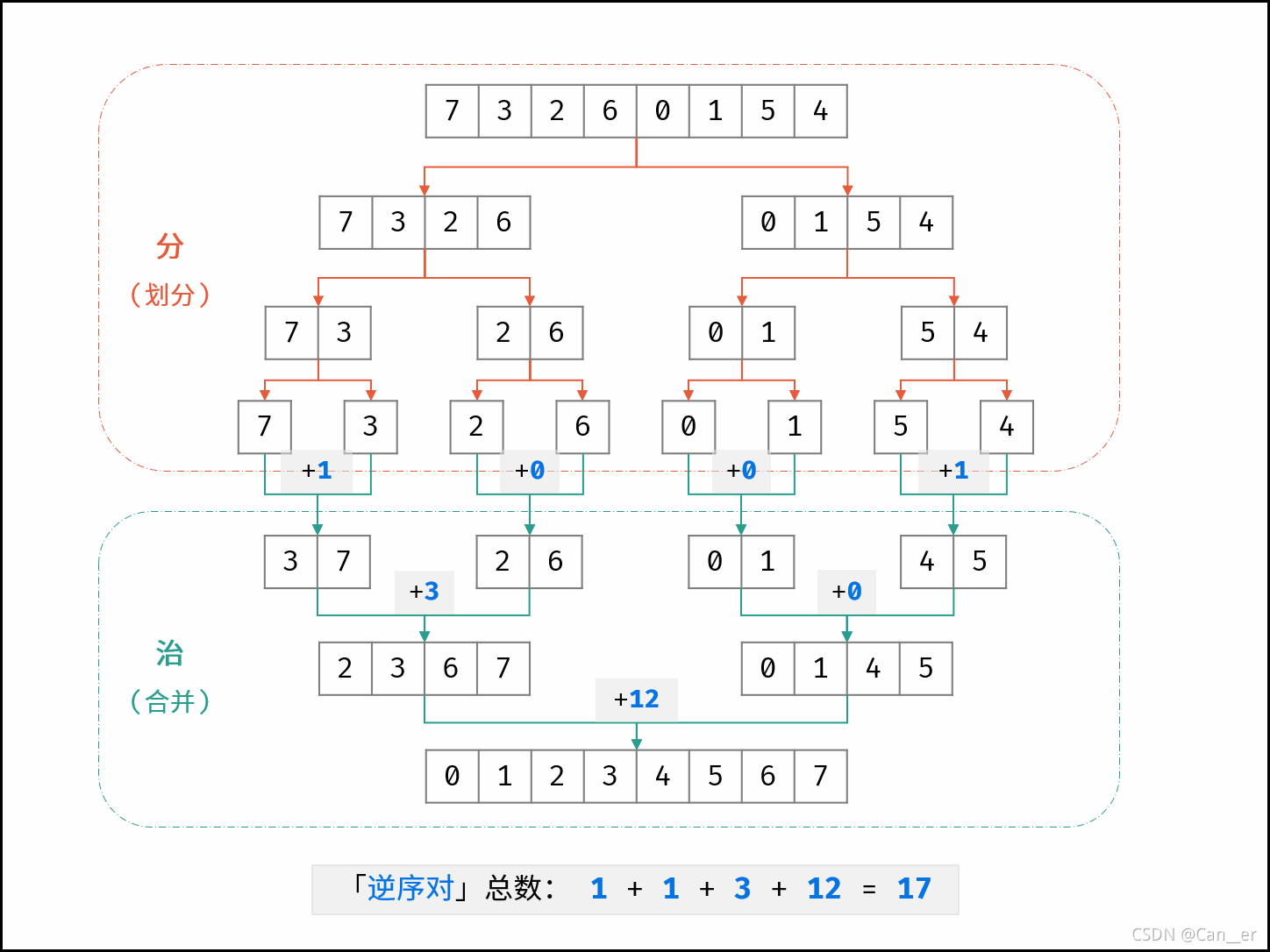
• 归并排序：利用了“部分有序数组”的逆序数可以直接算出其逆序数，即将数组递归的划分成“左 右”两个部分，在将右部分数组中元素放到前面归并的过程，如果左侧有n个元素，说明该右侧的数造成的逆序数为n。以此合并下去，每次合并是对“组内”的合并，下次就是相对这次的“组间”逆序数的计算，看图：
  
• 离散化树状数组：
  • 离散化一个序列的前提是我们只关心这个序列里面元素的相对大小，而不关心绝对大小（即只关心元素在序列中的排名）；离散化的目的是让原来分布零散的值聚集到一起，减少空间浪费。那么如何获得元素排名呢，我们可以对原序列排序后去重，对于每一个 a_i通过二分查找的方式计算排名作为离散化之后的值。
  • 倒序遍历数组，将出现的值的桶加1，所有在它前面的（即小于其）的桶之和即为逆序数，因为这些值本该在其前面，却已经被遍历了。

题解

• 归并排序：

class Solution:
    def reversePairs(self, nums: List[int]) -> int:
        def merge_sort(l, r):
            # 终止条件
            if l >= r: 
                return 0
            # 递归划分
            m = (l + r) // 2
            res = merge_sort(l, m) + merge_sort(m + 1, r)
            # 合并阶段
            i, j = l, m + 1
            tmp[l:r + 1] = nums[l:r + 1]
            for k in range(l, r + 1):
                if i == m + 1:
                    # 左边取完了
                    nums[k] = tmp[j]
                    j += 1
                elif j == r + 1 or tmp[i] <= tmp[j]:
                    # 右边取完了或者左边小于右边
                    nums[k] = tmp[i]
                    i += 1
                else:
                    # tmp[i] > tmp[j], 逆序对
                    nums[k] = tmp[j]
                    j += 1
                    res += m - i + 1 # 统计逆序对
            return res
        
        tmp = [0] * len(nums)
        return merge_sort(0, len(nums) - 1)
                

• 离散化树状数组：

    def reversePairs(self, nums) -> int:
        temp = []
        res = 0
        for t in reversed(nums):
            # bisect是python内置模块，用于有序序列的插入和查找。返回的值是应该插入的位置。
            curr = bisect.bisect_left(temp, t)
            # 因为是从后向前遍历，所以插入的位置的下标就是逆序数（前面有n个比自己小但是原数组中排在自己后面的）
            res += curr
            # list不能直接插入，但是可以用切片的方法
            temp[curr:curr] = [t]
        return res

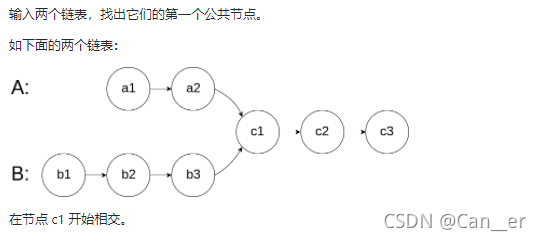
剑指 Offer 52. 两个链表的第一个公共节点

题目

思路

• 比较好想到的一个思路就是将A中的每个元素拿出来，遍历B比较，但是这样复杂度太差啦
• 另一个想法是这样的，走的快的结点等一等走的慢的，或者说，走的快的结点早点开始，而这个早的度就是 非公共序列短的部分，诶那我们循环一遍统计出短多少，然后让短的链表等长的链表这个长度就好了
• 换句话说，长的链表在第一遍没走完的时候，短的链表已经开始结束了，那我在长的链表在走的过程中，我从头开始走长的链表，等长链表结束后来走短链表，这样我们一定一起结尾（也是题意表达的相同后缀），也一定能碰到相同元素（如果有的话）

题解

class Solution:
    def getIntersectionNode(self, headA: ListNode, headB: ListNode) -> ListNode:
        A, B = headA, headB
        while A != B:
            if not A:
                A = headB
            else:
                A = A.next
            if not B:
                B = headA
            else:
                B = B.next
        return A
        

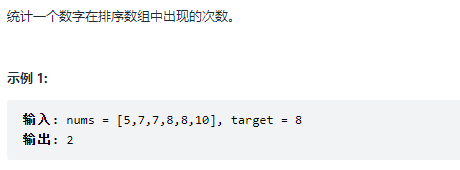
剑指 Offer 53 - I. 在排序数组中查找数字 I

题目

思路

排好序了…二分是不二之选，但因为返回的是个数嘛，所以需要找两边，分别通过相等的时候往右取or往左取来找到right和left

题解

• 二分法未改进版：

class Solution:
    def search(self, nums: List[int], target: int) -> int:
        l, l_, r, r_ = 0, 0, len(nums)-1, len(nums)-1
        while l <= r:
            med = (l+r)//2
            if nums[med]<target:
                l = med+1
            else: r = med-1
        if not nums or l>=len(nums) or nums[l] !=target: return 0
        while l_<= r_:
            med_ = (l_+r_)//2
            if nums[med_]<=target:
                l_ = med_+1
            else: r_ = med_-1
        return r_-l+1

• K神的二分法改进版：“本质上看， helper() 函数旨在查找数字 tartar 在数组 nums 中的 插入点 ，且若数组中存在值相同的元素，则插入到这些元素的右边。”

class Solution:
    def search(self, nums: [int], target: int) -> int:
        def helper(tar):
            i, j = 0, len(nums) - 1
            while i <= j:
                m = (i + j) // 2
                if nums[m] <= tar: i = m + 1
                else: j = m - 1
            return i
        return helper(target) - helper(target - 1)

作者：jyd
链接：https://leetcode-cn.com/problems/zai-pai-xu-shu-zu-zhong-cha-zhao-shu-zi-lcof/solution/mian-shi-ti-53-i-zai-pai-xu-shu-zu-zhong-cha-zha-5/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

剑指 Offer 53 - II. 0～n-1中缺失的数字

题目

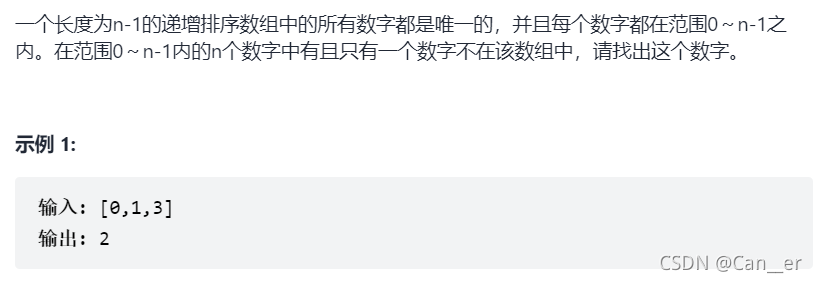
思路

• 排序中查找，还是二分哈哈这几个题都好简单🤪

题解

class Solution:
    def missingNumber(self, nums: List[int]) -> int:
        l, r = 0, len(nums)-1
        # 加上等号是为了一个元素的情况，避免0，0提前退出循环
        while l<=r:
            med = (l+r)//2
            if nums[med]==med:
                l += 1
            else: r-=1
        return l

剑指 Offer 54. 二叉搜索树的第k大节点

题目

思路

实际上就是给一个排序二叉树，我们需要先排序（中序遍历即可），但因为寻找的是从大到小的第k个，所以我们采用“右-中-左”的方法进行递归，同时注意两点：

• 剪枝：当检查到了符合条件的，直接层层return，而没必要再继续
• 使用类变量：否则会出现重复计算（传入函数的值在栈中单独存储）情况，且返回bool而不是值更省

题解

class Solution:
    def kthLargest(self, root: TreeNode, k: int) -> int:
        self.k = k
        def dfs(root):
            if not root:
                return
            r_v = dfs(root.right)
            if r_v:
                return r_v
            self.k-=1
            if self.k==0:
                self.res = root.val
                return True
            l_v = dfs(root.left)
            if l_v:
                return l_v
        dfs(root)
        return self.res

剑指 Offer 55 - I. 二叉树的深度

题目

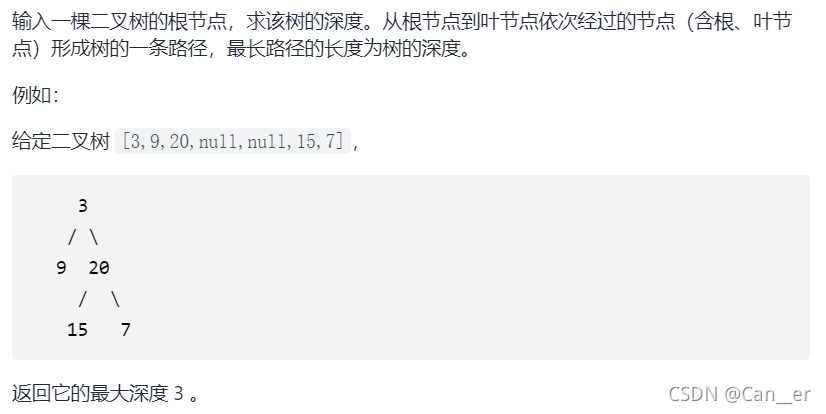
思路

DFS和BFS的反复练习…

• 其中传统的dfs往往有两种实现方式，一个是递归，下面的解答已经很清晰啦。另一种就是迭代，其实迭代特别像广度优先，但是借助的是栈，之所以存入元组（包含长度信息），是因为栈中存储的是所有访问过的结点，而不是dfs的某一条路,每层加入的个数不同，也并不知道从哪里开始出现了分叉（或回退到哪一步），用在这个题效果出乎意料的好哈哈哈。
• BFS的魅力在于队列中存的一直是某一层的元素！

题解

• 递归DFS：

class Solution:
    def maxDepth(self, root: TreeNode) -> int:
        if not root: return 0
        return max(self.maxDepth(root.left), self.maxDepth(root.right)) + 1

• 迭代DFS：头一回自己第一遍就写出这么牛的效果，贴个图，太开心啦
  

class Solution:
    def maxDepth(self, root: TreeNode) -> int:
        dep, stack, maxdep = 0, [], 0
        if root: stack.append((root, 1))
        while stack:
            node, lenth = stack.pop()
            if node.left: stack.append((node.left, lenth+1))
            if node.right: stack.append((node.right, lenth+1))
            # 到叶结点时进行比较
            elif lenth> maxdep:
                maxdep =lenth
        return maxdep

• BFS

class Solution:
    def maxDepth(self, root: TreeNode) -> int:
        if not root: return 0
        queue, res = [root], 0
        while queue:
            tmp = []
            for node in queue:
                if node.left: tmp.append(node.left)
                if node.right: tmp.append(node.right)
            queue = tmp
            res += 1
        return res

剑指 Offer 55 - II. 平衡二叉树

题目

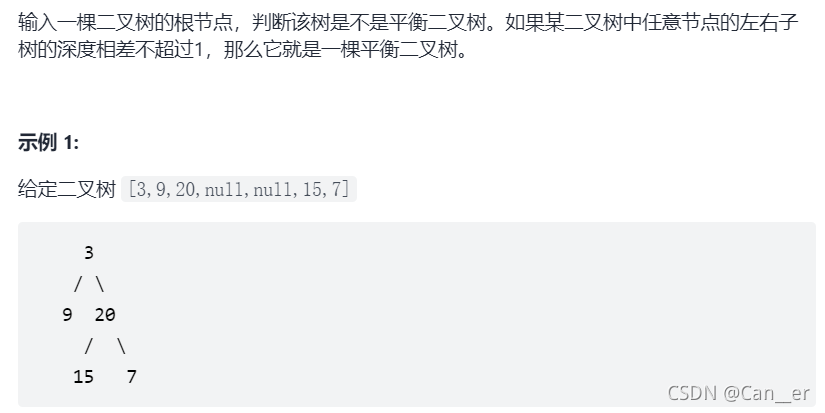
思路

想用递归的方法返回bool值，来判断是否是平衡二叉树，但是这样就需要再进行重复计算来递归的计算深度，所以这种“不满足条件”和“返回深度”双重功能的，考虑使用if条件，如果不满足则返回-1，否则返回深度，以便上一层递归。

题解

class Solution:
    def isBalanced(self, root: TreeNode) -> bool:
        def dfs(root):
            if not root: return 0
            left = dfs(root.left)
            # 一旦有一个不满足条件，立即返回
            if left == -1: return -1
            right = dfs(root.right)
            if right == -1: return -1
            return max(left, right) + 1 if abs(left - right) <= 1 else -1

        return dfs(root) != -1

剑指 Offer 56 - I. 数组中数字出现的次数（中等）

题目

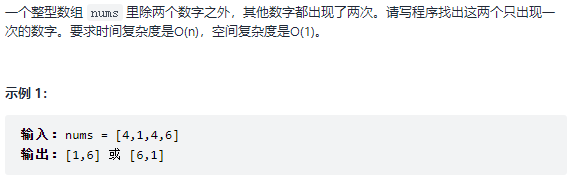
思路

空间复杂度为O(1)，首先就排除了这类题常用的循环遍历和哈希表，考虑位运算，因为出现两次的数字经过异或（不同为1）操作后都为0，所以剩下的为1的数字一定满足是这两个只出现一次的数字，且该位不同的位，那么要想求这两个数字，考虑将数字分成两组，满足：1. 这两组分别包含这两个数字 2. 相同的数字会被分到相同的组中

• 先遍历所有数字进行异或，得出一个含0和1的位
• 找到任意一个位为1的位，按这个位对数字进行划分（相同的数字在该位一定相同）
• 分别对这两组进行亦或操作，最后的结果就是这两个单独的数

题解

class Solution:
    def singleNumbers(self, nums: List[int]) -> List[int]:
        res = functools.reduce(lambda x,y: x^y, nums)
        bit = 1
        while bit & res ==0:
            bit <<= 1
        num1, num2 = 0, 0
        for num in nums:
            if num & bit: num1 ^=num
            else: num2 ^= num
        return [num1, num2]

剑指 Offer 56 - II. 数组中数字出现的次数 II（中等）

题目

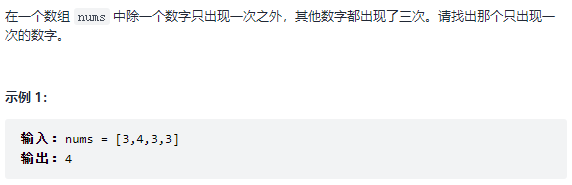
思路

承接上题，考察的仍是位运算，但是因为该题中的其它数字出现了3次，所以我们期望的位运算有这样的性质：当是0的时候累加变成1，是1的时候累加变成2，是2的时候累加重新变成0。所以目的是使用两个二进制位表示3个状态，很自然得出这两个变量需要遵循 00 -> 01 -> 10这样的变化规律，用high和low表示这两位，n表示当前是0或1，上代码

low = low^n & ~high
high = high^n & ~low

至于这个公式是怎么来的，可以参考下图，发现相比位运算的low^n而言，新运算的low位只有在high=1的时候发生了改变，即1变0了，那我们根据high的变化，为保证其它结果不变，与上一个非high即可。

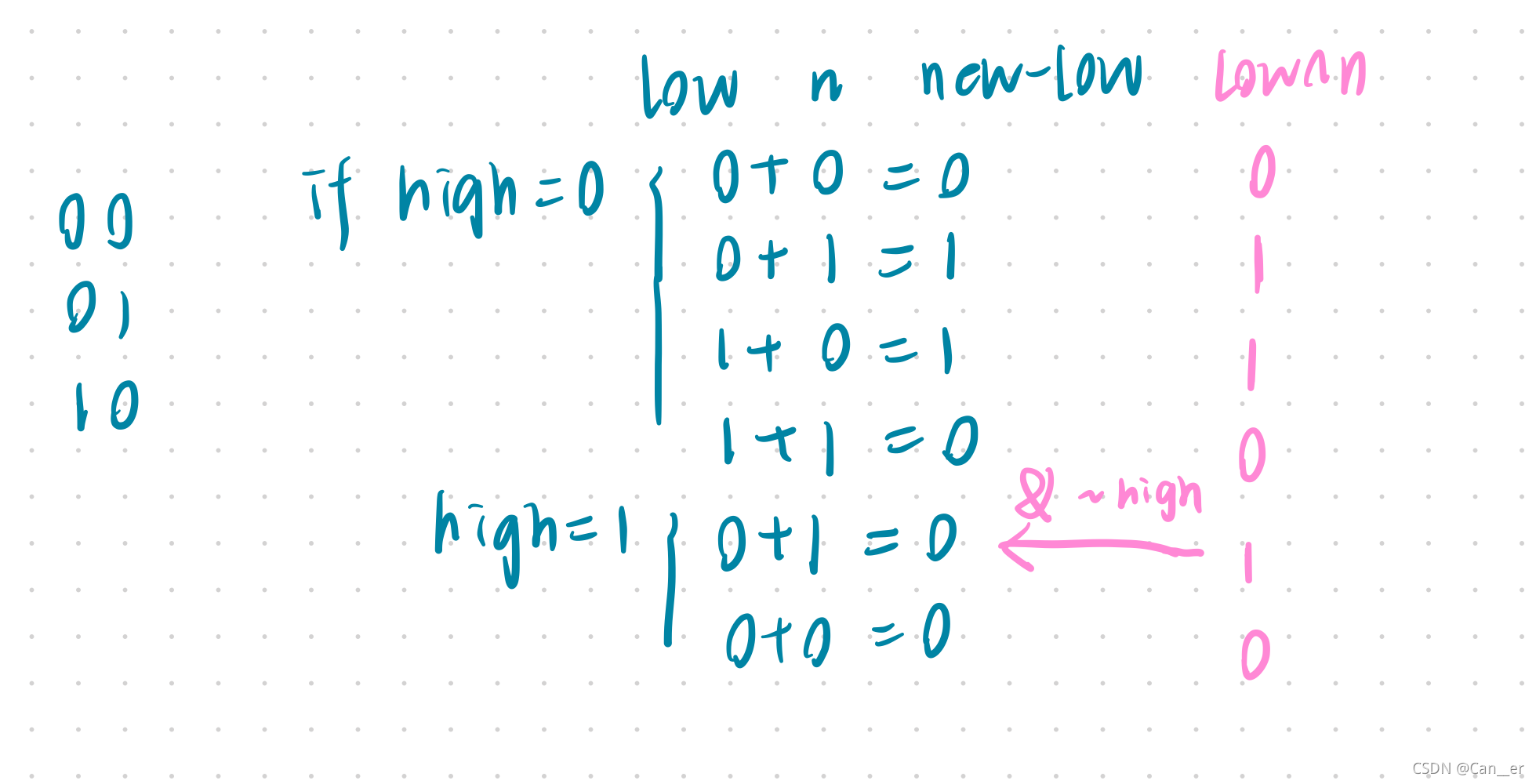
题解

class Solution:
    def singleNumber(self, nums: List[int]) -> int:
        low, high = 0, 0
        # 针对整个数而不是某一位而言，可将high视作一个辅助数字，用于辅助low的变化
        # 让其满足0，1，0的变化规律
        for num in nums:
            low = low ^ num & ~high
            high = high ^ num & ~low
        # 对于00 01 10来说 代表着真正的出现的1次的位数实际上是low
        return low

剑指 Offer 57. 和为s的两个数字

题目

分析

• 二分查找：因为有序，实际上就是遍历每个元素，再使用二分查找target-num[now]，其中如果要找的数已经小于当前的数，停止搜索
• 哈希表：利用哈希表存储元素及其是否出现，当扫描到后面的元素时，前面的元素已经能在哈希表中取到
• 双指针：一个从左至右，另一个从右至左，如果求和大了，右边的左移；求和小了，左边的右移。

题解

• 二分查找：

class Solution:
    def twoSum(self, nums: List[int], target: int) -> List[int]:
        # 只需要从当前索引 
        def bi_find(l, r, tar):
            while l< r:
                med = (l+r)//2
                if nums[med]==tar:
                    return True
                elif nums[med]>tar:
                    r = med-1
                else: l =med+1
            # 有可能指向同一元素时已经退出
            return nums[l]==tar
            
        for index in range(0,len(nums)):
            num = nums[index]
            print(index,len(nums),target-num)
            # 只需要检查index+1到最后一个元素即可
            if target-num>0 and bi_find(index+1,len(nums)-1,target-num):
                return num, target-num
        return

• 哈希表：

class Solution:
    def twoSum(self, nums: List[int], target: int) -> List[int]:
        numset=set()
        for num in nums:
            if target-num in numset:
                return num, target-num
            else: numset.add(num)
        return

• 双指针

class Solution:
    def twoSum(self, nums: List[int], target: int) -> List[int]:
        l, r = 0, len(nums) - 1
        while l < r:
            sum = nums[l] + nums[r]
            if sum > target: r -= 1
            elif sum < target: l += 1
            else: return nums[l], nums[r]
        return []

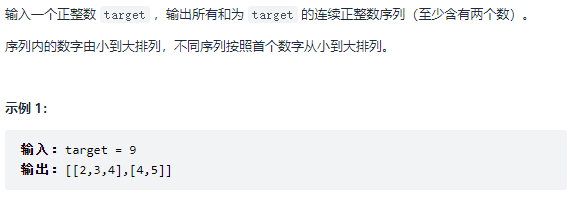
剑指 Offer 57 - II. 和为s的连续正数序列

题目

思路

• 第一反应是动态规划（实际上就是枚举），但是再一想，排好序的岂不是滑动窗口！
• 数学公式：从等差数列的求和公式（（首项+末项）*项数/2）推导过来，得到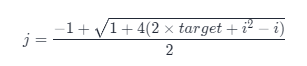
  其中j为非负数且大于i，同时j为整数！找到满足条件的就可以了。

题解

• 滑动窗口：

class Solution:
    def findContinuousSequence(self, target: int):
        l, r, res = 1, 2, []
        while l < r:
            # 使用求和公式实际上不如直接用sum对i和j操作快
            sum = (l+r)*(r-l+1)/2
            if sum == target:
                res.append(list(range(l, r+1)))
            # 相等的情况为了继续滑动
            if sum >= target:
                l = l+1
            else: r = r+1
        return res

• 数学方法：

class Solution:
    def findContinuousSequence(self, target: int):
        l, r, res = 1, 2, []
        while l < r:
            r = (-1 + (1 + 4 * (2 * target + l ** 2 - l)) ** 0.5) / 2
            if l < r and r == int(r):
                res.append(list(range(l, int(r) + 1)))
            l += 1
        return res

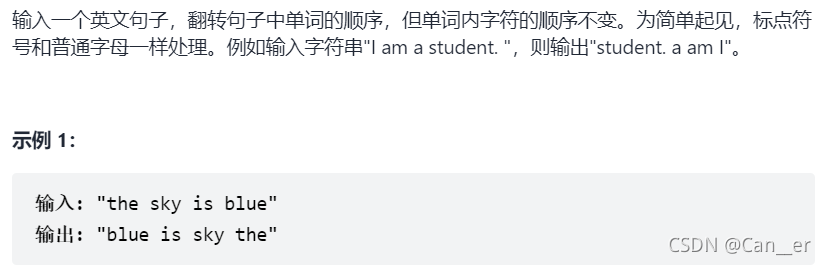
剑指 Offer 58 - I. 翻转单词顺序

题目

思路

不使用库函数，那就遍历一遍进行分析。因为是倒序输出，所以我们直接倒序遍历即可，遍历规则也很简单：

• 先删除首位空格
• 不是空格时，继续倒序，直到碰到空格停止，此时将单词加入列表；是空格时继续倒序，退出循环时将右指针指向当前位置
• 最后拼接返回即可

题解

class Solution:
    def reverseWords(self, s: str) -> str:
        s = s.strip()
        left = right = len(s) - 1
        res = []
        while left >= 0:
            while s[left] != ' ' and left >= 0: 
                left -= 1
            res.append(s[left + 1: right + 1])
            while s[left] == ' ': 
                left -= 1 
            right = left
        return ' '.join(res)

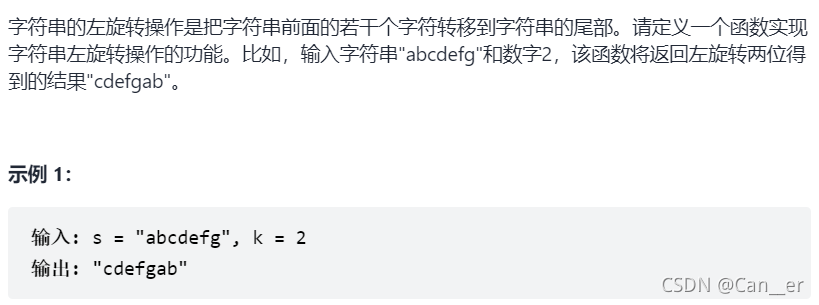
剑指 Offer 58 - II. 左旋转字符串

题目

思路

经典题目，考察的是“不要一位一位的挪动，而是从大局方向入手”：题目说的是旋转，实际上观察结果和原字符串会发现，就是将旋转的位数个字母拼接到了后面，那么直接使用切片即可。另外，有时会要求不能使用切片or列表（列表可伸缩无须重复申请内存空间肯定更好），那就字符串拼接，利用取余简化代码！

题解

• 直接切片：

class Solution:
    def reverseLeftWords(self, s: str, n: int) -> str:
        return s[n:] + s[:n]

• 字符串拼接：

class Solution:
    def reverseLeftWords(self, s: str, n: int) -> str:
        res = ""
        for _ in range(n, len(s) + n):
            res += s[_ % len(s)]
        return res