方法一:动态规划
要统计最长的有效括号。
一般这种题目就要求最长,最优的可以考虑用动态规划来做。基本可以保证时间复杂度在O(n)。
因为DP可以利用前面的状态方程的结果,而不会造成重复运算。
DP最关键的是找出问题与状态转移方程。
对于本题而言,要求最长的的有效括号()。
问题:从0到n之间,最长有效括号子字符串的长度。
而,求一个括号字符串的长度,要包括,
当前检测到的有效长度+
内部的括号的有效连续的括号字符串的长度+
前面的最长有效连续的括号字符串的长度
状态转移方程:f(n)=2+f(n-1)+f(外部)
当然,我们需要一共数组来保存之前的子结果,然后放入状态转移方程。
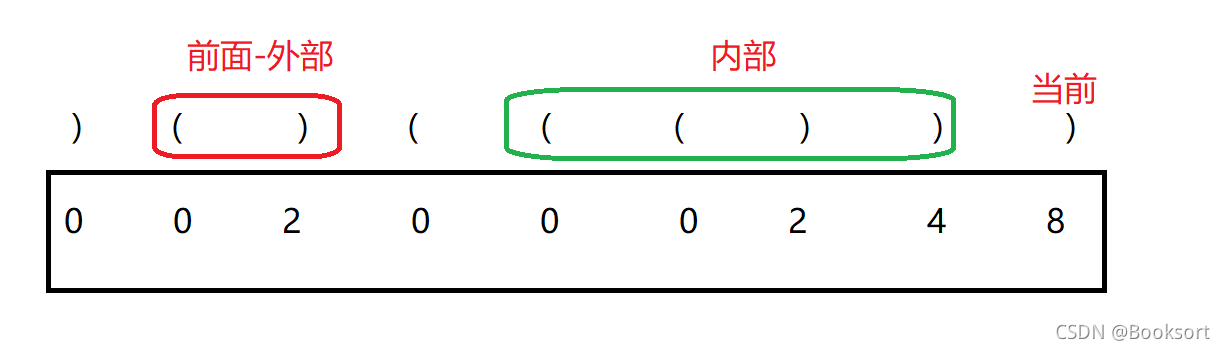
第一个元素无论是上面,数组保存到都是0。
如果元素是(,则数组保存的是0,因为这是找连续有效的字符串,如果数组保存到是到目前为止,数组中的最长有效子串,则会导致,有一些无效元素也会被统计进来,这样是不合适的。
如果这确实是一个有效字串,则当前的前一个元素一定是非0的值。说明相邻的子串都是有效的。
如果想要找到当前的最长有效子串,则前提条件的保证当前遍历的)一定有一个与之唯一匹配的(,而为了找到,要借助可能存在的内部的最长有效子串。如果内部有,则说明这个有效子串是可行的,可被统计的,如果内部没有,则说明内部是0,或者内部就不是有效的。

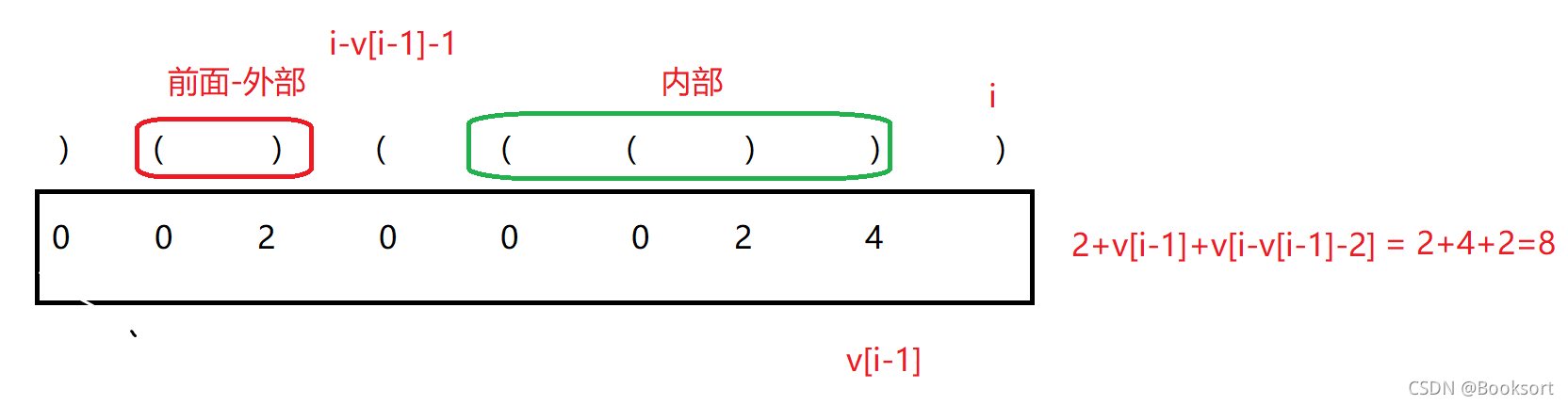
代码
class Solution {
public:
int longestValidParentheses(string s) {
if(s.empty())
return 0;
int len=s.size();
vector<int> v(len);
v.push_back(0);
for(int i=1;i<len;i++)
{
if(s[i]==')'&&((i-v[i-1]-1)>=0?s[i-v[i-1]-1]=='(':false))
v[i]=v[i-1]+2+((i-v[i-1]-2)>=0?v[i-v[i-1]-2]:0);
else
v[i]=0;
}
int Max=0;
for(int j=0;j<v.size();j++)
{
Max=max(v[j],Max);
}
return Max;
}
};
时间复杂度O(n),空间复杂度O(n)
方法二:正逆向相结合
这种方法适用于元素匹配的情况
- 先从0遍历到size()-1
- 再从size()-1遍历到0
先过一遍这个算法的过程,再介绍这个算法处理的特殊测试用例。

如果遍历到(,left就加一
如果遍历到),right就加1
什么时候代表有匹配的括号串?
当right和left一样时,说明统计到了匹配的括号串,其长度就需要加2。
如果right>left
说明)已经多于(,到目前的遍历来看,已经不符合有效字符串,则据目前为止,这次统计最长有效括号串已经到此为止,需要从0开始向后统计,则left与right需要重新置0。
当然,这并不能完全处理所有的测试用例
如果,是这种测试用例呢?

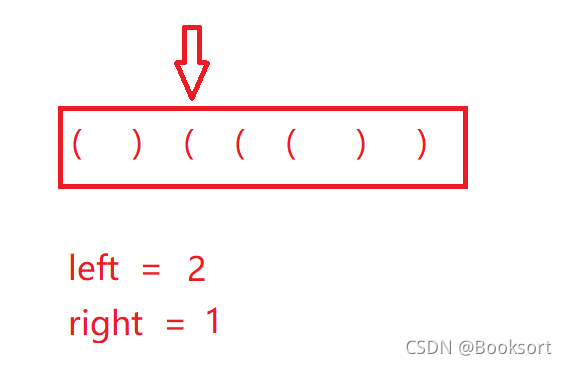
往后统计,则right就再也无法不能大于或等于left,而这种情况,后面是无法统计最长子串。所以就需要反向遍历一次,以保证,整个字符串的数据统计的正确性。
因为,作为一个(),理论上,无论是从左往右还是从右往左都是能得到一样的统计数据。
所以本题,使用正反两次遍历是为了验证数据的正确性。
class Solution {
public:
int longestValidParentheses(string s) {
int left=0;
int right=0;
int len=s.size();
int max_len=0;
for(int i=0;i<len;i++)
{
if(s[i]=='(')
left++;
if(s[i]==')')
right++;
if(left<right)
{
left=0;
right=0;
}
if(left==right)
{
int l=left*2;
max_len=max(l,max_len);
}
}
left=0;right=0;
for(int i=len-1;i>=0;i--)
{
if(s[i]=='(')
left++;
if(s[i]==')')
right++;
if(left>right)
{
left=0;
right=0;
}
if(left==right)
{
int l=left*2;
max_len=max(l,max_len);
}
}
return max_len;
}
};
时间复杂度O(n),空间复杂度O(1)