[数据结构与算法]模拟散列表 (开放寻址法)

思路

一个函数可以将一个范围内的数（本题为10^-9~10⁹）映射到另一个范围内(本题为0 ~ 10⁵)之间的一个数，被称为哈希函数。

1. 哈希函数的写法： x mod 10⁵；
   x取余后必然会在 0 ~ 10⁵之间。
2. 冲突
   可能会将若干不一样的数，映射到同一个数，（x范围大，值域范围小）大概率会发生冲突，如假设对12取余h[2] = 2， h[14] = 2;

开放寻址法和拉链法为对冲突的两种处理方法。

离散化是一种特殊的哈希方式

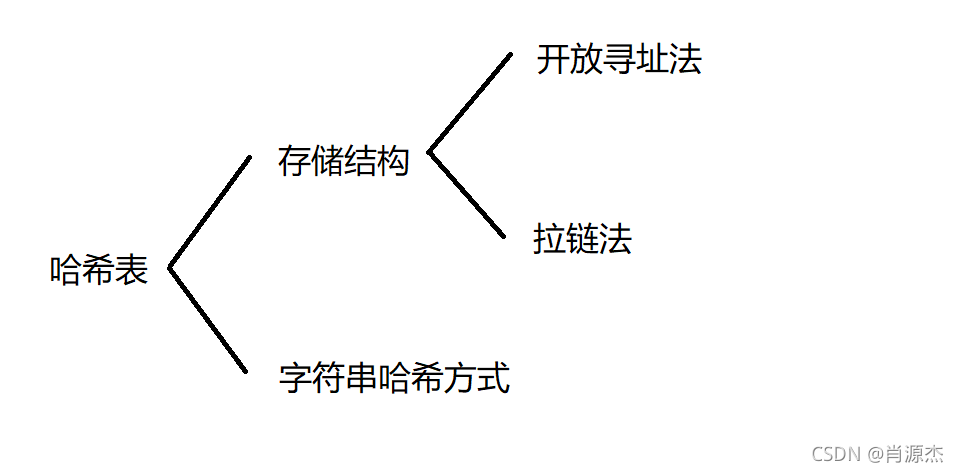
开放寻址法：

处理冲突的基本思路是创建一个一维数组，数组长度经验来说一般为题目操作数N的2~3倍，N表示总共需要存储的数的个数，本题而言，N最大为10⁵,所以这里数组的容量至少开到为2*10⁵。

对哈希函数而言，一般来说模的这个数，要取成质数，且这个质数要离2的整次幂尽可能的远，数学上可证明这么取的话冲突的概率是最小的。

以下算法来判断大于200000的第一个质数

判断最大质数

#include<iostream>
#include<cstring>
//判断100000以上第一个质数
using namespace std;

const int N = 200010;

int main() {
    for (int i = 200000; ; i++) {
        bool flag = true;
        for (int j = 2; j * j <= i; j++) {
            if (i % j == 0) {
                flag = false;
                break;
            }
        }
        if (flag){
            cout << i << endl;
            break;
        }
    }
    return 0;
}

结果输出为 200003;
故之后取数组长度为N = 200003。

插入的方法均从第k个数开始询问该位置是否有元素，有则k++，最终停留在没有元素的位置。
查找也一样，从第k个数开始询问这个位置存的数是否等于x。

int find(int x) {
    int k = (x % N + N) % N; //若x是负数时，可用该方法避免下标k出现负值，
    while (h[k] != null && h[k] != x) {
        k ++;
        if (k == N) k = 0;
    }//最终k停留的地方为等于x或null处
    return k;
}

我们在初始化h[N]以后要对其进行赋空null，以示此时没有元素插入，一般链表用-1，在此处，我们使用0x3f3f3f3f,来填充h[N]。宏定义null = 0x3f3f3f3f可以减少考虑时间：

引用一段他人博客中的介绍：

0x3f3f3f3f是一个很有用的数值，它是满足以下两个条件的最大整数。
1、整数的两倍不超过 0x7f7f7f7f，即int能表示的最大正整数。
2、整数的每8位（每个字节）都是相同的。
我们在程序设计中经常需要使用 memset(a, val, sizeof a) 初始化一个数组a，该语句把数值 val（0x00~0xFF）填充到数组a 的每个字节上，所以用memset只能赋值出“每8位都相同”的 int。
当需要把一个数组中的数值初始化成正无穷时，为了避免加法算术上溢出或者繁琐的判断，我们经常用 memset(a, 0x3f, sizeof(a)) 给数组赋 0x3f3f3f3f的值来代替。
（参考：https://blog.csdn.net/qq_31267769/article/details/88890612）

代码

#include<iostream>
#include<cstring>

using namespace std;

const int N = 200003, null = 0x3f3f3f3f;
int h[N];


int find(int x) {
    int k = (x % N + N) % N;
    while (h[k] != null && h[k] != x) {
        k ++;
        if (k == N) k = 0;
    }
    return k;
}

int main() {
    int n;
    scanf ("%d", &n); 
    memset(h, 0x3f, sizeof h); //填充h[N]
    while (n--) {
        char op[2];
        int x;
        
        scanf("%s%d",op, &x);
        int k = find(x);
        if (op[0] == 'I') h[k] = x;
        else {

            if (h[k] != null) puts("Yes");
            else puts("No");
        }
    }
    
    return 0;
}