本题在LeetCode官方评定难度为Hard,本文将较为详细的阐述该题的解法和步骤。
前言
本题是一道动态规划的典型题目,典型在其具有比普通的动态规划更强的技巧性。
若有不足,请联系补充;若有错误,请不吝指正。
一、题目描述


二、解题思路
1.题干提取
提取题干精华,可知:’ . ‘可以匹配任意一个字符,’ * ’ 可以让之前的那个字符重复任意次数,包括零次。
举例:
- " . a*b “可以匹配” zaaab "
- " a . .b “可以匹配” amnb "
- " . * " 可以匹配任意字符
2.思路分析
对于字符串 s 和 p 的匹配,大致过程是,用两个指针分别在 s 和 p 上移动,如果两个指针都能移动到字符串末尾,那么就匹配成功,否则,不成功。
思考之后发现,其实本题最难之处在于,字符" * "的处理,因为不管是普通字符还是 " . “字符,无非就是一对一的进行匹配,结果只有成功与失败而已,所以,处理好” * "字符,就能解决掉本题。
- 假设不考虑" * "字符
如果不考虑" * "字符,那么对于两个将要匹配的字符 s[ i ] 和 p[ j ],仅仅匹配和不匹配两种情况。
此时的代码:
bool isMatch(string s,string p)
{
int i=0,j=0;
while(i <s.size() && j <p.size()){
if(s[i]==p[j] || p[j]==' . '){
i++;
j++;
}else{
return false;
}
}
return i==j;
}
- 考虑" * "字符
加入" * “字符之后,我们需要考虑” * “字符的前一个字符在匹配时的情况:
当p[ j+1 ]为” * " 字符时,可以分为以下情况:
- 如果s[ i ]==p[ j ],那么有:
- p[ j ]匹配多个字符,比如s=" aaa “,p=” a* ",那么p[ 0 ]会通过 " * "匹配3个字符 " a "
- p[ j ]匹配 0 个字符,比如s=" aa “,p=” a*aa ",此时p[ 0 ]匹配 0 个字符
- 如果 s[ i ] != p[ j ],那么只有一种情况,p[ j ]只能匹配 0次,然后看下一个字符是否能与s[ i ]匹配,比如:s=" aa “,p=” b*aa ",此时p[ 0 ]只能匹配 0 次。
- 设置DP函数
根据上面的描述,我们设定 dp 函数的含义为:若dp(s ,i ,p ,j)=true,则表示 s[i…]可以匹配p[j…],若dp(s ,i ,p ,j)=false,则无法匹配,那么我们只需要得出 i=0, j=0时的结果即可。
代码实现:
bool dp(string & s,int i,string& p,int j){
if (s[i]==p[j] || p[j]==' . '){
if(j< p.size()-1 && p[ j+1]==" * "){
//情况一
return dp(s, i, p, j+2) || dp(s, i+1, p, i);}
else{
//情况二
return dp(s,i+1,p, j+1);
}
}else{
if(j<p.size()-1 && p[j+1]==' * '){
//情况三
return dp(s, i, p, j+2);}
else{
//情况四
return false;
}
}
}
3.解题步骤
对上文代码中各情况进行详细阐述:
情况一:
将 j 加2,i 不变,含义就是直接跳过p[ j ]和之后的通配符,即通配符匹配 0 次:
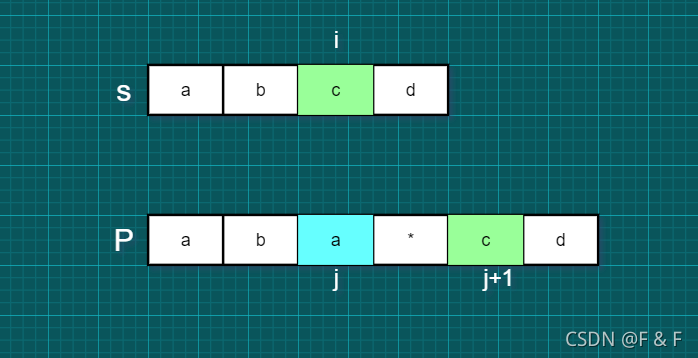
将 i 加1,j 不变,含义就是p[ j ]匹配了s[ i ],但p[ j ]还可以继续匹配,即通配符匹配多次:
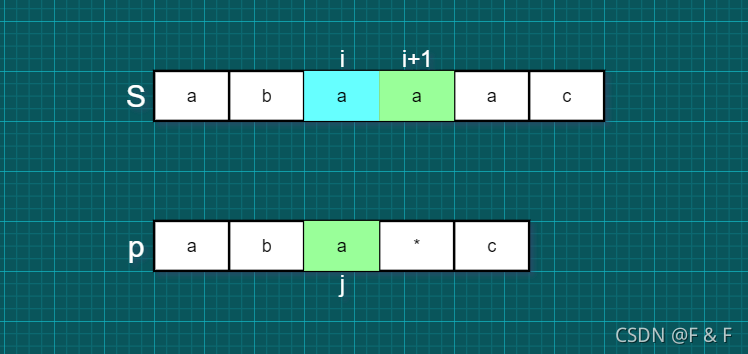
情况二:
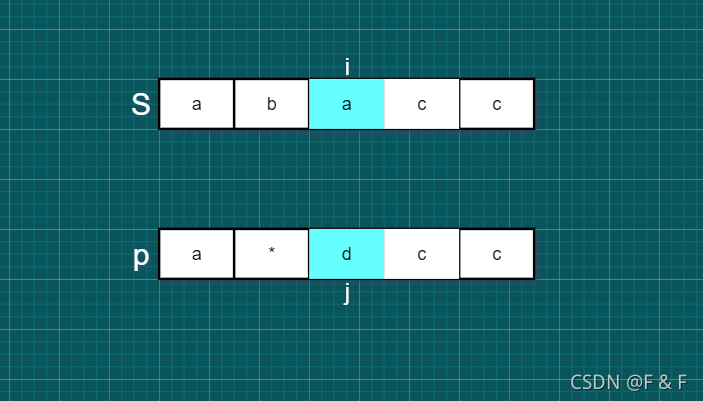
由于这个条件的分支是无 " * "的常规匹配,那么如果s[ i ]==p[ j ],就是 i 和 j 分别加1:
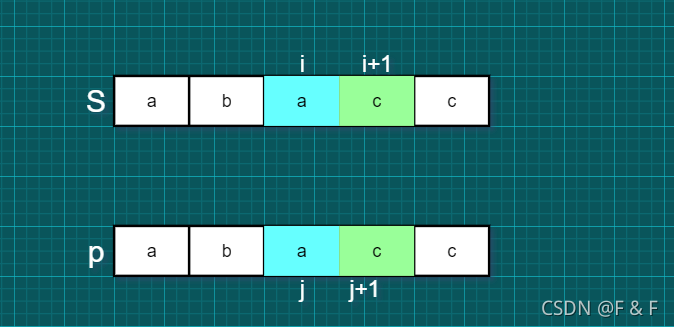
情况三:
将 j 加2,i 不变:
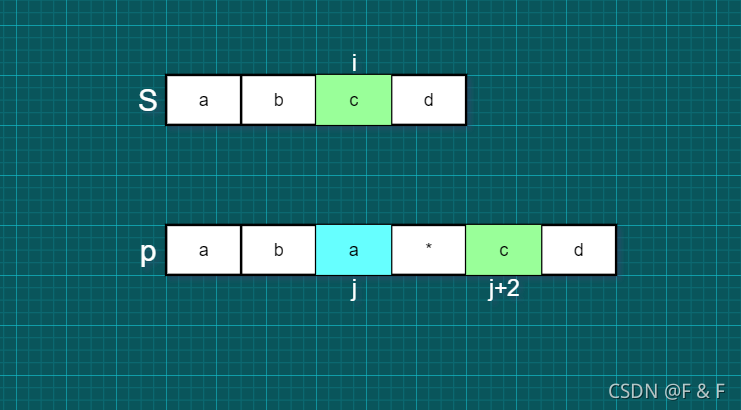
情况四:
如果没有" * "字符,也无法完成匹配,那么就匹配失败:
三、代码实现
python代码:代码地址
class Solution:
def isMatch(self, s: str, p: str):
if not p: return not s
if not s and len(p) == 1: return False
m = len(s) + 1
n = len(p) + 1
dp = [[False for _ in range(n)] for _ in range(m)]
dp[0][0] = True
# 确定dp数组的第一行,如果遇到了*,只要判断其对应的前面两个元素的dp值
# 注意:我们无需判断p里面的第一个值是否为"*",如果为"*",那肯定匹配不到为Fasle,原数组正好是Fasle,所以直接从2开始判断即可
for j in range(2, n):
if p[j-1] == '*':
dp[0][j] = dp[0][j - 2]
for r in range(1, m):
i = r - 1 # 对应s中的元素
for c in range(1, n):
j = c - 1 # 对应p中的元素
if s[i] == p[j] or p[j] == '.':
dp[r][c] = dp[r - 1][c - 1]
elif p[j] == '*':
if p[j - 1] == s[i] or p[j - 1] == '.':
dp[r][c] = dp[r - 1][c] or dp[r][c - 2]
else:
dp[r][c] = dp[r][c - 2]
else:
dp[r][c] = False
return dp[m - 1][n - 1]
java代码:代码地址
class Solution {
public boolean isMatch(String s, String p) {
if (p==null){
if (s==null){
return true;
}else{
return false;
}
}
if (s==null && p.length()==1){
return false;
}
int m = s.length()+1;
int n = p.length()+1;
boolean[][]dp = new boolean[m][n];
dp[0][0] = true;
for (int j=2;j<n;j++){
if (p.charAt(j-1)=='*'){
dp[0][j] = dp[0][j-2];
}
}
for (int r=1;r<m;r++){
int i = r-1;
for (int c=1;c<n;c++){
int j = c-1;
if (s.charAt(i)==p.charAt(j) || p.charAt(j)=='.'){
dp[r][c] = dp[r-1][c-1];
}else if (p.charAt(j)=='*'){
if (p.charAt(j-1)==s.charAt(i) || p.charAt(j-1)=='.'){
dp[r][c] = dp[r-1][c] || dp[r][c-2];
}else{
dp[r][c] = dp[r][c-2];
}
}else{
dp[r][c] = false;
}
}
}
return dp[m-1][n-1];
}
}
C++代码:代码地址
class Solution {
public:
bool isMatch(string s, string p) {
int m = s.size();
int n = p.size();
auto matches = [&](int i, int j) {
if (i == 0) {
return false;
}
if (p[j - 1] == '.') {
return true;
}
return s[i - 1] == p[j - 1];
};
vector<vector<int>> f(m + 1, vector<int>(n + 1));
f[0][0] = true;
for (int i = 0; i <= m; ++i) {
for (int j = 1; j <= n; ++j) {
if (p[j - 1] == '*') {
f[i][j] |= f[i][j - 2];
if (matches(i, j - 1)) {
f[i][j] |= f[i - 1][j];
}
}
else {
if (matches(i, j)) {
f[i][j] |= f[i - 1][j - 1];
}
}
}
}
return f[m][n];
}
};
C语言代码:代码地址
bool isMatch(char * s, char * p){
if (!*p) return !*s;
bool first_match = *s && (*s == *p || *p == '.');
if (*(p+1) == '*') {
return isMatch(s, p+2) || (first_match && isMatch(++s, p));
}
else {
return first_match && isMatch(++s, ++p);
}
}
总结
本题较为典型,但是难度也很典型,希望本文能帮到大家。
最后送大家一句话:再坚持一下,你的理想与热爱不应止步于此。